Edit this page

Algorithm Algorithm: KMP, Boyer-Moore, Rabin-Karp

Algorithm: KMP, Boyer-Moore, Rabin-Karp

Intro to Substring Search

N 길이의 텍스트에서 M 길이의 패턴을 찾는 문제다. 일반적으로 N >> M 이다. N 이 좀 많이 (무한히) 길기 때문에 지난시간까지 배운 알고리즘을 적용하기가 좀 힘들다.

(1) suffix sort 를 쓰려고 보니 suffixes 를 만드는 것 자체가 어렵다. 따라서 manber-myers MSD 도 패스.

(2) R-way 든 Ternary 든 tries 자체를 만들기 어렵다. 탐색해야 할 문서는 어마어마하기 때문에 메모리의 양이 모자랄 수 밖에 없다.

뭔가 문서를 streaming 취급하면서 처리할 수 있는 알고리즘이 필요하다.

주된 application 은

computer forensics: search memory, disk for signatures
CTRL + F
spam filtering: 특정 패턴이 발견되면 스팸이라 볼 수 있다.
internet traffic monitoring: 보안
screen scraping: 관련있는 패턴을 추출할 수 있다.

자바에서는 indexOf 메소드가 문자열에서 해당 패턴을 발견해 시작 인덱스를 돌려준다.

Brute Force

~~언젠가 양자 컴퓨터가 나오면 쓸모 있을까~~

public static int bruteForce(String pattern, String docs) {	
	int M = pattern.length();
	int N = docs.length();
	
	for (int i = 0; i < N - M; i ++) {
		int j;
		
		for (j = 0; j < M; j++) 
			if (pattern.charAt(j) != docs.charAt(i + j)) break;
			
		if (j == M) return i;
	}
	
	return N;
}

성능은 worst case 에서 ~M N 번의 char compares 가 필요하다. 예를 들어 문서가 AAAAAAAAAAAB 고 패턴이 AAAAAB 면 최악이다.

Backup

대부분의 application 에서 backup 하길 원치 않는다. 서론에 언급했듯이 스트림처럼 취급하고싶은데, brute force 에서는 backup 이 필요하기 때문에 last M characters 의 버퍼를 유지한다거나의 방법을 쓸 수 있다.

아래의 구현은 똑같은 비교 회수를 가지는데, backup 한다는걸 확실히 보여준다.

i points to end of sequence of already-matched chars in docs
j stores # of already-matched chars (end of sequence in pattern)

public static int bruteForceBackup(String pattern, String docs) {
	int i, N = docs.length();
	int j, M = pattern.length();
	
	for (i = 0, j = 0; i < N && j < M; i++) 
		if (docs.charAt(i) == pattern.charAt(j)) j++;
		else { i -= j; j = 0; }
	
	if (j == M) return i - M;
	else return N;
}

이게 M 이 작으면 문제가 안되는데, M 이 크면 문제가 될 수 있다.

우리가 풀어야 할 문제는

(1) linear-tme guarantee 가 필요
(2) backup 하지 않기

Knuth-Morris-Pratt

아이디어는 간단하다. 매칭에 실패했을 경우, 현재까지 처리한 문자들에 대한 정보 를 가지고 있기 때문에, 이걸 이용해서 필요 없는 부분을 건너 뛴다.

// pattern: BAAAAAAAAA

A B A A A A B A A A A A A A A A
  B A A A A ^ // fail
            B // ignore previous chars

DFA

Knuth-Morris-Pratt 알고리즘은 deterministic finite state automation, DFA 란 것에 이론적으로 기반한다.

DFA 는 abstract string-searching machine 이다.

Finite number of states (including start and halt)
Exactly one transition for each char in alphabet
Accept if sequence of transitions leads to half state

(http://www-igm.univ-mlv.fr)

더 크게 보면 DFA 는 Finite State Machine, FSM 의 한 종류다. DFA 말고도 Nondeterministic Finite Automata, NFA 가 있는데, 차이점은 이렇다.

비결정적 유한 오토마타는 결정적 유한 오토마타와는 다르게 입력 기호에 대해서 \epsilon-transition 에 의해 0개 이상의 이동이 가능하다. 만약 가능한 다음 상태의 경우가 없다면, 기계는 입력을 거부한다.

결정적 유한 오토마타는 입력값에 대해 출력 값이 1개라는 소리 같은데, 좀 모호해서 더 찾아봤다. 여기 에 의하면

Each input to a DFA or NFA affects the state of the automaton: if it was in state q immediately before the input, either it will be in some state q′ after the input, or the input will cause it to choke. (Note that q′ may be the same as q.) Suppose that we have an automaton in a state q. The difference in behavior between a DFA and an NFA is this:

If it’s a DFA, each possible input determines the resulting state q′ uniquely. Every input causes a state change, and the new state is completely determined by the input. Moreover, the automaton can change state only after reading an input.

If it’s an NFA, some inputs may allow a choice of resulting states, and some may cause the automaton to choke, because there is no new state corresponding to that input. Moreover, the automaton may be constructed so that it can change state to some new state q′ without reading any input at all.

As a consequence of this difference in behavior, DFA’s and NFA’s differ in another very important respect.

If you start a DFA in its initial state and input some word w, the state q in which the DFA ends up is completely determined by w: inputting w to the DFA will always cause it to end up in state q. This is what is meant by calling it deterministic.

If you start an NFA in its initial state and input some word w, there may be several possible states in which it can end up, since some of the inputs along the way may have allowed a choice of state changes. Consequently, you can’t predict from w alone in exactly which state the automaton will finish; this is what is meant by calling it nondeterministic. (And it’s actually a little worse than I’ve indicated, since an NFA is also allowed to have more than one initial state.)

Finally, these differences affect how we determine what words are accepted (or recognized) by an automaton.

If it’s a DFA, we know that each word completely determines the final state of the automaton, and we say that the word is accepted if that state is an acceptor state.

If it’s an NFA, there might be several possible final states that could result from reading a given word; as long as at least one of them is an acceptor state, we say that the automaton accepts the word.

~~갓 아메리카~~

똑같은 입력에 대해 NFA 는 다양한 최종상태를 만들 수 있다고 한다. 그래서 그 중 하나라도 accept 되면, 처리 된 것으로 받아들인다고 함. 어디서 주워들은 NP hardness 와 비스무리한 개념인것 같다. 그림을 다시 보면

(http://www-igm.univ-mlv.fr)

검색하려는 패턴, 즉 desired state 나열하고 transition 를 그려가며 DFA 를 만든다. 이를 이용해 텍스트를 파싱하면서 final state 에 도달하는지 보면 된다.

구현은

public int kmpStringSearch(String docs, String pattern) {
  int i, j;
  int N = docs.length(), M = pattern.length();
  Int[][] dfa = createDFA(pattern);
  
  for (i = 0, j = 0; i < N && j < M; i++) {
    j = dfa[txt.charAt(i)][j];
  }
  
  if (j == M) return i - M 
  else N
}

재밌는 사실은 backup 이 더이상 필요 없기 때문에 입력을 stream 으로 받을 수도 있다.

public int kmpStringSearch(In in, String pattern) {
  int i, j;
  int M = pattern.length();
  Int[][] dfa = createDFA(pattern);
  
  for (i = 0, j = 0; !in.isEmpty() && j < M; i++) {
    j = dfa[in.readChar()][j];
  }
  
  if (j == M) return i - M 
  else N
}

따라서 running time 은 DFA 만 있다면 확실히 N 번의 char access 다. 그럼 이제 문제는, DFA 를 만드는데 얼마나 시간이 걸릴것 인가?

DFA 를 만들면서 알아보자. ABABAC 의 패턴이 있을때

(1) match transition

현재 상태가 j 이고 다음 문자인 c 가 c == pattern.charAt(j) 이면 match transition 이므로 j++ 이다.

따라서 패턴 ABABAC 의 DFA 는

               j     0 1 2 3 4 5 
pattern.charAt(j)    A B A B A C

dfa[][j]          A  1   3   5
                  B    2   4  
                  C            6

(2) mismatch transition

상태 j 에서 c != pattern.chatAt(j) 이면, mismatch 다. 그러면 방금 전까지 만든 j-1 까지의 DFA 를 이용해서 pattern[1 .. j-1] 까지를 인풋으로 넣어 돌리면 된다. 무슨말인고 하니

ABABAC 에서 현재 state 가 5 면, 다음 인풋으로 C 를 받아야한다. ABABA^C 이렇게 표기하자. 그러면, ABABA 까지의 DFA 를 만들었으므로, 첫 문자 A 를 버리고 다음 문자 C 를 포함해서 BABAC 를 인풋으로 해서 DFA 를 돌리면 된다.

예를 들어 j = 5, c = A, B 에 대해 j = 4 까지의 DFA 를 짓고

               j     0 1 2 3 4 5 
pattern.charAt(j)    A B A B A C

dfa[][j]          A  1 1 3 1 5
                  B  0 2 0 4 0
                  C  0 0 0 0 0 6

에 대해서 BABA 를 반복하면, j = 3 이다. 따라서

dfa['A'][5] = dfa['A'][3] = 1
dfa['B'][5] = dfa['B'][3] = 4

이게 잘 보면 매번 j - 1 의 스텝을 반복해야하는 걸로 보일 수 있는데, 그러지 말고 pattern[1 .. j-1] 을 state X 라 부르고, 이걸 유지하면 transition 을 constant time 으로 지을 수 있다. 즉 j 가 하나 증가할 때 마다

X = dfa[pattern.charAt(j)][X]

이렇게 X 를 업데이트하면, j - 1 까지의 상태가 X 다. 따라서 DFA 를 linear time 으로 만들 수 있다.

Performance

DFA 를 만드는 속도는 M char access 이므로 전체 문서를 검색하는데 걸리는 시간은 M + N char access 다. (M 은 패턴의 길이, N 은 문서의 길이)

그러나 DFA 를 만드는데 필요한 메모리가 R * M 이다.

NFA 를 이용하면 KMP 알고리즘을 더 개선할 수 있다. M 에 비례하는 시간, 공간만으로도 패턴을 문서에서 탐색할 수 있다고 한다. KMPplus.java

KMP Implementation

구현하면

public class DFA {
	
	int[][] dfa;
	
	public DFA(String pattern, int R) {
		int M = pattern.length();
	
		// initialize
		dfa = new int[R][];
		for (int r = 0; r < R; r++)
			dfa[r] = new int[M];
		
		dfa[pattern.charAt(0)][0] = 1;
		
		// build DFA
		for (int X = 0, j = 1; j < M; j++) {
			// mismatch
			for (int c = 0; c < R; c++)
				dfa[c][j] = dfa[c][X];
			
			// match
			dfa[pattern.charAt(j)][j] = j + 1;
			
			// update X
			X = dfa[pattern.charAt(j)][X];
		}
	}

	public int search(String docs) {
		
		int i, j, M = pattern.length(), N = docs.length();
		
		for (i = 0, j = 0; i < N && j < M; i++) {
			j = dfa[docs.charAt(i)][j];
		}
		
		if (j == M) return i - M;
		else return N;
	}
}

Boyer-Moore

KMP 알고리즘은 linear time 인데, 이보다 더 빠르게 할 수 있을까?

(http://www.programering.com)

패턴의 우측부터 매칭해 가면, 꽤나 많은 M 사이즈의 텍스트를 빠르게 제낄 수 있다. 문제는 패턴이 어디까지 매칭되었는지에 따라 스킵할 수 있는 문자가 다르다는 것이다. 경우를 좀 나눠서 살펴보자 i 는 현재 문서의 탐색할 인덱스를, ^ 는 mismatch 를 나타낸다.

// case 1

          i     ^
. . . . . . . . T L E . . . . 
          N E E D L E
          
                  i
. . . . . . . . T L E . . . . 
                  N E E D L E

case 1 은 운이 좋아서, 미스매치 T 가 패턴에 없기 때문에 T 다음으로 i 를 옮길 수 있다.

// case 2a

          i     ^
. . . . . . . . N L E . . . . 
          N E E D L E
          
                i 
. . . . . . . . N L E . . . . 
                N E E D L E

여기선 mismatch 문자 N 이 패턴에 있기 때문에 rightmost N 을 찾아 다시 비교를 시작한다. (우측부터 비교하기 때문)

// case 2b

          i     ^
. . . . . . . . E L E . . . . 
          N E E D L E
          
// rightmost 'E'          

      i          
. . . . . . . . E L E . . . . 
      N E E D L E


// just increament `i` by 1

                i         
. . . . . . . . E L E . . . . 
            N E E D L E

이 경우엔 rightmost E 가 별로 도움이 안되므로, 그냥 i 를 증가시킨다.

다시 한번 정리하면,

(1) 우측부터 시작해서 비교하다 mismatch 문자가 있을 때 필요 없는 문자를 몇개나 제낄 수 있느냐 하는 문제는, 패턴 안에서 해당 mismatch 문자가 있느냐 없느냐에 따라 다르다.

(2) 없다면 모두 제껴버리면 되는거고,

(3) 있다면 그 문자가 얼마나 우측에 오느냐에 따라 스킵할 수 있는 문자의 수가 달라진다. 우측에 오면 올 수록 거기서 부터 다시 비교해야 하기 때문에, heuristic 이 별로 도움이 안될 수도 있다. case 2b 가 바로 그 예다. 그럴때는 그냥 1 만큼 증가시키는것이 더 나을 수도 있다.

skip table 을 만들면

int M = pattern.length();
int[] right = new int[R];

for (i = 0; i < R; i++) right[i] = -1;
for (j = 0; j < M; j++) right[pattern.charAt(j)] = j;

이 테이블을 이용해 탐색을 하면

int N = docs.length();
int M = pattern.length();

for (int i = 0; i <= N - M; i++) {
  int skip = 0;
  
  for (int j = M - 1; j >=0; j--) {
    if (docs.charAt(i + j) != pattern.charAt(j)) {
      skip = Math.max(1, j - right[docs.charAt(i + j)]);
      break;
    }
  }
  
  if (skip == 0) return i;
}

return N;

이 알고리즘에서 skip 을 계산하는 부분을 잘 보면

skip = Math.max(1, j - right[docs.charAt(i + j)]);

현재 비교가 진행된 j 에서 mismatch 문자의 인덱스를 뺄셈해서 1 보다 큰지를 비교한다. 만약 1 보다 작다면, 다시 말해 0 이나 음수라면 skip 이 마이너스로, 즉 왼쪽으로 되기 때문에 스킵할 필요가 없다. 그냥 우측으로 +1 해서 다시 비교하면 된다.

전체 코드는

public class BoyerMoore {
	
	int[] right;
	String pattern;

	public BoyerMoore(String pattern, int R) {

		this.pattern = pattern;
		int M = pattern.length();
	
		// initialize skip table
		right = new int[R];
		for (int i = 0; i < R; i++) right[i] = -1;
		for (int j = 0; j < M; j++) right[pattern.charAt(j)] = j;
	}
	
	public int search(String docs) {

		int M = pattern.length();
		int N = docs.length();
		
		for (int i = 0; i <= N - M; i++) {
			int skip = 0;
			
			for (int j = M - 1; j >=0; j--) {
				if (pattern.charAt(j) != docs.charAt(i + j)) {
					// calculate skip value
					skip = Math.max(1, j - right[docs.charAt(i + j)]);
					break;
				}
			}
			
			if (skip == 0) return i;
		}
		
		return N;
	}
}

이건 bad character 라는 특성을 이용한 방법이고, good suffix 등을 과 비교하여 얼마나 더 스킵할지를 결정할 수 있다.

보이어 무어 알고리즘에 대한 설명은 여기가 제일 잘 되어있다.

Performance

일반적으로는(휴리스틱) ~N/M 의 char compare 비교를 한다고 알려져있다. sublinear 한건데,

worst case 에서는 ~ MN 이다. 예를 들어 패턴이 ABBBB 고 문서가 BBBBBBBBBBBBBBBBB.. 일때 최악이다.

worst case 를 ~3N 까지 개선할 수 있다. KMP-like rule 을 더해 반복적인 패턴을 비하면 된다.

실제로 보이어 무어 알고리즘은 검색할 문자열이 길때 효과가 있다. 그래야 스킵할것이 많기 때문이다. 그러나 대부분의 경우 검색어가 그다지 길지 않다는 것.

Rabin-Karp

(http://terpconnect.umd.edu)

기본 아이디어는 modular hashing 이다. 인덱스를 하나씩 증가시켜가면서 문자열의 해싱 값을 비교한다.

먼저 해야할 일은 hash function 을 만드는 건데, t_i 를 문서(txt) 의 i 번째 캐릭터라 하면

$x_t = t_i R^{M-1}\ +\ t_{i+1} R^{M-2}\ +\ \cdots \ \ +\ t_{i+M-1} R^{0}\ \ (mod)\ \ Q$

여기서 M-digit, R-base, Q modulo 다. M-degree 다항식인데, Horner’s method 를 쓰면 중복된 계산 없이 linear time 으로 evaluation 가능하다.

(http://www.programering.com/)

난 첨에 뭔소린가 했는데 다항식의 값을 구할 때 중복된 계산을 피하기 위해 이렇게 구현하는걸 말한다.

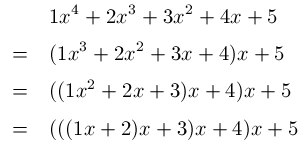
R 에 대한 다항식이기 때문에, 해싱함수의 구현은

private long hash(String key, int M, int Q) {
  long h = 0;
  
  for(int j = 0; j < M; j++)
    h = (R * h + key.charAt(j)) % Q;
    
  return h;
}

x_i 의 해싱값을 계산하고, 매칭이 안되면 다음으로 넘어가 x_(i+1) 을 계산해야 한다. 그런데, 좀 더 효율적으로 할 수 있는 방법이 없을까? 당연히 가능하다. 두 해싱값 서로 다른 1개의 항 빼고는 모두 같은 항을 가지고 있기 때문이다.

$x_i\ =\ t_iR^{M-1}\ +\ t_{i+1}R^{M-2}\ +\ \cdots\ +\ t_{i + M - 1}R^0\\ \ \\ \ \\ \ \\ \ \\ \ \\ x_i\ =\ t_{i + 1}R^{M-1}\ +\ t_{i+1}R^{M-2}\ +\ \cdots\ +\ t_{i + M}R^0$

따라서 x_(i+1) 은

$x_{i+1}\ =\ (x_i\ \ - t_iR^{M-1})\ *\ R\ +\ t_{i+M}$

이므로, 상수 시간 내에 다음 문자열의 해시값을 구할 수 있다. 따라서 매 i 마다 상수 시간이므로 ~N 으로 패턴을 찾을 수 있다.

(http://www.programering.com/)

Implementation

전체 코드는 RabinKarp.java 로

public class RabinKarp {
	
	String pattern;
	long patternHash;
	int M;
	long Q;
	int R;
	long RM; // R^(M-1) % Q

	public RabinKarp(String pattern) {
		this.pattern = pattern;
		
		R = 25;
		M = pattern.length();
		Q = longRandomPrime();
		
		// pre-compute R^(M-1) % Q for use in removing leading digit
		RM = 1;
		for (int i = 1; i <= M-1; i++)
			RM = (RM * R) % Q;
		
		patternHash = hash(pattern, M);
	}
	
	private long hash(String key, int M) {
		long h = 0;
		
		for (int j = 0; j < M; j++)
			h = (R * h + key.charAt(j)) % Q; 
		return h;
	}
	
	private static long longRandomPrime() {
		BigInteger prime = BigInteger.probablePrime(31, new Random());
		return prime.longValue();
	}
	
	public int search(String docs) {
		int N = docs.length();
		long docsHash = hash(docs, M);
	
		if (docsHash == patternHash) return 0;
		
		for (int i = M; i < N; i++) {
			// remove leading digit
			docsHash = (docsHash + Q - RM * docs.charAt(i-M) % Q) % Q;
			// add trailing digit
			docsHash = (docsHash * R + docs.charAt(i)) % Q;
			
			// match
			if (patternHash == docsHash) return i - M + 1;
		}
		
		return N;
	}
}

참고로, 해시값을 비교하는 것에는 두 가지 버전이 있다.

(1) Monte Carlo version: return match if hash match
(2) Las Vegas version: check for substring match if hash match and continue search if false collision.

몬테 카를로는 확률적으로 여러번 구해서 맞는 값을 찾는거다. 근데 만약에 Q 가 MN^2 정도로 상당히 크다면, 충돌이 일어날 확률은 1/N 이다.

실제 돌려보면 Q 를 충분히 크게 고르되, 오버플로우가 안 일어나면 1/Q 의 적은 확률로 충돌이 일어난다.

따라서

(1) Monte Carlo version

Always runs in linear time
Extremely likely to return correct answer (but not always)

(2) Las Vegas version

Always returns correct answer
Extremely likely to run in linear time (but worst case is M N)

라스베가스 버전에서 worst case 는, 충돌이 매번 나고 매번 검사하는건데. 그럴 일은 거의 없다.

Pros and cons

rabin-karp 알고리즘은 앞서 보았던 KMP 나 boyed moore 에 비해 장점이 있는데

Extends to 2d patterns
Extends to finding multiple patterns

예를 들어서 다양한 패턴을 찾고싶다 하면, 그 패턴들의 심볼 테이블을 만들어 놓고 검색하면 된다.

단점으로는

Arithmetic ops slower than char compares
라스베가스 버전은 백업을 필요로 함
poor worst case guarantee

Summary

References

(1) Algorithms: Part 2 by Ro$bert Sedgewick
(2) http://introcs.cs.princeton.edu
(3) Difference between NFA and DFA
(4) Automaton
(5) Boyer Moore string matching algorithm
(6) 보이어 무어 알고리즘에 대한 고찰
(7) Rabin-Karp Algorithm