Algorithm: Maximum Flow (Ford-Fulkerson)

Min Cut

edge weighted 그래프에서 st-cut 이란 vertices 를 두개의 disjont sets 으로 나누는 것이다. 이때 s, t 는 각각 다른 집합 A, B 에 속해있다.

(http://en.wikipedia.org)

capacity 란 컷으로 나뉘어진 두 집합 A, B 를 기준으로 A 에서 B 로 가기 위한 모든 edge 의 weight 를 모두 합친 것이다. B 에서 A 로의 edge 는 세지 않는 다는 것에 주의하자.

mincut problem 은 min capacity 를 갖는 cut 을 찾는 문제다. 응용으로는

  • 실제 전쟁에서 보급로를 끊거나
  • 독재 정부에서 커뮤니케이션을 제한하거나

Max Flow

(http://kunuk.wordpress.com)

edge 에 weight 이외에도 flow 를 할당할 수 있다. 이 플로우는 몇 가지 성질을 만족하는데

  • capacity constraint: 0 <= edge's flow <= edge's capa
  • local equilibrium: inflow = outflow at every vertex except s and t

즉 한 에지에서 캐퍼시티는 항상 플로우보다 크거나 같고, s, t 를 제외한 모든 노드에서 inflow = outflow 다.

flow 의 value 는 t 에서의 inflow 다. 이때 s 를 가리키는 노드가 없고, t 가 가리키는 노드가 없다고 가정한다. 다시 말해 s 는 시작점, t 는 종료지점이다.

따라서 플로우를 어떻게 할당하냐에 따라 value 가 달라질 수 있다. 이 때 maximum flow 문제는 최대 값을 갖는 flow 를 찾는 문제다.

max flow 의 응용은

  • 운송량을 최대로 하는 보급로를 찾기

Summary

정리하면 weighted digraph 에서 source vertex s, target vertex t 에 대해

두 가지 문제를 정의할 수 있다.

  • min cut: Find a cut of minimum capacity
  • max flow: Find a flow of maximum value

사실 이 문제는 상당히 유사한데, dual 관계다. 하나를 풀면 다른 하나도 풀 수 있다.

Ford-Fulkerson Algorithm

기본적인 아이디어는 augmenting path 를 찾으면서 flow 값을 증가시키는 것이다.

  • forward edge (not full) 을 이용해서 flow 값을 증가시키고
  • backward edge (not empty) 를 이용해서 감소시킬 수 있다

backward edge 의 아이디어는 local equilibrium 이다. 진행할 수 없는 상황에서 backward edge 를 만들고, 거기서 flow 의 평형을 맞추는 값만큼 뺀 후 다시 진행한다.

더이상 augmenting path 를 찾을 수 없을 때 알고리즘이 종료된다. 이건 full forward edge 가 존재하거나 empty backword edge 가 만들어졌기 때문이다.

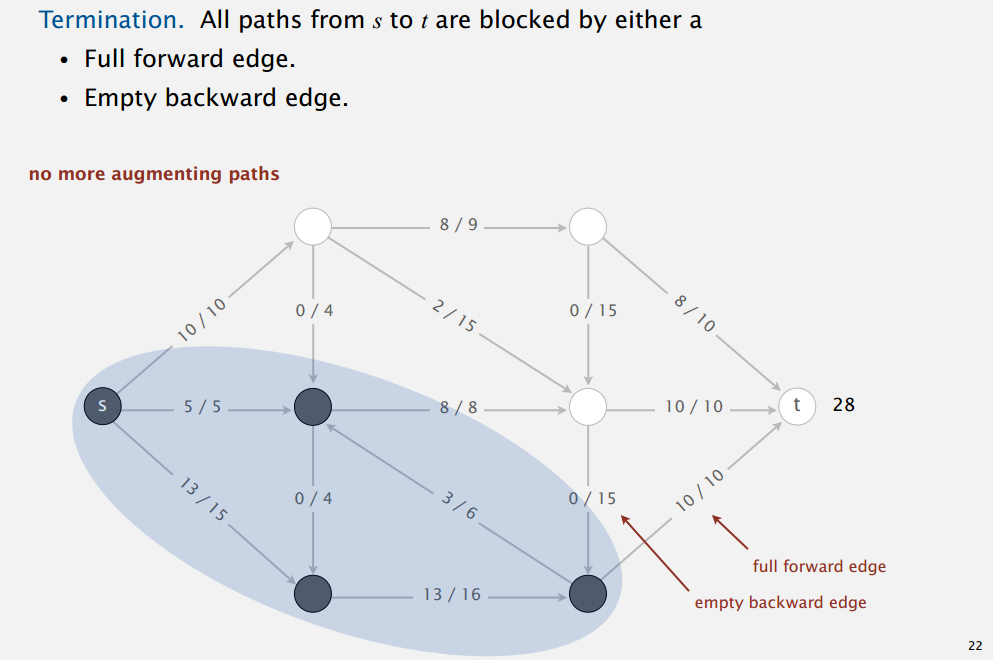
(http://www.cs.princeton.edu/)

알고리즘을 서술하면

// Fold-Fulkerson algorithm

Start with 0 flow
While there exists an augmenting path
- find an augmenting path
- compute bottleneck capacity
- increase flow on that path by bottleneck capacity

그럼, 이제 문제는 min cut 은 어떻게 계산하고 augmenting path 는 어떻게 찾을지로 치환된다.

그리고 추가적인 질문으로 FF 알고리즘이 max flow 를 찾는지, 그리고 항상 종료된다는 걸 보장하는지, 종료된다면 얼마만큼의 augmentations 를 찾아내는지를 물어볼 수 있다.

좀 더 자세한 알고리즘 설명은 이 슬라이드 를 참조할 것

Maxflow-Mincut Theorem

cut 과 flow 는 무슨 관계일까?

net flow accros cut (A, B) 는 A->B 로의 flow 를 모두 합한 것에서 B->A 로의 flow 를 모두 뺀 것이다.

flow-value lemma: Let f be any flow and let (A, B) be any cut. Then the net flow accros (A, B) equals the value of f

B 의 사이즈에 대해 귀납법을 이용하면 증명은 어렵지 않다.

(1) Base case B = { t }

base case 에선 당연히 value 와 net flow accros 가 동일하다.

(2) Inductive case

A 에서 B 로 vertex 를 하나씩 옮겨도 local equilibrium 이 참이므로 이 속성은 유지된다. 옮기려는 vertex 를 k 라 하면

k 를 기준으로 inflow

  • A -> k
  • B -> k

는 다음의 outflow 와 동일하다.

  • k -> A
  • k -> B

그런데 k 를 B 로 옮기게 되면 net flow accros 에 미치는 영향이 inflow, outflow 간 반대가 되지만 어쨌든 local equilibrium 에 의해 값은 같으므로 어차피 value 와 같다.

그리고 결국 k 를 계속 옮기다 보면s 의 outflow 는 t 의 inflow 와 같고 이것인 value of flow 와 같다.

Weak Duality

weak duality 란 f 를 아무 플로우, (A, B) 를 어느 컷이라 할 때

value of flow <= capacity of cut

이 성립함을 말한다. 따라서 max flow 는 min cut 이다. 증명과정을 좀 보자. 위에서 귀납법으로 참임을 보인 성질에 의해 다음이 성립한다. 뜬금없이 증명해버림

value of flow f = *net flow accros (A, B) <= capacity of (A, B)

  • Augmenting path theorem: A flow f is a maxflow iff no augmenting paths
  • Maxflow-mincut theorem: Value of the maxflow = capacity of mincut

즉 이 말은 동어 반복의 향연

(1) 플로우 f 의 value 와 동일한 값의 capacity 를 가지는 어떤 컷이 있다.
(2) f 는 max flow 다
(3) f 에 대해 augmenting path 가 없다.

정리해 보면 max flow 로 부터 min cut 을 계산할 수 있다는 소리가 된다. 잘 보면 max flow f 에서는 augmenting path 가 없다.

다시 말해

  • 한 집합은 s 에서 non-full forward 로 출발하지만 empty backward 에 의해 막히고
  • 다른 집단은 full foraward 때문에 t 로의 non empty backword 가 막힌다.
  • 이 두집단의 자르는 cut 은 full forward, empty backward 로만 구성된다.

이 컷은 net flow accros cut 고 첫번째 집단은 A, 두번째 집단은 B 가 된다.

따라서 러닝타임은 max flow f 가 주어진다면 모든 vertex, edge 를 한번씩 보며 A 를 찾는 시간이므로 V + E 다.

Running Time Analysis

(http://www.programering.com)

아까 했던 질문들에 답해보면

  • mincut 을 계산하긴 쉽다.
  • BFS 로 augmenting path 를 찾을 수 있다.
  • Ford-Fulkerson 이 종료되면 max flow 를 찾을 수 있다
  • capacity 가 정수거나, argumenting path 를 신중히 고른다면 FF 는 종료된다.
  • 얼마나 많은 augmentations 가 있을진 생각좀 해봐야 한다.

간단한 경우부터 좀 보자.

Integer Capacities

edge capacities 가 [1, U] 사이의 값이면 FF 알고리즘에 걸쳐서 모든 flow 값은 정수다. 쉽게 증명 가능한데

  • Bottleneck capacity is an integer
  • Flow on an edge increases / decreases by bottleneck capa

# of augmentations <= max flow value

다시 말해 augmentations 의 수는 max flow value 보다 작거나 같다. 왜냐하면 처음에 0 부터 시작해서 매 augmentation 마다 적어도 value 를 1 씩 증가시키기 때문이다.

  • Integrality theorem: There exists an integer-values maxflow

이 때 FF 알고리즘이 종료되면 max flow 를 찾아내고, 이것은 위에서 보였듯이 integer-value 를 가진다.

Bad case for FF

(http://www.programering.com)

integer value max flow 에선 운이 나쁠 경우 max flow value 만큼 augmentation 이 일어난다. 위 슬라이드에서 볼 수 있듯이 그래프 사이즈에 비해 어마어마한 augmentation 이 일어날 수 있다.

다행히도 shortest, fattest path 를 이용해 이런 상황을 피할 수 있다.

  • shortest path: augmenting path with fuwest number of edges
  • fattest path: augmenting path with maximum bottleneck capacity

(http://www.programering.com)

따라서 FF 알고리즘의 성능은 어떤 augmenting path 를 선택하느냐에 따라 달라질 수 있다.

Implementation

Ford-Fulkerson 알고리즘을 구현함에 있어서 실제로 사용하게 될 값은 두 가지다.

  • forward edge residual capacity = c - f
  • backward edge residual capacity = f

따라서 flow, capacity 보다는 residual capacity 를 edge 의 가중치로 표시하는 residual network 를 이용하는편이 더 직관적이다.

(http://www.programering.com)

실제 클래스 구현은

public class FlowEdge {
  
  private final int v, w;
  private final double capacity;
  private double flow;
  
  public FlowEdge(int v, int w, double capacity) {
    this.v = v; 
    this.w = w;
    this.capacity = capacity;
  }
  
  public int from() { return v; }
  public int to() { return w; }
  public double capacity() { return capacity; }
  public double flow() { return flow; }
  
  // other endpoint
  int other(int vertex) {
    if (vertex == v) return w;
    else if (vertex == w) return v;
    else throw new RuntimeException("Illegal endpoint");
  }
  
  // residual capacity toward v
  double residualCapacityTo(int vertex) {
    if (vertex == v)      return flow;            // backward edge
    else if (vertex == w) return capacity - flow; // forward edge
    else throw new IllegalArgumentException();
  }
  
  // add delta flow toward v
  void addResidualFlowTo(int vertex, double delta) {
    if (vertex == v)      flow -= delta; // backward edge
    else if (vertex == w) flow += delta; // forward edge
    else throw new IllegalArgumentException();
  } 
}

FlowNetwork 는

public class FlowNetwork {
  private final int V;
  // Bag is a list without remove op
  private Bag<FlowEdge>[] adj;
  
  public FlowNetwork(int V) {
    this.V = V;
    adj = (Bag<FlowEdge>[]) new Bag[V];
    for (int v = 0; v < V; v++)
      adj[v] = new Bag<FlowEdge>();
  }
  
  public void addEdge(FlowEdge e) {
    int v = e.from();
    int w = e.to();
    adj[v].add(e); // add forward edge
    adj[w].add(e); // add backward edge
  }
  
  public Iterable<FlowEdge> adj(int v) { 
    return adj[v];
  }

  public int V() { return V; }
}

FF 알고리즘 구현은 아래와 같다. shortest augmenting path 를 찾기 위해 BFS 를 이용했다.

public class FordFulkerson {

  private boolean[] marked;  // ture if s->v path in residual network
  private FlowEdge[] edgeTo; // last edge on s->v path
  private double value;      // value of flow
  
  public FordFulkersen(FlowNetwork G, int s, int t) {
    value = 0.0;
    
    while (hasAugmentingPath(G, s, t)) {
      double bottle = Double.POSITIVE_INFINITY;
      
      // compute bottleneck capacity
      for (int v = t; v != s; v = edgeTo[v].other(v))
        bottle = Math.min(bottle, edgeTo[v].residualCapacityTo(v));
      
      // augment flow
      for (int v = t; v != s; v = edgeTo[v].other(v))
        edgeTo[v].addResidualFlowTo(v, bottle);
      
      value += bottle;
    }
  }

  // find a shortest augmenting path using BFS
  private boolean hasAugmentingPath(FlowNetwork G, int s, int t) {
    edgeTo = new FlowEdge[G.V()];
    marked = new boolean[G.V()];
    
    Queue<Integer> q = new LinkedList<Integer>();
    q.add(s);
    marked[s] = true;
    
    while (!q.isEmpty()) {
      int v = q.remove();
      
      for (FlowEdge e : G.adj(v)) {
        int w = e.other(v);
        
        // path s->w is in the residual network?
        if (e.residualCapacityTo(w) > 0 && !marked[w]) {
          edgeTo[w] = e;
          marked[w] = true;
          q.add(w);
        }
      }
    }
    
    return marked[t];
  }
  
  public double value() { return value; }
  // is `v` reachable from s in residual network?
  public boolean inCut(int v) { return marked[v]; } 
}

(http://en.wikipedia.org)

테스트 코드도 좀 돌려보자. 예제는 위와 같고, 코드는 아래에 있다.

public class FordFulkensonTest {

  @Test
  public void test() {
    int E = 5;
    
    int s = 0;
    int t = 3;
   
    // http://en.wikipedia.org/wiki/Max-flow_min-cut_theorem#Example
    FlowEdge[] edges = new FlowEdge[E];
    edges[0] = new FlowEdge(s, 1, 4.0);
    edges[1] = new FlowEdge(s, 2, 3.0);
    edges[2] = new FlowEdge(1, 2, 3.0);
    edges[3] = new FlowEdge(1, t, 4.0);
    edges[4] = new FlowEdge(2, t, 5.0);
   
    int V = 4;
    FlowNetwork G = new FlowNetwork(V);
    
    for (FlowEdge e : edges)
      G.addEdge(e);
     
    FordFulkerson FF = new FordFulkerson(G, s, t);
    
    assert(FF.value() == 7);
  }
}

Max Flow Application

shortest path 처럼 max flow 도 정말 많은 곳에 응용할 수 있다.

  • Bipartite maching
  • Network reliability
  • Baseball elimination
  • Image segmentation
  • Distributed computing
  • …

Bipartite maching problem

(http://www.programering.com)

N 명의 student 가 N 개의 company 로부터 각각 몇개씩의 주문을 받았을 때, 1:1 로 대응하는 그래프를 그릴 수 있느냐의 문제다.

max flow 알고리즘을 이용해 bipartite maching 문제를 풀 수 있다.

  • Create s, t, one vertex for each student, and one vertex for each company(job)
  • Add edge from s to each student (capacity 1)
  • Add edge from each job to t (capacity 1)
  • Add edge from student to each job offered (infinite capacity)

이렇게하면 local equilibrium 에 의해 각 student 마다 하나씩의 out-flow 밖에 가지지 못하고, 마찬가지로 job 도 하나씩의 in-flow 밖에 가지지 못하므로 1:1 대응을 만들 수 있다.

완벽히 매칭이 이루어지는지, 아닌지를 min cut 을 이용해 알 수 있다. 그림을 보자.

(http://www.programering.com)

  • Let S = students on s side of cut.
  • Let T = companies on s side of cut.
  • |S| > |T|; students in S can be matched only to companies in T.

Baseball elimination

(http://www.programering.com)

Which teams have a chance of finishing the season with the most wins?

이건 게임이 얼마나 남았느냐 뿐만 아니라, 누구와 상대하냐도 문제가 되기 때문에 이렇게 그래프를 그려 풀 수 있다.

(http://www.programering.com)

여기서 디트로이트 (4) 는 수학적으로 봤을때 우승이 불가능하므로 미리 제거했다. 그리고, s 에서 출발하는 edge 를 각 팀간 남은 경기로, 그리고 t 로 들어가는 edge 를 디트로이트의 남은경기, 이긴경기에서 해당 팀의 이긴경기를 빼서 upper bound 를 설정한다.

Team 4 (디트로이트) not eliminated iff all edges pointing from s are full in max flow

Performance

max flow 문제의 경우 FF 알고리즘을 이용하면 worst case 에서 E^2U 성능이 나온다고 한다. 근데 이건 1955년도에 발견된 알고리즘이고, 가장 최근에는 compact network 라는 기법이 2012년에 만들어졌다. 이건 E^2 / log E 의 worst case performance 라고 함.

References

(1) Algorithms: Part 2 by Ro$bert Sedgewick
(2) http://introcs.cs.princeton.edu
(3) https://graph-tool.skewed.de/
(4) Wikipedia: Cut
(5) http://kunuk.wordpress.com - Flow
(6) http://www.programering.com
(7) Wikipeda - Max Flow



comments powered by Disqus