Algorithm Algorithm: R-way, Ternary Tries

Algorithm: R-way, Ternary Tries

String Symbol Table

지난 시간에 symbol-table 의 구현으로 red-black tree, hash table 의 성능을 살펴봤었다.

red black tree 는 search, insertion, delete 에 compareTo 를 이용해 log N, hash table 은 equals, hashCode 를 이용해 1 (under uniform hashing assumption) 의 성능을 확인했다.

red black tree 의 경우에는 rank 같은 다른 연산도 하는것도 봤다. 그런데, 이보다 더 빠르게 만들 순 없을까?

가능하다. 스트링 정렬처럼, entire key 를 모두 검사하지 않으면 더 빠르게 만들 수 있다. 먼저 시작 전에 String symbol table API 를 좀 보고가면

public class StringST<Value> {
  ...
  
  void put(String key, Value value)
  Value get(String key)
  void delete(String key)

  ...
}

Tries

red black tree 나 hash table 과는 다르게 한 노드에 key 가 아니라 character 를 저장한다. 아래 짤방을 보는게 이해가 더 빠를듯. 끝 초록색 노드에 붙어있는 숫자가 바로 value 다.

(http://t2.hhg.to)

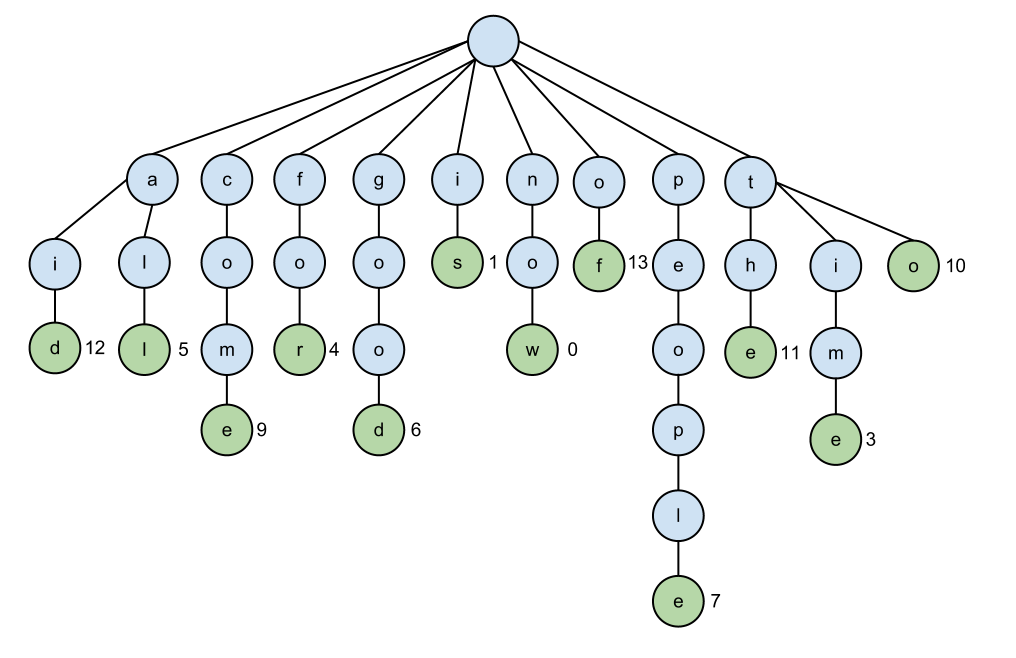
이름은 retrieval 에서 왔다고 한다. try 랑 똑같이 발음함. 허프만 코드랑 비슷하게도 보인다.

For now, store char in nodes (not keys)
Each node has R children, one or each possible chars
Store values in nodes corresponding to last chars in keys

value 는 항상 끝에만 있을 수 있는건 아니고 shell, she 둘 다 저장했을때 e 에도 she 를 위한 value 를 저장할 수 있다.

Trie Performance

Search hit

L 개의 문자를 모두 탐색해야 한다. 그리 긴 시간은 아님.

Search miss

첫 번째 문자부터 탐색에 실패할 확률도 있다. 전형적인 경우는 몇 개의 문자를 탐색하다 실패하는 경우이므로 sublinear 한 퍼포먼스를 보여준다.

각 leaf 마다 R 개의 널 링크가 필요한데, 그래도 sublinear 라고 말할 수 있는 것이 짧은 문자열들은 common prefix 를 공유한다.

Fast search hit and evn faster search miss, but waste spaces.

search miss 의 성능이 log_R N 으로 빨라져서 좋긴 한데, space 가 (R + 1) * N 이라 좀 부담이다. (search hit, insert 는 해시 테이블처럼 L)

유니코드면 65536-way trie 를 만들어야 한다.

유명한 job interview 로 efficient spell checking 의 자료구조를 구현하는 것이 있는데. 26-way tries 를 만들면 된다. value 는 bit 로

Deletion in an R-way Trie

만약 마지막 노드가 all null links 를 가지고 있으면 제거하면 된다. 그리고 백트래킹 하면서 value 를 만나기 전 까지 삭제되면 됨.

R-way Tries Implementation

public class TrieST<Value> {

	private static final int R = 256; // extended ASCII
	private Node root = new Node();
	private int N;

	private static class Node {
		private Object val;
		private Node[] next = new Node[R];
	}
	
	public TrieST() { N = 0; }
	
	public int size() { return N; }
	
	public boolean isEmpty() { return size() == 0; }

	public Value get(String key) {
		Node x = get(root, key, 0);
		
		if (x == null) return null;
		return (Value) x.val;
	}
	
	public void delete(String key) {
		root = delete(root, key, 0);
	}

	private Node delete(Node x, String key, int d) {
		if (x == null) return null;
		
		if (d == key.length()) {
			if (x.val != null) N--;
			x.val = null;
		} else {
			char c = key.charAt(d);
			x.next[c] = delete(x.next[c], key, d + 1);
		}
		
		// remove subtrie rooted at x if it is completely empty
		if (x.val != null) return x;
		for (int c = 0; c < R; c++)
			if (x.next[c] != null) return x;
		
		return null;
	}

	private Node get(Node x, String key, int d) {
		if (x == null) return null;
		if (d == key.length()) return x;
		char c = key.charAt(d);
		return get(x.next[c], key, d + 1);
	}
	
	public boolean contains(String key) {
		return get(key) != null;
	}

	public void put(String key, Value val) {
		if (val == null) delete(key);
		else root = put(root, key, val, 0);
	}

	private Node put(Node x, String key, Value val, int d) {
		if (x == null) x = new Node();
		if (d == key.length()) {
			if (x.val == null) N++;
			x.val = val;
			return x;
		}
		
		char c = key.charAt(d);
		x.next[c] = put(x.next[c], key, val, d + 1);
		return x;
	}
}

Ternary Search Tries

이전의 R-way 는 R 개의 자식들을 가졌지만, ternary 에서는 3 개만 가진다. ~~이것도 교수님이 만듬~~

Store chars and values in nodes (not keys)
Each node has 3 children; smaller, equal, larger

binary search 와 거의 유사하다. 그냥 key 를 string 로 사용하고 효율적인 검색을 위해 노드에 character 를 저장한다는 점만 다르고. 이 차이점을 그냥 교수님은 tree 가 아니라 trie 라 부르는 것 같다.

어쨌든 ternary 는 r-way 보다 null link 자체가 훨씬 적다. 따라서 메모리 사용량에 부담 없고, hash table 보다 상당히 빠른 search miss 를 보여준다. 구현은 여기로

TST Impelementation

public class TernaryST<Value> {

	private int N;
	private Node root;
	
	private class Node {
		private char c;
		private Value val;
		private Node left, mid, right;
	}
	
	public TernaryST() { N = 0; }
	
	public int size() { return N; }
	public boolean isEmpty() { return size() == 0; }
	
	public boolean contains(String key) {
		return get(key) != null;
	}
	
	public Value get(String key) {
		if (key == null) throw new NullPointerException();
		if (key.length() == 0) throw new IllegalArgumentException("key shouldn't be empty");
		
		Node x = get(root, key, 0);
		if (x == null) return null;
		return x.val;
	}

	private Node get(Node x, String key, int d) {
		if (key == null) throw new NullPointerException();
		if (key.length() == 0) throw new IllegalArgumentException("key shouldn't be empty");
		if (x == null) return null;
		
		char c = key.charAt(d);
		if      (c < x.c) 				return get(x.left, key, d);
		else if (c > x.c) 				return get(x.right, key, d);
		else if (d < key.length() - 1)  return get(x.mid, key, d + 1);
		else 							return x;
	}
	
	public void put(String key, Value val) {
		if (!contains(key)) N++;
		root = put(root, key, val, 0);
	}

	private Node put(Node x, String key, Value val, int d) {
		char c = key.charAt(d);
		
		if (x == null) {
			x = new Node();
			x.c = c;
		}
		
		if 		(c < x.c) 				x.left = put(x.left, key, val, d);
		else if	(c > x.c) 				x.right = put(x.right, key, val, d);
		else if (d < key.length() - 1)	x.mid = put(x.mid, key, val, d + 1);
		else 							x.val = val;
				
		return x;
	}	
}

항상 느끼는건데, imperative 언어에서의 재귀가 더 어려운 것 같다.

TST Performance

(1) R-way trie

search hit: L
search miss: log_R N
insert: L
space: (R + 1) * N

(2) Ternary trie(TST)

search hit: L + ln N
search miss: ln N
insert: L + ln N
space: 4N

메모리가 4N 밖에 안든다! 해싱은 모든 연산이 L 이겠지만, 대신 메모리가 4N ~ 16N 이다.

따라서 ternary symbol table 은 hash table 만큼 빠르고, 메모리도 덜 든다.

참고로 rotation 연산을 이용해서 balanced TST 를 만들면 worst case 에도 L + logN 이 나온다.

TST with R2 Branching at root

꼭대기엔 R^2-way 로 짓고, 자식은 TST 로 지을 수 있다. 분석 결과로는 일반 TST 보다 더 빠르다고 한다.

TST vs Hashing

(1) Hashing

Need to examine entier key
Search hits and misses cost about the same
Performance relies on hash function
Does not support ordered symbol table operations.

(2) TST

Works only for strings (or digital keys)
Only examines just enough key characters
Search miss may involve only a few characters
Supports ordered symbol table operations (plus others!).

정리하면, TST 는 해싱만큼 빠르고 search miss 는 더 빠르다. 그리고 red-black BST 보다 유연하다. 그러나 자료의 형태에 제한이 있다.

Character-Based Operations

string symbol table 의 경우에는 유용한 chars-based operation 을 제공한다.

prefix match
wildcard match
longest prefix

API 를 보면

public class SymbolST<Value> {

  ...
  ...
  
  Iterable<String> keys()
  Iterable<String> keysWithPrefix  (String s)
  Iterable<String> keysThatMatch   (String s)
  String           longestPrefixOf (String s) 
  
  ...
  ...
}

이 외에도 ordered ST 를 위한 floor, rank 등의 연산도 추가할 수 있다.

Inorder Traverse of Trie

탐색이 이진트리하고 좀 다른게, 매 문자열마다 시작점부터 시작해야 된다. leaf 까지 방문하는건 같은데

(http://en.wikipedia.org/wiki/Trie)

public Iterable<String> keys() {
  Queue<String> q = new Queue<String>();
  collect(root, "", q);
  return q;
}

public void collect(Node x, String prefix, Queue<String> q) {
  if (x == null) return;
  if (x.val != null) q.enequeue(prefix);
  
  for (char c = 0; c < R; c++)
    collect(x.next[c], prefix + c, q);
}

queue 는 단순히 she 를 방문할때 she 를 저장하기 위한 용도다. val != null 일 때 저장하므로 s, sh 등은 저장하지 않는 다는 점에 유의하자.

그리고 여기서 큐는 DFS, BFS 처럼 로직에 쓰이지 않는다. 모든 노드를 방문하긴 하는데 c = 0 부터 시작하니 왼쪽부터 방문하는 재귀 순회라 보면 쉽다.

여기서 collect 함수는 인자로 받은 노드 x 를 기준으로 하위에 있는 substring 을 찾아낸다.

실제 구현에서는 StringBuilder 를 사용한다.

	private void collect(Node x, StringBuilder prefix, Queue<String> q) {
		// TODO Auto-generated method stub
	
		if (x == null) return;
		if (x.val != null) q.add(prefix.toString());
		
		for (char c = 0; c < R; c++) {
			prefix.append(c);
			collect(x.next[c], prefix, q);
			prefix.deleteCharAt(prefix.length() - 1);
		}
	}
	
	public Iterable<String> keys() { return keysWithPrefix(""); }

Prefix Matchs

구글링 하면서 매일 사용하는 기능이다. 구현은 위의 collect 함수를 사용하면 쉽다. keyWithPrefix("sh") 라면, sh 까지 내려간 뒤 collect 를 호출하면 된다.

public Iterable<String> keysWithPrefix(String prefix) {
  Queue<String> q = new Queue<String>();
  Node x = get(root, prefix, 0);
  collect(x, prefix, q);
  return q;
}

자바의 Queue 는 인터페이스이므로 실제 구현은

	public Iterable<String> keysWithPrefix(String prefix) {
		Queue<String> q = new LinkedList<String>();
		Node x = get(root, prefix, 0);
		collect(x, new StringBuilder(prefix), q);
		return q;
	}

Longest Prefix

라우터에서 자주 사용한다. 아이피를 문자열로 표현하고, 자기가 알고 있는 인접한 라우터중 어디로 보낼지를 결정하기 위해 longest prefix 를 알아내 보낸다.

longestPrefixOf("128.112.136.11") 
// 128.112.136

아이디어는 간단하다. null 이나 찾으려는 문자열의 마지막 문자를 만나기 전까지의 문자열을 모아 돌려주면 된다.

public String longestPrefixOf(String query) {
  int length = search(root, query, 0, 0);
  return query.substring(0, length);
}

public int search(Node x, String query, int d, int length) {

  if (x == null) return length;
  if (x.val != null) length =  d;
  if (d == query.length) return length;
  
  char c = query.charAt(d);
  return search(x.next[c], query, d + 1, length);
}