Functional Programming 6

지난 시간에는 referential transparency (참조투명성) 과 함수형 언어에서의 귀납법인 structural induction 에 대해서 배우고, 몇 개의 예제를 증명했었다.

이번 시간에는 스칼라의 컬렉션인 Seq, Set, Map 을 알아보고 마지막 챕터에서는 여기에 higher-order function 을 더해 미친듯한 표현력을 가진 코드를 작성해 본다. one-liner 의 절정을 보여주시는 교수님

(번역이 서툴러 어중간한 의역을 하느니 단어를 그대로 사용하고 필요할 경우 원문을 첨부한다)

Other Collections

Vector

List 는 처음 원소는 O(1) 로 빠르게 접근하지만, 중간이나 마지막 원소에 대해서는 조금 느린편이다. 만약에 중간이나 마지막 원소에 대한 탐색을 빠르게 하고싶다면 다른 sequence implementation 인 Vector 를 사용하면 된다. Vector 는 다른 원소들에 대한 접근이 evenly balanced 하다.

This one has more evenly balanced access pattern then List.

Vector 는 2^5 = 32 개의 원소를 가진 리스트의 트리로 구현된다. 따라서 처음 단계에서는 2^5 개를 저장할 수 있고, 그 다음 단계에서는 2^5 * 2^5 = 2^10, 그 다음 단계에서는 2^15 를 저장할 수 있다. 2^5 의 배수만큼 증가하는 것이다. binary tree 에서 자식의 갯수가 2 개가 아니라 32 개라고 생각하면 된다.

이런 이유로, 원소를 탐색하는데 걸리는 시간은 log_32 (N) (32 based-log) 라 보면 된다. random access 에 대해서는 List 보다 훨씬 낫다.

Vector 의 또 다른 장점은 map, for 같은 bulk operator 에 대해서 빠른 연산이 가능하다는 것이다. 이것은 원소들이 32개씩 뭉쳐있기 때문에 single cache line 에 있을 확률이 높아진다. 리스트의 경우에는 콘셀이 같은 cache line 에 있으리라는 보장이 없기 때문에 Vector 보다 locality 가 떨어진다.

그럼 List 가 필요없을까? 그렇지 않다. head, tail 과 같은 연산을 할때 빠르다. 깊이가 깊은 Vector 구조에서, head 나 tail 의 경우 몇 번의 연산이 필요한지 생각해보면 쉽게 이해할 수 있다.

(1) map, for 과 같은 bulk operation 은 Vector 가
(2) tail, head 는 List 가 더 빠르다.

Vector 는 대부분의 List 연산을 사용할 수 있는데 예외가 하나 있다. 바로 :: 콘싱은 List 를 위한 연산이기 때문이다.

따라서 Vector 에서는 원소 추가나, 패턴 매칭을 위해 x +: xs, x :+ x 를 사용하면 된다.

Vector 는 List 처럼 immutable 이기 때문에 원소를 추가하면 기존의 데이터는 변경되지 않는다. 따라서 가장 깊은 깊이에 새로운 Vector 를 추가하고 그 벡터를 가리키는 상위 벡터, …, 루트 벡터까지 만드는 비용은 log32(N) 이 된다. 물론 이건 object creation 비용이다.

Sequence

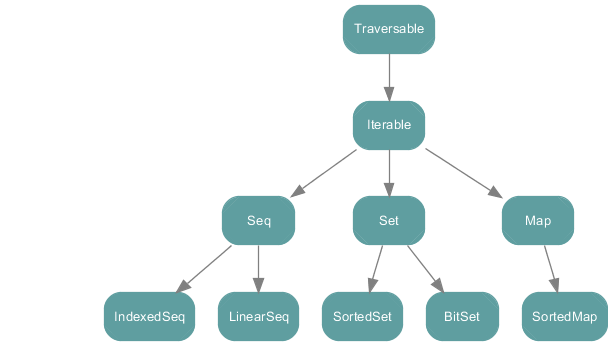
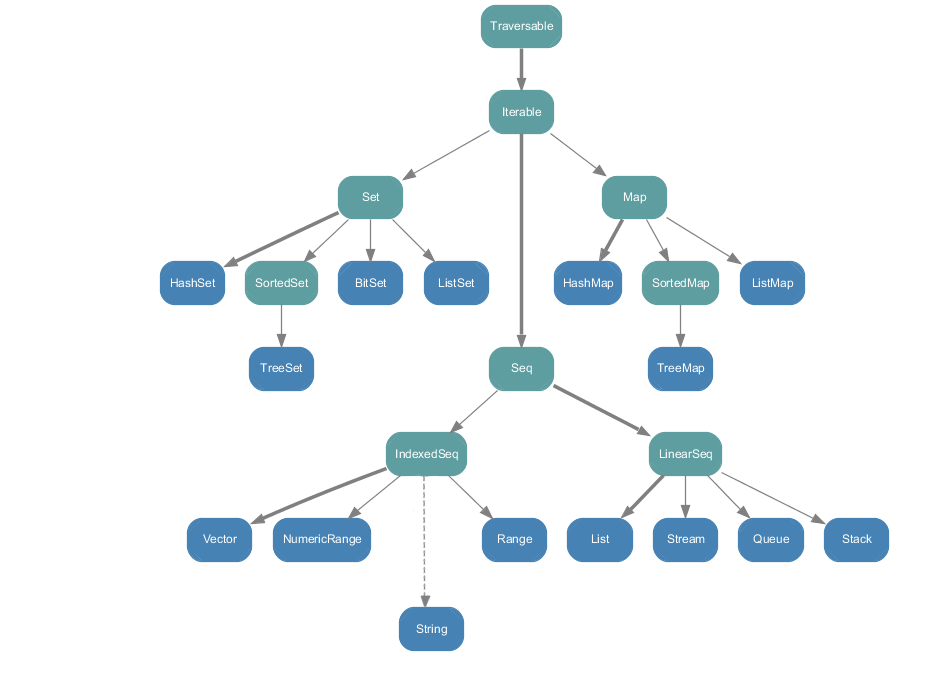
Vector, List, Range 는 Seq 의 sub-type 다. Seq 이외에도 Set, Map 등이 있으며 Seq, Set, Map 은 Iterable 의 sub-type 이다. hierarchy 를 살펴보면,

(http://docs.scala-lang.org)

(http://docs.scala-lang.org)

Array 와 String 은 점선으로 연결된 걸 볼 수 있는데 이건 두 클래스가 Java 에서 왔기 때문이다. 스칼라 클래스는 아니지만 스칼라의 Seq 로 볼 수 있다. (View) 따라서 다음과 같은 코드는 정상 동작한다.

"Hello World" filter { c => c.isUpper }

Range

다른 Seq 구현체로는 Range 가 있다. Range 는 evenly spaced intergers 를 나타낸다.

val r: Range = 1 until 5 // Range(1, 2, 3, 4)
val s: Range = 1 to 5 // Range(1, 2, 3, 4)
1 to 10 by 3
6 to 1 by -2

그렇기에 Range 는 upper bound, lower bound, step value 를 클래스의 멤버로 가지고 있다.

Sequence Operations

Seq 에 대해서 exists, forall, zip, unzip, flatMap, sum, product, max 등을 사용할 수 있다.

zip 은 두개의 Seq 의 각 원소를 pair 로 묶는거고, unzip 은 각 pair 를 푼다.

scala> a
res13: scala.collection.immutable.Range.Inclusive = Range(1, 2, 3, 4, 5)

scala> b
res14: List[Char] = List(h, e, l, l, o)

scala> a zip b
res15: scala.collection.immutable.IndexedSeq[(Int, Char)] = Vector((1,h), (2,e), (3,l), (4,l), (5,o))

scala> a zip b unzip
res16: (scala.collection.immutable.IndexedSeq[Int], scala.collection.immutable.IndexedSeq[Char]) = (Vector(1, 2, 3, 4, 5),Vector(h, e, l, l, o))

flatMap 은 각 원소에 map 을 적용한 ’¤, 풀어 헤친다. 예를 들어

scala> "HelloWorld" flatMap { c => List('.', c) }
res17: String = .H.e.l.l.o.W.o.r.l.d

flatMap 은 맵을 두번하면 할 때 자주 쓰인다. 예를 들어 n, m 에 대해 combinator (조합) 을 찾을때 flatMap 을 사용하면 Vector 의 Vector 가 아니라 Vector 만 얻는다.

1 to m flatMap { x => 1 to n map { y => (x, y) } }

벡터에 대해 스칼라 곱을 하고 싶다면, zip 을 이용할 수 있다. zip 을 이용하면 두 Seq 의 pair 가 나오므로, 곱한 후 sum 하자.

(xs zip ys).map(xy => xy._1 * xy._2).sum

그런데, zip 해서 나오는 pair 에 패턴매칭을 적용할 수 있으므로

(xs zip ys).map { case(x, y) => x * y }.sum

참고로, x => match { case ... } 은 { case ... } 으로 바로 줄여쓸 수 있다.

Combinatorial Search and For-Expression

Handling Nested Sequences

보다 작은 두 수 i, j (1 <= j < i < n) 에 대´서 i + j 가 소수인 i, j 를 찾는다고 하자.

Given a positive integer n, find all pairs of positive integers i and j with 1 <= j < i < n such that i + j is prime

이렇게 코드를 작성해 볼 수 있다.

1 until 5 flatMap { i => 1 until i map { j => (i, j) }}

res36: scala.collection.immutable.IndexedSeq[(Int, Int)] = Vector((2,1), (3,1), (3,2), (4,1), (4,2), (4,3))

재밌는 사실은 Range 를 사용했음에도 Vector 가 나온다는 점이다. 더 정확히는 IndexedSeq 다. 무슨 일이 일어난 걸까? Range 는 Pair 를 원소로 가질 수 없기 때문에 상위 타입인 IndexedSeq 를 가지게 되고, 이것의 구체적 타입인 Vector 가 된다.

(http://docs.scala-lang.org)

flatMap 을 안쓰면 Vector 의 Vector 가 나오는데, 여기에 foldRight Seq[Int]() (_ ++ _) 을 사용하거나 아니면 flatten 을 사용할 수도 있다.

(1 until 5 { i => 1 until i map { j => (i, j) }}).flatten

결국 flatMap 은 map 후 flatten 을 적용한 결과를 돌려줌을 알 수 있다. 이제 여기에 filter 를 적용하면 처음에 주어졌던 문제를 해결할 수 있다.

    1 until n flatMap { i => 1 until i map {j => (i, j)} } filter { case (i, j) => isPrime(i + j)}

For-Expression

map 과 같은 higher-order function 은 expressive 한데 읽기가 좀 힘들때가 있다. 스칼라에서는 이를 위해 for 을 제공한다. 다음의 두 문자을 보자. 완전히 동일하다.

case class Person(name: String, age: Int)

for (p <- persons if p.age > 20) yield p.name
persons filter (p => p.age > 20) map (p => p.name)

for 는 imperative language 의 그것과 비슷하긴 한데, 스칼라의 for 은 무언갈 변경하지 않고 새로운 List 를 yield 를 통해 생성한다.

for (s) yield e 문법을 좀 자세히 살펴보자.

where s is a sequence of generators and filters, and e is an expression whose value is returned by an iteration

generator 는 p <- e 형태의 form 인데 p 는 pattern 이고 e 는 value 로 collection 을 가진 expression 이다.

filter 는 Boolean expression 을 가지는 form 이다.

for 루프 여러개 중첩하는 것처럼 generator 가 여러개 일 수 있는데, 이 경우 마지막에 오는 generator 가 여러번 돈다.

If there are several generators in the sequence, the last generators vary faster than the first.

그리고 ( s ) 대신에 { s } 를 사용할 수도 있는데, 이러면 세미콜론 없이 filter 와 generator 를 여러줄에 걸쳐서 작성할 수 있다.

이제 처음에 나왔던 문제를 for 로 작성해 보자.

for {
  i <- 1 until n
  j <- 1 until i
  if isPrime(i + j)
} yield (i, j)

읽기„ 쉬워졌다. flatMap 따위

이제 아까 나왔던 벡터간 스칼라 곱을 하는 함수를 다시 작성해 보면

def scalaProduct(xs: List[Double], ys: List[Double] =
    (for ((x, y) <- xs zip ys) yield (x * y)).sum

해보면 알겠지만 for { x <- xs; y <- ys } yield x * y sum 은 안된다. 루프가 중첩되기 때문이다.

Combinatorial Search Example

자 이제 Seq 말고 Set 에 대해서 알아보자. Seq 의 대부분의 연산도 사용할 수 있고, 비슷비슷허다. Seq 와 Set 은 Iterable 의 sub-type 이므로 Iterable 스칼라독을 보면 어떤 연산을 사용할 수 있는지 확인 할 수 있다.

Seq 와의 차이점은 다음과 같다.

(1) Set 은 순서가 없다.
(2) Set 은 중복된 원소를 가질 수 없다.
(3) contain 이 fundamental operation 이다.

val a = 1 to 4 toSet

scala> a
res53: scala.collection.immutable.Set[Int] = Set(1, 2, 3, 4)

scala> a map (_ / 2)
res54: scala.collection.immutable.Set[Int] = Set(0, 1, 2)

N-Queens Problem

이제 Set 을 이용해 좀 문제를 풀어보자.

The n-queens problem is to place n queens on a chess board so that no queen is threatened by another

In other words, there can’t be two queens in the same row, column, or diagonal

모든 조합을 뽑아내고, 열을 List 로 표현하고, 그 순서를 행이라 한 뒤 모든 조합을 뽑아내 Set 에 넣으면 자동으로 중복된 결과가 제거된다. 로직은 다음과 같다.

(1) 내게 placeQueens 라는 1 개의 퀸을 위치시킬 수 있는 함수가 있다.
(2) n = 1, 2, ... , n 으로 placeQueens 를 재귀적으로 호출해 가며 이전 단계에서 얻은 퀸들을 이용하여 하나의 퀸을 새롭게 배치한다.
(3) 각 단계에서는 새 퀸을 배치할 수 있는지 없는지 검사할 isSafe 함수가 필요하다.

이게 Recursion 에서 문제를 풀 때 기본적으로 필요한 생각인 것 같다. 문제를 작게 잘라 매번 1/n 씩 해결할 수 있다면 이라 가정 한 뒤 1/n 문제를 풀기 위한 함수와 1/n 문제의 종료조건을 정의하는 것. 우리의 경우엔 그 함수가 isSafe 였다.

  def nQueens(n: Int): Set[List[Int]] = {

    def isSafe(col: Int, queens: List[Int]): Boolean = {
      val row = queens.length // where new queen will be placed
      val queensWithRow = (row - 1 to 0 by -1) zip queens
      queensWithRow forall {
        case (r, c) => col != c && math.abs(col - c) != row - r
      }
    }

    def placeQueens(k: Int): Set[List[Int]] =
      if (k == 0) Set(List())
      else
        for {
          queens <- placeQueens(k - 1)
          col <- 0 until n
          if isSafe(col, queens)
        } yield col :: queens

    placeQueens(n)
  }

diagonal 을 어떻게 검사할까가 고민이 될 수 있겠는데, 사실 생각해보면 쉽다. 컬럼의 차이와 행의 차이가 같으면 diagonal 인 것.

여기에 출력하기 위한 함수를 요로코롬 만들고 출력하면

  def showQueens(queens: List[Int]) = {
    val lines =
      for {
        col <- queens.reverse
      } yield Vector.fill(queens.length)("[ ]").updated(col, "[*]").mkString

    "\n\n" + (lines.mkString("\n"))
  }


[ ][ ][*][ ]
[*][ ][ ][ ]
[ ][ ][ ][*]
[ ][*][ ][ ],

[ ][*][ ][ ]
[ ][ ][ ][*]
[*][ ][ ][ ]
[ ][ ][*][ ]

nQueens(8) take 3 map show 처럼 응용도 가능하다.

Queries with For

지난 시간에 배운 for 는 SQL 과 비슷한데 좀 더 자세히 살펴보자. 다음과 같은 case class 가 있다고 하자.

case class Book(title: String, authors: List[String])

이제 다음과 같은 코드를 이용해 쿼리처럼 질의할 수 있다.

for {
  b <- books
  a <- b.authros
  if a startWith "Bird")
} yield b.title

for {
  b <- books
  if b.title indexOf "Programming" >= 0
} yield b.title

for {
  b1 <- books
  b2 <- books
  if b1 != b2
  a1 <- b1.authors
  a2 <- b2.authors
  if a1 == a2
} yield a1

세번째 for 문은 약간 문제가 있는데 내용이 똑같고 순서만 다른 List 를 만들 수 있다 따라서 중복을 피하기 위해 < 를 비교로 사용하자.

for {
  b1 <- books
  b2 <- books
  if b1.title < b2.title
  a1 <- b1.authors
  a2 <- b2.authors
  if a1 == a2
} yield a1

근데 만약에 같은 작가가 3개의 책을 출판했다면? title 이 a < b < c 와 같은 순서를 가지므로 (a, b), (a, c), (b, c) 처럼 비교되어 3번 출력된다.

중복을 제거하기 위해 distint 를 사용할 수 있다. 더 좋은 방법은 Set 을 사용하면 된다.

Translation of For

for 을 이용하면 map, flatMap, filter 를 쉽게 구현할 수 있는데

def mapFun[T, U](xs: List[T], f: T => U): List[U] =
  for (x <- xs) yield f(x)

def flatMap[T, U](xs: List[T], f: T => Iterable[U]): List[U] =
  for (x <- xs; y <- f(x)) yield y

def filter[T](xs: List[T], p: T => Boolean): List[T] =
  for (x <- xs; if (p(x)) yield x  

사실 스칼라 컴파일러는 for 을 map, flatMap, lazy variant of filter 로 바꿔치기한다.

Scala compiler expresses for expressions in terms of map, flatMap and a lazy variant of filter

예를 들어 for (x <- e1) yield e2 는 e1.map(x => e2) 로 바꾼다

for (x <- e1 if f; s) yield e2

f 가 filter 고 s 가 sequence of generators and filters 라면 다음과 같이 번역된다.

for (x <- e1.withFilter(x => f); s) yield e2

여기서 withFilter 는 바로 적용되는 것이 아니라, 뒤 따라오는 map 또는 flatMap 등에 적용된다고 보면 된다. 원문을 첨부하면

You can think of withFilter as a variant of filter that does not produce an intermediate list, but instead filters the following map or flatMap function application

for (x <- e1; y <- e2; s) yield e3

이건 다음처럼 번역된다.

e1.flatMap(x => for (y <- e2; s) yield e3)

그리고 내부의 for € 다시 한번 더 번역된다.

for {
  i <- 1 until n
  j <- 1 until i
  if isPrime(i + j)
} yield (i, j)

이것은

(1 until n) flatMap(i =>
  (1 until i).withFilter(j => isPrime(i + j))
  .map(j => (i, j)))

이제 아까 lazy variant of filter 어쩌구 하던 내용을 이해할 수 있는데, 중간에 withFilter 는 1 until i 에 적용 되는것이 아니라 map 이 만들어낸 pair (i, j) 에 대해 적용된다.

다시 말해 for 문에서 if guard 는 나중에 적용되는 withFilter 다.

for (b <- books; a <- b.authros if a startsWith "Bird") yield b.title

요건 이렇게 번역된다.

b.flatMap(b => b.authors.withFilter(a => a.startsWith "Bird").map(x => x.title)

for 는 다양한 컬렉션에도 적용할 수 있는데 이는 for 가 map, flatMap, withFilter 이 3개의 함수를 기반으로 만들어졌기 때문이다. 따라서 커스텀 타입에도 이 3개의 함수를 만들면 for 를 사©할 수 있다.

이런 이유로 데이터베이스 클라이언트가 map, flatMap, withFilter 같은 메소드를 정의하면 for 을 이용해 쿼리할 수 있다.

이것이 바로 ScalaQuery 나 Slick 같은 스칼라 데이터베이스 프레임워크가 사용하는 방법이다. LINQ 도 비슷한 개념이다.

Maps

자 이제 Seq, Set 을 살펴보았으니 Map 을 알아보자.

Map 은 Iterable 일뿐만 아니라 Function 이다. 그래서 함수 호출하듯이 Key 를 인자로 주어 호출하면 Value 를 얻을 수 있다. 그러나 없는 Key 에 대해서 호출하면 NoSuchElementException 이 발생한다.

예외 대신에 있는지 없는지 알려면 get 을 이용하면 된다. 없으면 None 있으면 Option[Value] 를 돌려준다.

Option Type

Option 은 Trait 인데

trait Option[+A]
case class Some[+A](value: A) extend Option[A]
object None extend Option[Nothing]

covaraint 기 때문에 Option[Type]  None 을 넣을 수 있다. None 은 Option[Nothing] 이므로 모든 Option 의 하위타입이다. 참고로 get 의 결과에 패턴매칭을 이용할 수 있다.

Sorted and GroupBy

SQL Query 처럼 sorted 와 groupBy 를 이용할 수 있다.

scala> fruit
res70: List[String] = List(apple, pear, orange, pineapple)

scala> fruit.sorted
res71: List[String] = List(apple, orange, pear, pineapple)

scala> fruit.sortWith(_.length < _.length)
res72: List[String] = List(pear, apple, orange, pineapple)

scala> fruit.groupBy(_.head)
res73: scala.collection.immutable.Map[Char,List[String]] = Map(p -> List(pear, pineapple), a -> List(apple), o -> List(orange))

groupBy 는 컬렉션을 discriminator 를 이용해 Map 으로 파티셔닝한다.

Ploynomials (다항식) 을 Map 을 이용해 표현해 보자. 다항식은 각 차수가 한개씩 있고, 상수도 하나씩 붙어 있으므로 Map 으로 표현하기에 적합하다.

  class Poly(val terms: Map[Int, Double]) {
    def + (other: Poly): Poly = new Poly(terms ++ other.terms)
    override def toString = {
      (for((exp, coeff) <- terms.toList.sorted.reverse) yield  coeff + "x^" + exp) mkString " + "
    }
  }

이렇게 만들면 제대로 된 계산이 안된다. 왜냐하면 Map 의 ++ 오른쪽에 오는 Map 에 똑같은 key 를 가지고 있는 원소가 있으면 덮어 쓰기 때문이다. 다항식에서 차수가 같으면 coefficient (계수) 를 덧셈해야 하는데 덮어씌우면 올바른 계산이 아니다. 따라서 other.terms 에 같은 Key 를 가진 원소가 있나 없나 계산해서 있으면 현재 terms 와 계수를 더한 새로운 pair 를 돌려줘야 한다. (Map 의 원소는 pair 다)

  class Poly(val terms: Map[Int, Double]) {
    def + (other: Poly): Poly =
    new Poly(terms ++ (other.terms map adjust))

    def adjust(term: (Int, Double)): (Int, Double) = {

      val (exp, coeff) = term

      terms.get(exp) match {
        case None => term
        case Some(coeff1) => (exp, coeff + coeff1)
      }
    }

    override def toString = {
      (for{
        (exp, coeff) <- terms.toList.sorted.reverse
      } yield  coeff + "x^" + exp) mkString " + "
    }
  }

Default Values

Map 은 partial function 이기 때문에 없는 Key 에 대해 Map 을 호출하면 예외가 발생한다.

Map 에 withDefaultValue 를 적용하면 total function 으로 바꿀 수 있다. Poly 에 적용해 보자.

  class Poly(val terms0: Map[Int, Double]) {
    val terms = terms0 withDefaultValue 0.0
    def + (other: Poly): Poly = new Poly(terms ++ (other.terms map adjust))
    def adjust(term: (Int, Double)): (Int, Double) = {

      val (exp, coeff) = term
      (exp, coeff + terms(exp))
    }
    override def toString = {
      (for{
        (exp, coeff) <- terms.toList.sorted.reverse)}
      yield coeff + "x^" + exp) mkString " + "
    }
  }

음. 다 좋은데 생성할 때 Map 을 주는 대신 여러개의 Pair 를 주고 Map 으로 바꾸면 좀 더 나을것 같다. 다음의 생성자를 추가하자. def + (other:Poly): Poly = new Poly((other.terms foldLeft terms)(addTerm)) def addTerm(ts: Map[Int, Double], t: (Int, Double)): Map[Int, Double] = { val (exp, coeff) = t ts + (exp -> (coeff + terms(exp))) }

def this(arg: (Int, Double)*) = this(arg.toMap)

그리고 ++ 대신 fold 를 이용하면 Map 을 생성하지 않고 바로 기존의 terms 에 원소를 추가하기 때문에 더 효율적이다.

    def + (other:Poly): Poly =
    new Poly((other.terms foldLeft terms)(addTerm))
    def addTerm(ts: Map[Int, Double], t: (Int, Double)): Map[Int, Double] = {
      val (exp, coeff) = t
      ts + (exp -> (coeff + terms(exp)))
    }

아래는 테스트 케이스

  "(x^2 + 3x) + (-2x + 7)" should "be x^2 + x + 7" in {
    val p1 = new Poly(2->1, 1->3)
    val p2 = new Poly(1->(-2), 0->7)
    val p3 = new Poly(2->1, 1->1, 0->7)

    assert((p1 + p2).terms == p3.terms)
  }

Putting the Pieces Together

이번엔 전화번호를 알파벳으로 바꾸는 예제를 통해서 스칼라의 컬렉션과 고차함수가 얼마나 expressive 한지 알아본다.

여기 나온 예제는 7 가지 언어로 이미 실험이 되었는데 스크립트 언어는 대략 100 라인, C 나 C++ 같은 언어는 대략 200-300 라인정도가 나왔다고 한다. (2000년)

  val mnem = Map(
    '2' -> "ABC",
    '3' -> "DEF",
    '4' -> "GHI",
    '5' -> "JKL",
    '6' -> "MNO",
    '7' -> "PQRS",
    '8' -> "TUV",
    '9' -> "WXYZ")

이런 맵이 있다고 하자. 7225247386 을 인코딩 하면 여러가지 경우가 나오겠지만, 그 중 하나는 SCALA IS FUN 이어야 한다. 교수님 센스보소

  val path = "/home/anster/github/coursera-scala/src/main/scala/coursera/chapter6/linux.words"
  val in = Source.fromFile(path)
  // java's iterator doesn't have groupBy
  val words = in.getLines.toList filter { _ forall { _.isLetter }}

  val mnem = Map(
    '2' -> "ABC",
    '3' -> "DEF",
    '4' -> "GHI",
    '5' -> "JKL",
    '6' -> "MNO",
    '7' -> "PQRS",
    '8' -> "TUV",
    '9' -> "WXYZ")

  // A to Z -> 2 to 9
  val charCode = mnem flatMap { case(k, v) => v map { c => (c, k) } }
  // or for ((digit, str) <- mnem; ltr <- str) yield ltr -> digit

  // "Java" -> "5282"
  def wordCode(word: String): String = word.toUpperCase map charCode

  // "5282" -> List("Java", "Kava", ...), "1111" -> List()
  val wordsForNum: Map[String, Seq[String]] =
    words groupBy wordCode withDefaultValue Seq()

  // return all ways to encode a number as a list of words
  def encode(number: String): Set[List[String]] =
    if (number.isEmpty) Set(List())
    else {
      (for {
        split <- 1 to number.length
        word <- wordsForNum(number take split)
        rest <- encode(number drop split)
      } yield word :: rest).toSet
    }

  def printEncoded(number: String) = {
    encode(number) map { _ mkString " "} map println
  }

  def translate(number: String): Set[String] = {
    encode(number) map { _ mkString " " }
  }

  translate("7225247386") foreach { println _ }

군더더기 없이 깔끔하다. 스칼라는 넉넉하게 50라인에서 끝납니다요

encode 가 좀 난해하긴 한데, 경우의 수를 모두 찾아내야 하므로 길이를 모두 짤라 wordForNum 에 넣고 각 길이마다 인코딩을 할 수 있는지 검사한 후 나머지도 encode 함수에 넣어 모든 경우의 수를 찾는다. 주의할 부분은 wordsForNum(number take split) 에서 없는 경우가 나올 수 있으니 withDefaultValue Seq() 로 처리하면 된다. 그리고 1 to number.length 가 Range 이기 때문에 리턴 타입이 IndexedSeq 다. 타입 에러를 해결하기 위해 toSet 을 사용한다.

Summary

마지막 6.7 Putting the Pieces Toghther 챕터를 보면서 스칼라는 정말 expressive 하다는걸 느낀다. 교수님 말로는 immutable collection 은

(1) easy to use: few steps to do the job
(2) concise: one word replaces a whole loop
(3) safe: type checker is really good at catching erros
(4) fast: collection ops are tuned, can be parallelized
(5) universal: one vocabulary to work on all kinds of collections

내 컴퓨터에서 돌아가는 SBT 를 보면 스칼라가 빠른지는 의문이지만

그리고 항상 느끼는 점이지만, Problem = Algorithm + Data Structure 다. 자료구조를 잘 선택하면 알고리즘이 간단해진다. 그래서 둘 다 배워야 하는거고 크흑

References

(1) http://docs.scala-lang.org

2014-10-25, Functional Programming in Scala, Coursera