Scala Easy Scalaz 5

Easy Scalaz 5

Yoneda, Coyoneda, Free and Trampoline

Free[F, A] 를 이용하면 Functor F 를 Monad 인스턴스로 만들 수 있습니다. 그런데, Coyoneda[G, A] 를 이용하면 아무 타입 G 나 Functor 인스턴스로 만들 수 있으므로 어떤 타입이든 (심지어 방금 만든 case class 조차) 모나드 인스턴스로 만들 수 있습니다.

Free 를 이용하면 사용자는 자신만의 Composable DSL 을 구성하고, 구성한 모나딕 연산을 실행하는 해석기를 작성하게 됩니다. 즉, 연산의 생성 과 연산의 실행 을 분리하여 다루게 됩니다. 이는 side-effect 를 실행 시점으로 미룰 수 있다는 뜻입니다. (실행용 해석기와 별도로 테스트용 해석기를 작성하는 것도 가능합니다)

그러면, 제가 가장 좋아하는 Programs as Values: Fure Functional JDBC Programming 예 로 시작해보겠습니다.

If We Have a Monad

JDBC 를 쌩으로 사용한다면, 다음과 같은 코드를 작성해야 할텐데

// ref - http://tpolecat.github.io/

case class Person(name: String, age: Int)

def getPerson(rs: ResultSet): Person {
  val name = rs.getString(1)
  val age  = rs.getInt(2)
}

다음과 같은 문제점이 있습니다.

managed resource 인 ResultSet 을 프로그래머가 다룰 수 있습니다. 어디에 저장이라도 하고 나중에 사용한다면 문제가 될 수 있습니다.
rs.get* 은 side-effect 를 만들어 내므로 테스트하기 쉽지 않습니다.

접근 방식을 바꿔보는건 어떨까요? 프로그램을 실행해서 side-effect 를 즉시 만드는 대신

어떤 연산을 수행할지를 case class 로 만들고 이것들을 조합해 어떤 연산을 수행할지 나타낸뒤에
연산의 조합을 번역해 실행하는 해석기(interpreter) 를 만들어 보겠습니다.

먼저 연산부터 정의하면,

sealed trait ResultSetOp[A]

final case class GetString(index: Int) extends ResultSetOp[String]
final case class GetInt(index: Int)    extends ResultSetOp[Int]
final case object Next                 extends ResultSetOp[Boolean]
final case object Close                extends ResultSetOp[Unit]

이 때 만약 ResultSetOp[A] 가 모나드라면 다음과 같이 작성할 수 있습니다.

def getPerson: ResultSetOp[Person] = for {
  name <- GetString(1)
  age  <- GetInt(2)
} yield Person(name, age)

// Application Operation `*>`  (e.g `1.some *> 2.some== 2.some)
// See, http://eed3si9n.com/learning-scalaz/Applicative.html
def getNextPerson: ResultSetOp[Person] =
  Next *> getPerson

def getPeople(n: Int): ResultSet[List[Person]] =
  getNextPerson.repicateM(n) // List.fill(n)(getNextPerson).sequence

def getAllPeople: ResultSetIO[Vector[Person]] =
  getPerson.whileM[Vector](Next)

ResultSetIO 는 모나드가 아니므로 위와 같이 작성할 수 없습니다.

Writing Your own DSL

놀랍게도, ResultSetIO 를 모나드로 만들 수 있습니다. flatMap, unit 구현 없이 얻을 수 있는 공짜 모나드입니다. 방법은 이렇습니다.

Free[F[_], ?] 는 Functor F 에 대해 Monad 입니다
Coyoneda[S[_], ?] 는 아무 타입 S 에 대해 Functor 입니다.

따라서 Free[Coyoneda[S, A], A 는 아무 타입 S 에 대해서 모나드입니다.

import scalaz.{Free, Coyoneda}, Free._

// ResultSetOpCoyo is the Functor
type ResultSetOpCoyo[A] = Coyoneda[ResultSetOp, A]

// ResultSetIO is the Monad
type ResultSetIO[A] = Free[ResultSetOpCoyo, A]

// same as
// type ResultSetIO2[A] = Free[({ type λ[α] = Coyoneda[ResultSetOp, α]})#λ, A]

따라서 다음처럼 작성할 수 있습니다.

val next                 : ResultSetIO[Boolean] = Free.liftFC(Next)
def getString(index: Int): ResultSetIO[String]  = Free.liftFC(GetString(index))
def getInt(index: Int)   : ResultSetIO[Int]     = Free.liftFC(GetInt(index))
def close                : ResultSetIO[Unit]    = Free.liftFC(Close)

여기서 Free.listFC 는 타입 ResultSetOp 를 바로 ResultSetIO 로 리프팅 해주는 헬퍼 함수입니다. (F = Free, C = Coyoneda)

// https://github.com/scalaz/scalaz/blob/series/7.2.x/core/src/main/scala/scalaz/Free.scala#L30

/** A version of `liftF` that infers the nested type constructor. */
def liftFU[MA](value: => MA)(implicit MA: Unapply[Functor, MA]): Free[MA.M, MA.A] =
  liftF(MA(value))(MA.TC)

/** A free monad over a free functor of `S`. */
def liftFC[S[_], A](s: S[A]): FreeC[S, A] =
    liftFU(Coyoneda lift s)

liftFU[MA] 에서, MA = Coyoneda[ResultSetOp, A] 로 보면 Free[MA.M, MA.A] 는 Free[Coyoneda[ResultSetOp, A], A] 가 됩니다. (Unapply.scala)

이를 이용해서 get* 를 작성해 보면

import scalaz._, Scalaz._

def getPerson: ResultSetIO[Person] = for {
  name <- getString(1)
  age  <- getInt(2)
} yield Person(name, age)

def getNextPerson: ResultSetIO[Person] =
  next *> getPerson

def getPeople(n: Int): ResultSetIO[List[Person]] =
  getNextPerson.replicateM(n) // List.fill(n)(getNextPerson).sequence

def getPersonOpt: ResultSetIO[Option[Person]] =
  next >>= {
    case true  => getPerson.map(_.some)
    case false => none.point[ResultSetIO]
  }

def getAllPeople: ResultSetIO[Vector[Person]] =
  getPerson.whileM[Vector](next)

DSL Interpreter

이제 RestSetOp 로 작성한 연산 (일종의 프로그램) 을 실행하려면, ResetSetOp 명령(case class) 을, 로직(side-effect 를 유발할 수 있는) 으로 변경해야 합니다.

NaturalTransformation 을 이용할건데, F ~> G 는 F 를 G 로 변경하는 변환(Transformation) 을 의미합니다.

// https://github.com/scalaz/scalaz/blob/series/7.2.x/core/src/main/scala/scalaz/package.scala#L113

/** A [[scalaz.NaturalTransformation]][F, G]. */
type ~>[-F[_], +G[_]] = NaturalTransformation[F, G]

// https://github.com/scalaz/scalaz/blob/series/7.2.x/core/src/main/scala/scalaz/NaturalTransformation.scala#L14
/** A universally quantified function, usually written as `F ~> G`,
  * for symmetry with `A => B`.
  *
  * Can be used to encode first-class functor transformations in the
  * same way functions encode first-class concrete value morphisms;
  * for example, `sequence` from [[scalaz.Traverse]] and `cosequence`
  * from [[scalaz.Distributive]] give rise to `([a]T[A[a]]) ~>
  * ([a]A[T[a]])`, for varying `A` and `T` constraints.
  */
trait NaturalTransformation[-F[_], +G[_]] {
  self =>
  def apply[A](fa: F[A]): G[A]

  def compose[E[_]](f: E ~> F): E ~> G = new (E ~> G) {
    def apply[A](ea: E[A]) = self(f(ea))
  }

  def andThen[H[_]](f: G ~> H): F ~> H =
    f compose self
}

이제, ResultSetOp 를 IO 로 변경하는 해석기를 작성하면, (Learning Scalaz - IO)

import scalaz.effect._

private def interpret(rs: ResultSet) = new (ResultSetOp ~> IO) {
    def apply[A](fa: ResultSetOp[A]): IO[A] = fa match {
      case Next         => IO(rs.next)
      case GetString(i) => IO(rs.getString(i))
      case GetInt(i)    => IO(rs.getInt(i))
      case Close        => IO(rs.close)
      // more...
    }
}

def run[A](a: ResultSetIO[A], rs: ResultSet): IO[A] =
  Free.runFC(a)(interpret(rs))

Why Free?

Free 가 제공하는 가치는 다음과 같습니다. (Ref - StackExchange)

It is a lightweight way of creating a domain-specific language that gives you an AST, and then having one or more interpreters to execute the AST however you like
The free monad part is just a handy way to get an AST that you can assemble using Haskell’s standard monad facilities (like do-notation) without having to write lots of custom code. This also ensures that your DSL is composable
You could then interpret this however you like: run it against a live database, run it against a mock, just log the commands for debugging or even try optimizing the queries

즉, Free 는 우리는 자신만의 Composable 한 DSL 을 구축하고, 필요에 따라 이 DSL 다른 방식으로 해석할 수 있도록 도와주는 도구입니다.

Free

(Free 와 Yoneda 는 난해할 수 있으니, Free 를 어떻게 사용하는지만 알고 싶다면 Reasonably Priced Monad 로 넘어가시면 됩니다.)

어떻게 F 가 Functor 이기만 하면 Free[F[_], ?] 가 모나드가 되는걸까요? 이를 알기 위해선, 모나드가 어떤 구조로 이루어져 있는지 알 필요가 있습니다.

Monad

A monad is just a monoid in the category of endofunctors, what’s the problem?

~~의사양반 이게 무슨소리요!~~

이제 Monoid 와 Functor 가 무엇인지 알아봅시다.

Monoid

어떤 합 S 에 대한 닫힌 연산 *, 집합 내의 어떤 원소 e 가 다음을 만족할 경우 모노이드라 부릅니다.

e * a = a = a * e (identity)
(a * b) * c = a * (b * c) (associativity)

일반적으로 e 를 항등원이라 부릅니다. Option[A] 도 None 을 항등원으로 사용하고, associativity 를 만족하는 A 의 연산을 사용하면 모노이드입니다. 따라서 A 가 모노이드면 Option[A] 도 모노이드입니다. (활용법은 Practical Scalaz 참조)

> load.ivy("org.scalaz" % "scalaz-core_2.11" % "7.2.0-M5")
> import scalaz._, Scalaz._


> 1.some |+| 2.some
res11: Option[Int] = Some(3)
> 1.some |+| none
res12: Option[Int] = Some(1)
> none[Int] |+| 1.some
res13: Option[Int] = Some(1)

Functor

Functor 는 일반적으로 다음처럼 정의되는데, 이는 Functor F 가 F 에서 값을 꺼내, 함수를 적용해 값을 변경할 수 있다는 것을 의미©니다.

A functor may go from one category to a different one

trait Functor[F[_]] {
  def map[A, B](fa: F[A])(f: A => B): F[B]
}

그리고 Functor 는 identity function 을 항등원으로 사용하면, 모노이드입니다.

F.map(x => x) == F
F map f map g == F map (f compose g)

이 때, 변환의 인풋과 아웃풋이 같은 카테고리라면 이 Functor 를 endo-functor 라 부릅니다.

A functor may go from one category to a different one, an endofunctor is a functor for which start and target category are the same.

Monad

그럼 다시 처음 문장으로 다시 돌아가면,

Monads are just monoids in the category of endofunctors

이 것의 의미를 이해하려면 모나드가 무엇인지 알아야 합니다.

trait Monad[F[_]] {
  def point[A](a: A): F[A]
  def join[A](ffa: F[F[A]): F[A]
  ...
}

일반적으로는 point (=return) 와 bind (= flatMap) 으로 모나드를 정의하나, join, map 으로도 bind 를 정할 수 있습니다.

// http://www.functionalvilnius.lt/meetups/meetups/2015-04-29-functional-vilnius-03/freemonads.pdf

trait Monad[F[_]] {
  def point[A](a: A): F[A]
  def bind[A, B](fa: F[A])(f: A => F[B]): F[B]

  def map[A, B](fa: F[A])(f: A => B): F[B] =
    bind(fa)(a => point(f(a))
  def join[A](ffa: F[F[A]): F[A] =
    bind(ffa)(fa => fa)
}

trait Monad[F[_]] {
  def map[A, B](fa: F[A])(f: A => B): F[B]
  def point[A](a: A): F[A]
  def join[A](ffa: F[F[A]): F[A] /* flatten*/

  def bind[A, B](fa: F[A])(f: A => F[B]): F[B] =
    join(map(fa)(f))
}

map, point, join 관점에서 모나드를 바라보면,

(endo)functor T : X → X
natural transformation μ : T × T → T (where × means functor composition (also known as join in Haskell)
natural transformation η : I → T (where I is the identity endofunctor on X also known as return in Haskell)

이때 위 연산들이 모노이드 법칙을 만족합니다.

e * a = a = a * e (identity)
(a * b) * c = a * (b * c) (associativity)
μ(η(T)) = T = μ(T(η)) (identity)
μ(μ(T × T) × T)) = μ(T × μ(T × T)) (associativity)

스칼라 코드로 보면,

> import scalaz._, Scalaz._

> val A = List(1, 2)
List[Int] = List(1, 2)

// identity left-side: μ(η(T)) = T
> A.map(x => Monad[List].point(x)).flatten
List[Int] = List(1, 2)

// identity right-side: μ(T(η)) = T
> Monad[List].point(A).flatten
List[Int] = List(1, 2)

// associativity
> val T = List(1, 2, 3, 4)
T: List[Int] = List(1, 2, 3, 4)
> val TT = T.map(List(_))
TT: List[List[Int]] = List(List(1), List(2), List(3), List(4))

// associativity left-side: μ(μ(T × T) × T))
> TT.flatten.map(List(_))
res30: List[List[Int]] = List(List(1), List(2), List(3), List(4))
> TT.flatten.map(List(_)).flatten
res31: List[Int] = List(1, 2, 3, 4)

// associativity right-side: μ(T × μ(T × T))
> List(TT.flatten)
res34: List[List[Int]] = List(List(1, 2, 3, 4))
> List(TT.flatten).flatten
res35: List[Int] = List(1, 2, 3, 4)

따라서 *Monad*는 (endo)Functor 카테고리에 대한 Monoid 입니다.

Free Monoid

Free Monad 가 bind, point 에 대한 구현 없이, 모나드가 되듯이 Free Monoid 또한 연산과 항등원에 대한 구현 없이 구조적 으로 모노이드입니다.

항등원과 연산을 Zero, Append 라는 이름으로 구조화 하면,

// http://www.functionalvilnius.lt/meetups/meetups/2015-04-29-functional-vilnius-03/freemonads.pdf

sealed trait FreeMonoid[+A]
final case object Zero extends FreeMonoid[Nothing]
final case class Value[A](a: A) extends FreeMonoid[A]
final case class Append[A](l: FreeMonoid[A], r: FreeMonoid[A]) extends FreeMonoid[A]

모노이드는 associativity 를 만족하므로, Append 를 우측 결합으로 바꾸고, Zero 로 끝나도록 하면

// http://www.functionalvilnius.lt/meetups/meetups/2015-04-29-functional-vilnius-03/freemonads.pdf

sealed trait FreeMonoid[+A]
final case object Zero extends FreeMonoid[Nothing]
final case class Append[A](l: A, r: FreeMonoid[A]) extends FreeMonoid[A]

List 와 동일한 구조임을 알 수 있습니다. 실제로, 리스트는 concatenation 연산, Nil 항등원에 대해 모노이드입니다.

Free Monad

이제까지의 내용을 정리하면

Monad is a monoid of functors
Then, Free Monad is a free Monoid of functors

따라서 Free Monad 는 Functor 의 List 라 볼 수 있습니다.

모나드의 point, join 을 구조화 (타입화) 하면,

def point[A](a: A): F[A]
def join[A, B](ffa: F[F[A]): F[A]

sealed trait Free[F[_], A]
case class Point[F[_], A](a: A) extends Free[F, A]             // == Return
case class Join[F[_], A](ffa: F[Free[F, A]]) extends Free[F, A] // == Suspend

map 을 타입화 하는 대신, F 가 Functor 라면 다음처럼 Free.point, Free.flatMap 을 작성할 수 있습니다.

sealed trait Free[F[_], A] {
  def point[F[_]](a: A): Free[F, A] = Point(a)
  def flatMap[B](f: A => Free[F, B])(implicit functor: Functor[F]): Free[F, B] =
    this match {
      case Point(a)  => f(a)
      case Join(ffa) => Join(ffa.map(fa => fa.flatMap(f)))
    }
  def map[B](f: A => B)(implicit functor: Functor[F]): Free[F, B] =
    flatMap(a => Point(f(a)))
}

case class Point[F[_], A](a: A) extends Free[F, A]
case class Join[F[_], A](ff: F[Free[F, A]]) extends Free[F, A]

fa.flatMap(f) 의 결과가 Free[F, B] 고 ffa.map 의 결과로 들어가므로, ffa.map(_ flatMap f) 의 결과는 F[Free[F, B] 입니다. 이걸 Free[F, B] 로 바꾸려면 Join 을 이용하면 됩니다.

이런 이유에서, F 가 Functor 면 Free[F, A] 는 Monad 입니다.

이제 리프팅과 실행을 위한 헬퍼 함수를 만들면,

// http://www.functionalvilnius.lt/meetups/meetups/2015-04-29-functional-vilnius-03/freemonads.pdf

import scalaz.{Functor, Monad, ~>}

def liftF[F[_], A](a: => F[A])(implicit F: Functor[F]): Free[F, A] =
  Join(F.map(a)(Point[F, A]))

def foldMap[F[_], M[_], A](fm: Free[F, A])(f: F ~> M)
                          (implicit FI: Functor[F], MI: Monad[M]): M[A] =
  fm match {
    case Point(a) => MI.pure(a)
    case Join(ffa) => MI.bind(f(ffa))(fa => foldMap(fa)(f))
  }

여기서 F ~> M 는 F 를 M 으로 변환해주는, NaturalTransformation 입니다.

// http://www.functionalvilnius.lt/meetups/meetups/2015-04-29-functional-vilnius-03/freemonads.pdf

type ~>[-F[_], +G[_]] = NaturalTransformation[F, G]

trait NaturalTransformation[-F[_], +G[_]] {
  self =>
  def apply[A](fa: F[A]): G[A]

  def compose[E[_]](f: E ~> F): E ~> G = new (E ~> G) {
    def apply[A](ea: E[A]) = self(f(ea))
  }
}

MI.bind(f(ffa)) 의 결과는 M[Free[F, A]] 이므로 여기에서 bind (= flatMap) 로 fa 를 얻어, 재귀적으로 foldMap 을 호출합니다.

Scalaz Free Implementation

def flatMap[B](f: A => Free[F, B])(implicit functor: Functor[F]): Free[F, B] =
    this match {
      case Point(a)  => f(a)
      case Join(ffa) => Join(ffa.map(fa => fa.flatMap(f)))
    }

Scalaz 에서는 flatMap 호출시 Stack 비용이 생각보다 크므로, flatMap 자체도 타입화하고 있습니다. 즉, Stack 대신에 Heap 을 사용합니다.

Point 대신, Return, Join 대신 Suspend, FlatMap 대신 GoSub 라는 타입 이름으로 구현되어 있습니다. (이해를 돕기 위해 7.x 대신, 6.0.4 버전을 차용)

// https://github.com/scalaz/scalaz/blob/release/6.0.4/core/src/main/scala/scalaz/Free.scala

final case class Return[S[+_], +A](a: A) extends Free[S, A]
final case class Suspend[S[+_], +A](a: S[Free[S, A]]) extends Free[S, A]
final case class Gosub[S[+_], A, +B](a: Free[S, A],
                                     f: A => Free[S, B]) extends Free[S, B]
sealed trait Free[S[+_], +A] {
  final def map[B](f: A => B): Free[S, B] =
    flatMap(a => Return(f(a)))

  final def flatMap[B](f: A => Free[S, B]): Free[S, B] = this match {
    case Gosub(a, g) => Gosub(a, (x: Any) => Gosub(g(x), f))
    case a           => Gosub(a, f)
  }
}

Trampoline

Free 를 이용하면, Stackoverflow 를 피할 수 있습니다. 이는 Free 가 flatMap 체인에서 스택 대신 힙을 이용하는 것을 응용한 것인데요,

// https://github.com/scalaz/scalaz/blob/release/6.0.4/core/src/main/scala/scalaz/Free.scala

/** A computation that can be stepped through, suspended, and paused */
type Trampoline[+A] = Free[Function0, A]

이때 Function0 도 Functor 이므로,

implicit Function0Functor: Functor[Function0] = new Functor[Function0] {
  def fmap[A, B](f: A => B)(fa: Function0[A]): Function0[B] =
    () => f(fa)
}

Free[Function0, A] 도 모나드입니다.

이제 스칼라에서 스택오버플로우가 발생하는 mutual recursion 코드를 만들어 보면,

// http://www.functionalvilnius.lt/meetups/meetups/2015-04-29-functional-vilnius-03/freemonads.pdf

def isOdd(n: Int): Boolean = {
  if (0 == n) false
  else isEven(n -1)
}

def isEven(n: Int): Boolean = {
  if (0 == n) true
  else isOdd(n -1)
}

isOdd(10000) // stackoverflow

이제 Trampoline 을 이용하면

// http://www.functionalvilnius.lt/meetups/meetups/2015-04-29-functional-vilnius-03/freemonads.pdf

import scalaz._, Scalaz._, Free._

def isOddT(n: Int): Trampoline[Boolean] =
  if (0 == n) return_(false)
  else suspend(isEvenT(n - 1))

def isEvenT(n: Int): Trampoline[Boolean] =
  if (0 == n) return_(true)
  else suspend(isOddT(n - 1))

scala> isOddT(2000000).run
res7: Boolean = false

scala> isOddT(2000001).run
res8: Boolean = true

return_ 과 suspend 는 다음처럼 정의되어 있습니다.

// https://github.com/scalaz/scalaz/blob/series/7.2.x/core/src/main/scala/scalaz/Free.scala#L15

trait FreeFunctions {

  ...
  def return_[S[_], A](value: => A)(implicit S: Applicative[S]): Free[S, A] =
    Suspend[S, A](S.point(Return[S, A](value)))

  def suspend[S[_], A](value: => Free[S, A])(implicit S: Applicative[S]): Free[S, A] =
    Suspend[S, A](S.point(value))

Yoneda, Coyoneda

포스트의 시작 부분에서 Coyoneda 에 대한 언급을 기억하시나요?

Free[F[_], ?] 는 Functor F 에 대해 Monad 입니다
Coyoneda[S[_], ?] 는 아무 타입에 대해 Functor 입니다.

Coyoneda 가 어떻게 Functor 를 만들어내는지 확인해 보겠습니다. 이 과정에서 dual 인 Yoneda 도 같이 살펴보겠습니다. (같은 Category 내에서, morphism 방향만 다른 경우)

먼저, Yoneda, Coyoneda 의 기본적인 내용을 훑고 가면

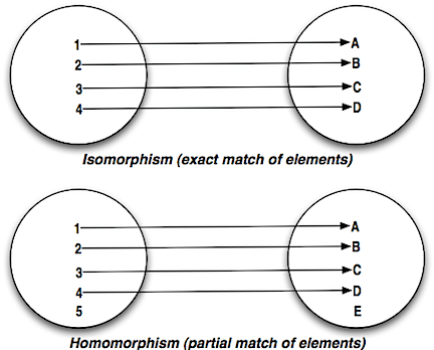
Yoneda, Coyoneda 는 Functor 입니다
Yoneda[F[_], A], Coyoneda[F[_], A] 는 F[A] 와 isomorphic 입니다 (F 가 Functor 일 경우)
Yoneda[F, A] 에서 F[A] 로의 homomorphism 은 F 가 Functor 가 아닐 경우에도 존재합니다
F[A] 에서 Coyoneda[F, A] 로의 homomorphism 은 F 가 Functor 가 아닐 경우에도 존재합니다 (중요)
Yoneda, Coyoneda 모두 Functor 가 필요한 시점을 미루³ , Functor.map 의 체인을, 일반 함수의 체인으로 표현합니다. 결국엔 Functor 가 필요합니다 (중요)

(Image - http://evolvingthoughts.net/2010/08/homology-and-analogy/)

즉 Coyoneda[F[_], A] 가 F 와 상관없이 Functor 인 이유는, F[A] -> Coyoenda[F[_], A] 로의 변환이 F Functor 인 것과 상관이 없으며 Coyoneda 자체가 Functor 인스턴스이기 때문입니다.

추상은 간단합니다. Functor[F] 가 F[A] -> F[B] 로의 변환을 f: A => B 만 가지고 해 낼 수 있다는 점을 역이용하면 됩니다. F[A] 에 Functor.map(f) 를 적용하는 것이 아니라, 값 A 가 있을 때 f(a) 를 적용한 뒤에, F[B] 를 만들면 됩니다. 다시 말해

Functor[F] 는 F[A] 와 f: A => B, g: B = > C 가 가 있을 때 Functor[F].map(f compose g) 대신
f compose g 를 먼저 하고, 이것의 결과값인 C 를 이용해 F[C] 를 만들면 됩니다. 그러면 Functor[F].map 연산을 함수의 컴포지션으로 해결할 수 있습니다.

Yoneda

// https://github.com/scalaz/scalaz/blob/series/7.1.x/core/src/main/scala/scalaz/Yoneda.scala

abstract class Yoneda[F[_], A] { yo =>
  def apply[B](f: A => B): F[B]

  def run: F[A] = apply(a => a)

  def map[B](f: A => B): Yoneda[F, B] = new Yoneda[F, B] {
    override def apply[C](g: (B) => C): F[C] = yo(f andThen g)
  }
}

/** `F[A]` converts to `Yoneda[F, A]` for any functor `F` */
def apply[F[_]: Functor, A](fa: F[A]): Yoneda[F, A] = new Yoneda[F, A] {
  override def apply[B](f: A => B): F[B] = Functor[F].map(fa)(f)
}

/** `Yoneda[F, A]` converts to `F[A` for any `F` */
def from[F[_], A](yo: Yoneda[F, A]): F[A] =
  yo.run

/** `Yoneda[F, _]` is a functor for any `F` */
implicit def yonedaFunctor[F[_]]: Functor[({ type  λ[α] = Yoneda[F,α]})#λ] =
  new Functor[({type λ[α] = Yoneda[F, α]})#λ] {
    override def map[A, B](ya: Yoneda[F, A])(f: A => B): Yoneda[F, B] =
      ya map f
  }

Yoneda[F[_], ?] 는 그 자체로 Functor 이나 이를 만들기 위해선 F 가 Functor 여야 합니다. 반면 Yoneda[F, A] -> F[A] 로의 변환은 F 가 Functor 이던 아니던 상관 없습니다.

Coyoneda

그렇다면, dual 인 Coyoneda 는 어떨까요? Yoneda F[A] 를 Functor 로 부터 얻는것이 아니라, Identity 를 이용해, 처음부터 F[A] 를 가지고 있습니다. 이로 부터 얻어지는 결론은 놀랍습니다.

sealed abstract class Coyoneda[F[_], A] { coyo =>
  type I
  val fi: F[I]
  val k: I => A

  final def map[B](f: A => B): Aux[F, I, B] =
    apply(fi)(f compose k)

  final def run(implicit F: Functor[F]): F[A] =
    F.map(fi)(k)
}

type Aux[F[_], A, B] = Coyoneda[F, B] { type I = A }

def apply[F[_], A, B](fa: F[A])(_k: A => B): Aux[F, A, B] =
  new Coyoneda[F, B] {
    type I = A
    val k = _k
    val fi = fa
  }

/** `F[A]` converts to `Coyoneda[F, A]` for any `F` */
def lift[F[_], A](fa: F[A]): Coyoneda[F, A] = apply(fa)(identity[A])

/** `Coyoneda[F, A]` converts to `F[A]` for any Functor `F` */
def from[F[_], A](coyo: Coyoneda[F, A])(implicit F: Functor[F]): F[A] =
  F.map(coyo.fi)(coyo.k)

/** `CoyoYoneda[F, _]` is a functor for any `F` */
implicit def coyonedaFunctor[F[_]]: Functor[({ type  λ[α] = Coyoneda[F,α]})#λ] =
  new Functor[({type λ[α] = Coyoneda[F, α]})#λ] {
    override def map[A, B](ca: Coyoneda[F, A])(f: A => B): Coyoneda[F, B] =
      ca.map(f)
  }

따라서 Coyoneda[F[_], ?] 를 만들기 위해서 F 가 Functor 일 필요가 없습니다.

Stackoverflow - The Power of (Co)yoneda 에선 다음처럼 설명합니다.

newtype Yoneda f a = Yoneda { runYoneda :: forall b . (a -> b) -> f b }

instance Functor (Yoneda f) where
  fmap f y = Yoneda (\ab -> runYoneda y (ab . f))

data CoYoneda f a = forall b . CoYoneda (b -> a) (f b)

instance Functor (CoYoneda f) where
  fmap f (CoYoneda mp fb) = CoYoneda (f . mp) fb

So instead of appealing to the Functor instance for f during definition of the Functor instance for Yoneda, it gets “defered” to the construction of the Yoneda itself. Computationally, it also has the nice property of turning all fmaps into compositions with the “continuation” function (a -> b).

The opposite occurs in CoYoneda. For instance, CoYoneda f is still a Functor whether or not f is. Also we again notice the property that fmap is nothing more than composition along the eventual continuation.

So both of these are a way of “ignoring” a Functor requirement for a little while, especially while performing fmaps.

Reasonably Priced Monad

for comprehension 내에서는 단 하나의 모나드 밖에 쓸 수 없습니다. ~~단칸방 세입자 모나드~~ Monad Transformer 등을 사용하긴 하는데 ¶편하기 짝이 없지요.

Rúnar Bjarnason 은 Composable application architecture with reasonably priced monads 에서 Coproduct 를 이용해 Free 를 조합하는 법을 소개합니다. (이 비디오는 꼭 보셔야합니다!)

요약하면 Free 를 이용해 생성한 서로 다른 두개의 모나드는 같은 for comprehension 내에서 사용할 수 없습니다. 이 때 Coproduct 를 이용해서 하나의 타입으로 묶고, 타입 자동 주입을 위해 Inject 를 이용하면 많은 코드 없이도, 편리하게 Free 를 이용할 수 있다는 것입니다.

예를 들어 다음과 처럼 두개의 프리 모나드 Interact, Auth 가 있을 때

// Interact
trait InteractOp[A]
final case class Ask(prompt: String) extends InteractOp[String]
final case class Tell(msg: String)   extends InteractOp[Unit]

type CoyonedaInteract[A] = Coyoneda[InteractOp, A]
type Interact[A] = Free[CoyonedaInteract, A]

def ask(prompt: String) = liftFC(Ask(prompt))
def tell(msg: String) = liftFC(Tell(msg))

// Auth
case class User(userId: UserId, permissions: Set[Permission])

sealed trait AuthOp[A]
final case class Login(userId: UserId, password: Password) extends AuthOp[Option[User]]
final case class HasPermission(user: User, permission: Permission) extends AuthOp[Boolean]

type CoyonedaAuth[A] = Coyoneda[AuthOp, A]
type Auth[A] = Free[CoyonedaAuth, A]

def login(userId: UserId, password: Password): FreeC[F, Option[User]] =
  liftFC(Login(userId, password))

def hasPermission(user: User, permission: Permission): FreeC[F, Boolean] =
  liftFC(HasPermission(user, permission))

// Log

sealed trait LogOp[A]
final case class Warn(message: String)  extends LogOp[Unit]
final case class Error(message: String) extends LogOp[Unit]
final case class Info(message: String)  extends LogOp[Unit]

type CoyonedaLog[A] = Coyoneda[LogOp, A]
type Log[A] = Free[CoyonedaLog, A]

object Log {
  def warn(message: String)  = liftFC(Warn(message))
  def info(message: String)  = liftFC(Info(message))
  def error(message: String) = liftFC(Error(message))

다음처럼 같은 for comprehension 구문에서 사용할 수 없습니다.

// doesn't compile

for {
  userId <- ask("Insert User ID: ")
  password <- ask("Password: ")
  user <- login(userId, password)
  _ <- info(s"user $userId logged in")
  hasPermission <- user.cata(
    none = point(false),
    some = hasPermission(_, "scalaz repository")
  )
  _ <- warn(s"$userId has no permission for scalaz repository")
} yield hasPermission

이 때 Coproduct 를 이용하면, 가능합니다.

// combine free monads
type Language0[A] = Coproduct[InteractOp, AuthOp, A]
type Language[A] = Coproduct[LogOp, Language0, A]
type LanguageCoyo[A] = Coyoneda[Language, A]
type LanguageMonad[A] = Free[LanguageCoyo, A]
def point[A](a: => A): FreeC[Language, A] = Monad[LanguageMonad].point(a)

// combine interpreters
val interpreter0: Language0 ~> Id = or(InteractInterpreter, AuthInterpreter)
val interpreter: Language ~> Id = or(LogInterpreter, interpreter0)

// run a program
def main(args: Array[String]) {
  def program(implicit I: Interact[Language], A: Auth[Language], L: Log[Language]) = {
    import I._, A._, L._

    for {
      userId <- ask("Insert User ID: ")
      password <- ask("Password: ")
      user <- login(userId, password)
      _ <- info(s"user $userId logged in")
      hasPermission <- user.cata(
        none = point(false),
        some = hasPermission(_, "scalaz repository")
      )
      _ <- warn(s"$userId has no permission for scalaz repository")
    } yield hasPermission
  }

  program.mapSuspension(Coyoneda.liftTF(interpreter))
}

여기서 or 과 lift 는 라이브러리 코드라 생각하시면 됩니다. 이제 변화된 프리 모나드 부분을 보면,

object Auth {
  type UserId = String
  type Password = String
  type Permission = String

  implicit def instance[F[_]](implicit I: Inject[AuthOp, F]): Auth[F] =
    new Auth
}

class Auth[F[_]](implicit I: Inject[AuthOp, F]) {
  import Common._
  def login(userId: UserId, password: Password): FreeC[F, Option[User]] =
    lift(Login(userId, password))

  def hasPermission(user: User, permission: Permission): FreeC[F, Boolean] =
    lift(HasPermission(user, permission))
}

class Interact[F[_]](implicit I: Inject[InteractOp, F]) {
  import Common._

  def ask(prompt: String): FreeC[F, String] =
    lift(Ask(prompt))

  def tell(message: String): FreeC[F, Unit] =
    lift(Tell(message))
}

object Interact {
  implicit def instance[F[_]](implicit I: Inject[InteractOp, F]): Interact[F] =
    new Interact
}

class Log[F[_]](implicit I: Inject[LogOp, F]) {
  import Common._

  def warn(message: String)  = lift(Warn(message))
  def info(message: String)  = lift(Info(message))
  def error(message: String) = lift(Error(message))
}

object Log {
  implicit def instant[F[_]](implicit I: Inject[LogOp ,F]) =
    new Log
}

이제, Common 을 보면

object Common {
  import scalaz.Coproduct, scalaz.~>

  def or[F[_], G[_], H[_]](f: F ~> H, g: G ~> H): ({type cp[α] = Coproduct[F,G,α]})#cp ~> H =
    new NaturalTransformation[({type cp[α] = Coproduct[F,G,α]})#cp,H] {
      def apply[A](fa: Coproduct[F,G,A]): H[A] = fa.run match {
        case -\/(ff) ⇒ f(ff)
        case \/-(gg) ⇒ g(gg)
      }
    }

  def lift[F[_], G[_], A](fa: F[A])(implicit I: Inject[F, G]): FreeC[G, A] =
    Free.liftFC(I.inj(fa))
}

Coproduct[F, G, A] 는 둘 중 하나 를 의미하는 추상입니다. 결과로 F[A] \/ G[A] (scalaz either) 을 돌려줍니다.

// https://github.com/scalaz/scalaz/blob/series/7.2.x/core/src/main/scala/scalaz/Coproduct.scala

final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A]) {
  ...
}

trait CoproductFunctions {
  def leftc[F[_], G[_], A](x: F[A]): Coproduct[F, G, A] =
    Coproduct(-\/(x))

  def rightc[F[_], G[_], A](x: G[A]): Coproduct[F, G, A] =
    Coproduct(\/-(x))

  ...
}

Inject[F[_], G[_]] 는 F, G 를 포함하는 더 큰 타입인 Coproduct 를 만들때 쓰입니다.

def lift[F[_], G[_], A](fa: F[A])(implicit I: Inject[F, G]): FreeC[G, A] =
  Free.liftFC(I.inj(fa))

// F == Langauge
class Log[F[_]](implicit I: Inject[LogOp, F]) {
  def warn(message: String)  = lift(Warn(message))
  def info(message: String)  = lift(Info(message))
  def error(message: String) = lift(Error(message))
}

Inject 는 이렇게 생겼습니다.

// https://github.com/scalaz/scalaz/blob/series/7.2.x/core/src/main/scala/scalaz/Inject.scala

sealed abstract class Inject[F[_], G[_]] {
  def inj[A](fa: F[A]): G[A]
  def prj[A](ga: G[A]): Option[F[A]]
}

sealed abstract class InjectInstances {
  implicit def reflexiveInjectInstance[F[_]] =
    new Inject[F, F] {
      def inj[A](fa: F[A]) = fa
      def prj[A](ga: F[A]) = some(ga)
    }

  implicit def leftInjectInstance[F[_], G[_]] =
    new Inject[F, ({type λ[α] = Coproduct[F, G, α]})#λ] {
      def inj[A](fa: F[A]) = Coproduct.leftc(fa)
      def prj[A](ga: Coproduct[F, G, A]) = ga.run.fold(some(_), _ => none)
    }

  implicit def rightInjectInstance[F[_], G[_], H[_]](implicit I: Inject[F, G]) =
      new Inject[F, ({type λ[α] = Coproduct[H, G, α]})#λ] {
        def inj[A](fa: F[A]) = Coproduct.rightc(I.inj(fa))
        def prj[A](ga: Coproduct[H, G, A]) = ga.run.fold(_ => none, I.prj(_))
      }
}

따라서 F, G 타입만 맞추어 주면 Inject 인스턴스는 자동으로 생성됩니다.

다음시간에는 side-effect 의 세계로 넘어가 ST, IO 등을 살펴보겠습니다.

Easy Scalaz 5

Yoneda, Coyoneda, Free and Trampoline

If We Have a Monad

Writing Your own DSL

DSL Interpreter

Why Free?

Free

Monad

Monoid

Functor

Monad

Free Monoid

Free Monad

Scalaz Free Implementation

Trampoline

Yoneda, Coyoneda

Yoneda

Coyoneda

Reasonably Priced Monad

Previous Posts

References