Haskell 하스켈로 배우는 함수형 언어 9

하스켈로 배우는 함수형 언어 9

Intro

이번시간엔 함수형 프로그래밍에서 property 를 증명하는 방법인 induction 에 대해 배워보고, 하스켈에서 알고리즘의 성능이 어떨까에 대해 좀 논의해 보겠습니다. 마지막엔 Rose Tree 를 구현하면서 Functor, Monoid, Foldable 등에 대해 좀 알아봅시다.

수학에서 다음 두 식은 똑같습니다.

xz + yz = (x + y)z

근데, 잘 보면 연산의 수가 다릅니다. 좌측은 3개고, 우측은 2개면 되지요. 하스켈에서도 이런 생각들을 좀 해봅시다. built-in 연산자에 대해서뿐만 아니라, user-defined 연산자 (함수) 에 대해서도 생각할 수 있으니까, 좀 다양하겠네요.

Reasoning about Haskell

double :: Int -> Int
double x = x + x

이제 모든 x + x 는 double x 로, 바꿀 수 있죠. 그 반대도 가능하고요. 근데, multiple equations 를 쓰면 좀 얘기가 다릅니다.

isZero :: Int -> Bool
isZero 0 = True
isZero n = False

첫번째 식 isZero 0 = True 는 어느 방향으로든 자유롭게 적용가능하지만, 두번째는 아닙니다. 사실은 이런 뜻이거든요

isZero 0          = True
isZero n | n /= 0 = False

이제 좌우를 쉽게 치환할 수 있습니다. 이렇게 식의 순서에 의존하지 않는 패턴을 disjoint 혹은 non-overlapping 이라 부릅니다.

Patterns that do not rely on the order in which the are matched are called disjoint or non-overlapping

프로그램에 대해서 reasoning 할 땐 가능하면 non-overlapping 패턴을 사용하는게 좋습니다. standard library 에 있는 대부분의 함수들은 이런식으로 작성 되어있습니다.

Simple examples

reverse :: [a] -> [a]
reverse [] = []
reverse (x:xs) reverse xs ++ [x]

이 구현을 보면 reverse [x] = [x] 입니다. 근데, 이걸 연산하려면

reverse [x]
reverse (x:[])
reverse [] ++ [x]
[] ++ [x]
[x]

따라서 reverse [x] = [x] 를 추가해서 효율적인 구현을 할 수 있습니다.

Induction on numbers

함수형 프로그램은 종종 재귀를 이용해 작성되는데, 여기에 induction 을 이용할 수 있습니다. 예전에 본 자연수 타입 Nat 의 정의를 떠올려 보면

data Nat = Zero | Succ Nat

어떤 유한한 수에 대해서 어떤 property p 를 증명하려고 할 때, 먼저 base case 인 Zero 에 대해 보이고, inductive case Succ 에 대해서 보이면 됩니다. 더 자세히는, 어떤 자연수 n 에 대해서 p 가 참일때 (induction hypothesis), Succ n 에 대해서도 참임을 보이면 됩니다.

구체적인 예제를 보도록 하죠. 두 Nat 를 더해 Nat 를 만드는 add 함수를 만들면

add :: Nat -> Nat -> Nat
add Zero m = m
add (Succ n) m = Succ (add n m)

첫 번째씩 add Zero m = m 은 모든 자연수 m 에 대해 참이기 때문에, add n Zero = n 을 증명하겠습니다. 이걸 가설 p 라 부릅시다.

(1) base case

add Zero Zero
Zero

(2) inductive case

이 단계에서는 p 가 자연수 n 에 대해 참일때 p (Succ n) 이 참임을 보이면 됩니다. 다시 말해 가설 p add n Zero = n 을 이용해 add (Succ n) Zero = Succ n 임을 보여야 합니다.

add (Succ n) Zero -- should be `Succ n`

= Succ (add n Zero) 

= Succ n -- by induction hypothesis

다른 속성으로 associativity 를 증명할 수도 있습니다.

add x (add y z) = add (add x y) z

인자가 3개인데 무엇부터 시작해야 할까요? add 는 패턴매칭을 이용해 작성되었고, 재귀 부분이 첫번째 인자를 주로 이용하므로 x 를 선택하는게 자연스러울 겁니다. y는 1 번 쓰이고, z는 첫번째 인자로 한번도 안쓰이네요.

(1) base case

add Zero (y z) -- should be `add (add Zero y) z`

= add y z
= add (add Zero y) z -- unapplying add

(2) inductive case

p 는 `add x (add y z) = add (add x y) z

add (Succ x) (add y z) -- should be 'add (add (Succ x) y) z`

= Succ (add x (add y z)) -- apply outer add
= Succ (add (add x y) z) -- induction hypothesis
= add (Succ (add x y) z) -- unapply outer add
= add (add (Succ x) y) z -- unapply inner add

이렇게 unapply, apply 를 편하게 할 수 있는 이유는 위에서 add 를 non-overlapping 패턴으로 작성했기 때문이지요.

induction 을 recursive type 인 Nat 에 적용했지만, Integer 타입에도 적용할 수 있습니다.

어떤 property p 를 n >= 0 에 대해 증명하려고 할 때는 먼저 base case 인 0 에 대해 참임을 보이고, n >= 0 일때, n + 1 에 대해서도 참임을 보이면 됩니다.

replicate :: Int -> a -> [a]
replicate 0 _       = []
replicate (n + 1) x = x : replicate n x
-- replicate n x = x : replicate (n - 1) x

요즘 컴파일러는 n + 1 패턴을 막아서 아마 주석처리부분처럼 작성해야 합니다. 무튼 저 정의대로만 보면, n 에 대해 참일때 n + 1 일때도 참임을 보이는건 정말 쉽습니다. 정의 그 자체가 induction 이니까요.

Induction on lists

재귀는 자연수에만 쓸 수 있는건 아니고, 리스트와 같은 다양한 재귀적인 타입에 사용할 수 있습니다. base case 는 [] 이 되겠고, successor function 은 : 이 되겠네요.

그러므로 리스트에 대해 어떤 property p 를 증명하려면, 먼저 [] 에 대해 참임을 보이고 p xs 가 참일때 p x:xs 가 참임을 보이면 됩니다. ~~참 쉽죠?~~

reverse 연산에 대해 reverse (reverse xs) = xs 를 증명해 봅시다.

(1) base case

reverse (reverse []) -- should be '[]'

= reverse []
= []

(2) inductive case

-- induction hypothesis

reverse (reverse xs) = xs

증명은

reverse (reverse x:xs) -- = x:xs

= reverse (reverse xs ++ [x])
= reverse [x] ++ reverse (reverse xs) -- by distributivity
= [x] ++ xs -- induction hypothesis
= x:xs

여기서 사용한 성질중에 하나가 distributivity 인데,

-- induction hypothesis
reverse (xs ++ ys) = reverse ys ++ reverse xs

(1) base-case

reverse ([] ++ ys) -- reverse ys ++ reverse [] 

= reverse ys
= [] ++ reverse ys -- unapply ++
= reverse [] ++ reverse ys

(2) inductive case

reverse ((x:xs) ++ ys) -- reverse ys ++ reverse (x:xs)

= reverse (x:(xs ++ ys))
= reverse (xs ++ ys) ++ [x]
= reverse ys ++ (reverse xs ++ [x])
= reverse ys ++ (reverse (x:xs)) -- unapply second reverse

이 증명은 ++ 가 associative 라는 사실을 이용해 증명했는데, 이것도 마찬가지로 증명할 수 있습니다.

Marking append vanish

많은 재귀 함수들이 ++ 연산을 이용해 작성되었는데, 편하긴 하지만 재귀적으로 사용되면 비용이 좀 듭니다. 따라서 이번에는 ++ 를 제거 해서 좀 더 효율적으로 함수를 작성해봅시다.

reverse 함수부터 해 보면

reverse :: [a] -> [a]
reverse [] = []
reverse (x:xs) = reverse xs ++ [x]

이렇게 작성된 reverse 함수의 성능은 어떨까요? 먼저 생각해 볼 것은 xs ++ ys 을 evaluation 하기 위해 얼마의 스텝이 필요할까? 입니다. xs ++ ys 는 xs 를 쪼개가면서 xs 에 붙이기 때문에, xs + 1 만큼의 스텝이 필요하죠.

참고로 append 의 정의는

append :: [a] -> [a] -> [a] 
append [ ] xs    = xs
append (x:xs) ys = x : append xs ys

좀 간단히 생각하기 위해 xs, ys 가 fully evaluated 되었다 합시다. 그 결과로 ++ 는 첫 번째 인자 xs 의 길이에 비례하는 linear time 퍼포먼스를 보여줍니다.

결과적으로 reverse xs 의 성능은, 길이를 n 이라 했을 때 1 + 2 + ... + n + 1 입니다. (n^2 + 3n + 2) / 2 겠네요. 이는 reverse 함수가 quadratic time 의 함수라는걸 말해줍니다. 1000 개를 뒤집으려면, 10000000 번만큼 연산을 해야한다는 소리지요.

다행히도 induction 을 이용해 쓸모없는 ++ 부분을 제거하고, 성능을 개선할 수 있습니다.

reverse 와 ++ 를 합친 좀 더 general 한 함수를 만듭시다. reverse' 라 부를건데, reverse xs += ys 와 같은 일을 할겁니다.

reverse' xs ys -- = reverse xs ++ ys

이렇게 만들면 reverse 자체는 이렇게 정의할 수 있습니다. [] 가 append 를 위한 identity 라는 점을 이용한 것이지요.

reverse xs = reverse' xs []

신기하게도 이 속성을 증명하면서, 이 reverse' 의 정의 자체를 얻을 수 있습니다.

(1) base case

reverse' [] ys 

= reverse [] ++ ys 
= [] ++ ys
= ys

(2) inductive case

reverse' (x:xs) ys

= reverse (x:xs) ++ ys
= (reverse xs ++ [x]) ++ ys
= reverse xs ++ ([x] ++ ys]) -- by associativity of ++
= reverse' xs ([x] ++ ys) -- by induction hypothesis
= reverse' xs (x:ys)

따라서 reverse' 의 정의는

reverse' [a] -> [a] -> [a]
reverse' [] y = ys
reverse' (x:xs) ys = reverse' xs (x:ys)

아까 언급했던대로 reverse 를 다시 만들면

reverse :: [a] -> [a]
reverse xs = reverse' xs []

이제는 x:ys 처럼, 하나씩 분리해 나가면서 붙기때문에 성능이더 빠릅니다. 정확히는 n + 2 연산이 필요하지요. linear time 입니다.

사실은 7장 에서 이미 개선된 reverse 를 봤었습니다. reverse = foldl (:) [] 기억 나시나요?

flatten

data Tree = Leaf Int | Node Tree Tree
flatten :: Tree -> [Int]
flatten (Leaf n) = [n]
flatten (Node l r) = flatten l ++ flatten r

이 flatten 도 ++ 때문에 느립니다. 위 reverse 처럼 개선해 보면

flatten' t ns = flatten t ++ [ns]

(1) base case

flatten' (Leaf n) ns

= flatten (Leaf n) ++ ns
= [n] ++ ns
n:ns

(2) inductive case

flatten' (Node l r) ns

= (flatten l ++ flatten r) ++ ns
= flatten l ++ (flatten r ++ ns) -- associativity
= flatten' l ++ (faltten r ++ ns) -- hypothesis
= flatten' l (flatten' r ns)

따라서 flatten', flatten 은

flatten' :: Tree -> [Int] -> [Int]
flatten' (Leaf n) ns = n:ns
flatten' (Node l r) ns = flatten' l (flatten' r ns)

flatten :: Tree -> [Int]
flatten t = flatten' t []

Compiler Correctness

data Expr = Val Int | Add Expr Expr

eval :: Expr -> Int
eval (Val n) = n
eval (Add x y) = eval x + eval y

지난번에 만들었던 이 계산 기계를 잘 보면, expression 이 간접적으로 evaluated 됩니다. 스택을 이용해 실행되는 코드의 도움을 받아서요.

자세히 보면 스택은 integer list 고, 코드는 push, add 연산의 리스트입니다. 따라서

type Stack = [Int]
type Code = [Op]
data Op = PUSH Int | ADD

결국 코드를 실행한다는 말은 초기 스택을 받아, 이걸 이용해 계산을 하고 다시 스택을 돌려준다는 뜻입니다.

exec :: Code -> Stack -> Stack
exec []         s       = s
exec (PUSH n:c) s       = exec c (n:s)
exec (ADD:c)    (m:n:s) = exec c (m+n:s)

이제 Expr 을 Code 로 변경하는 함수 compile 를 만들면

compile' :: Expr -> Code
compile' (Val n) = [PUSH n]
compile' (Add x y) = compile x ++ compile y ++ [ADD]

compile :: Expr -> Code
compile e = compile' e

그리고 화면에 출력을 위해 Show 를 구현하고 샘플식 e 를 만들면

instance Show Expr where
  show (Val n) = "(Val " ++ show n ++ ")"
  show (Add x y) = "(Add " ++ show x ++ " " ++ show y ++ ")"

instance Show Op where
  show (PUSH n) = "(PUSH " ++ show n ++ ")"
  show (ADD) = "(ADD)"

e :: Expr
e = (Add (Add (Val 2) (Val 3)) (Val 4))

> e
-- (Add (Add (Val 2) (Val 3)) (Val 4))

> eval e
-- 9

> compile e
-- [(PUSH 2),(PUSH 3),(ADD),(PUSH 4),(ADD)]

잘 보면, 식을 컴파일해서 초기스택 [] 와 함께 실행시킨 것은, [eval e] 와 같다는 것을 알 수 있지요. [] 대신 임의의 스택 s 를 이용하면

exec (compile e) s = eval e:s

(1) base-case: (Val n)

exec (compile (Val n)) s

= exec [PUSH n] s
= n : s
eval (Val n) : s -- unapply eval

(2) inductive case: (Add x y)

exec (compile (Add x y)) s

= exec (compile x ++ compile y ++ [ADD]) s
= exec (compile x ++ (compile y ++ [ADD])) s -- associativity
= exec (compile y ++ [ADD]) (exec (compile x) s) -- distributivity of exec
= exec (compile y ++ [ADD]) (eval x:s) -- induction hypothesis for x
= exec [ADD] (exec (compile y) (eval x:s)) -- distributivity
= exec [ADD] (eval y : eval x : s)
= (eval x + eval y) : s -- apply exec
= eval (Add x y) : s -- unapply eval

위에서 쓴 exec 의 distributivity 를 보이면

exec (c ++ d) s = exec d (exec c s)

c 가 PUSH 일때, 그리고 ADD 일때로 나눠서 증명하면 되죠.

(1) base case

exec ([] ++ d) s 

= exec d s
= exec d (exec [] s) -- unapply exec

(2-1) inductive case: PUSH n

exec ((PUSH n : c) ++ d) s

= exec (PUSH n : (c ++ d)) s
= exec (c ++ d) (n:s)
= exec d (exec c (n:s)) -- induction hypothesis
= exec d (exec (PUSH n:c) s) -- unapply exec

(2-2) inductive case: ADD

exec ((ADD : c) ++ d) s
= exec (ADD : (c ++ d)) s
= exec (ADD : (c ++ d)) (m:n:s') -- assume s == m:n:s'
= exec (c ++ d) (m+n:s') -- apply exec
= exec d (exec c (m+n:s')) -- induction hypothesis
= exec d (exec (ADD : c) (m:n:s')) -- unapply exec
= exec d (exec (ADD : c) s)

s 를 m:n:s' 로 의 가정은 underflow error 를 겪을 수 있는것처럼 보이지만, 실제로는 그렇지 않습니다. 왜냐하면 ADD 연산이 들어있다는 자체가 최소한 두개의 숫자는 스택에 포함한다는 뜻이기 때문입니다. (exec 의 정의를 보세요)

그리고 이전 장에서 append 연산에 적용했던 테크닉을 다시 가져와서, distributivity property 의 underflow 이슈를 예방할 수 있습니다. 이 속성을 유지하도록 하면요

compile' e c = compile e ++ c

이 속성을 induction 을 이용해서 차근차근 풀면, 아래와 같은 정의를 얻을 수 있습니다.

compile' :: Expr -> Code -> Code
compile' (Val n) c = PUSH n : c
compile' (Add x y) = compile' x (compile' y (ADD : c))

compile e = compile' e []

그러면 compiler correctness 는

exec (compiler' e c) s = exec c (eval e : s)

해석은 원문을 첨부하겠습니다.

That is, compiling an expression and then executing the resulting code together with arbitrary additional code gives the same result as executing the additional code with the value of the expression on top of the original stack

Note that with s = c = [ ], this new result simplifies to exec (compile e) [] = [eval e], our original statement of correctness.

In addition to avoiding the problem of stack underflow in the correctness proof, the accumulator version of the compiler has two further benefits.

First of all, it avoids the use of ++, and is hence more efficient. And,

secondly, the new proof is less than half the combined length of our previous two proofs. As is often the case in formal reasoning, generalising a result in the appropriate manner can considerably simplify its proof. Mathematics is an excellent tool for guiding the development of efficient programs with simple proofs!

Rose Tree

로즈 트리는 원소의 개수가 unbounded 인 트리입니다. 이렇게 정의할 수 있습니다.

data a = a :> [Rose a] deriving Show

여기서 :> 는 constructor 입니다. 생성자가 infix 연산자로 올때는 : 로 시작해야 합니다. deriving Show 는 좀 디버깅 쉬우라고, 화면에 출력하기 위해 사용했습니다.

몇 가지 헬퍼 함수를 만들면,

root :: Rose a -> a
root (x :> xs) = x

children :: Rose a -> [Rose a]
children (x :> xs) = r

size :: Rose a -> Int
size (x :> xs) = 1 + sum (map size xs)

leaves :: Rose a -> Int
leaves (_ :> []) = 1
leaves (_ :> xs) = 1 + sum (map leaves xs)

샘플 로즈 트리를 만들어 봅시다.

tree = 'x' :> map (flip (:>) []) ['a'..'z']

-- same as
tree = 'x' :> map (\c -> c :> []) ['a'..'z'] 

> tree
-- 'x' :> ['a' :> [],'b' :> [],'c' :> [],'d' :> [],'e' :> [],'f' :> [],'g' :> [],'h' :> [],'i' :> [],'j' :> [],'k' :> [],'l' :> [],'m' :> [],'n' :> [],'o' :> [],'p' :> [],'q' :> [],'r' :> [],'s' :> [],'t' :> [],'u' :> [],'v' :> [],'w' :> [],'x' :> [],'y' :> [],'z' :> []]

> size tree
-- 27

> leaves tree
-- 26

Functor

좀 삼삼하죠? 할게 별로 없으니. rose tree 를 functor 로 만들어 봅시다. 아래 짤방이 아마 세상에서 펑터를 가장 쉽게 설명할겁니다. fmap (+3) (Just 2) 에 대해

(http://adit.io)

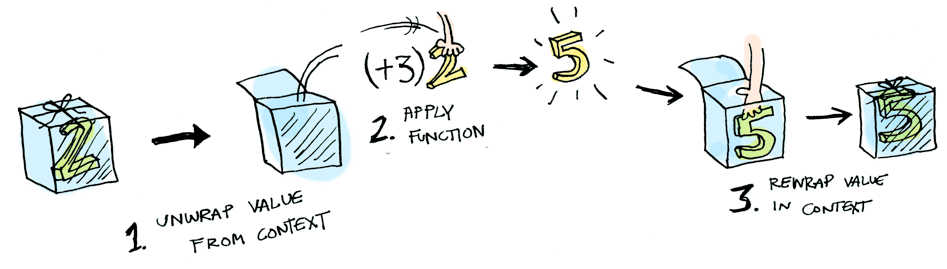
즉, Just 는 펑터이므로 2 를 꺼내 +3 을 적용하고, 다시 Just 를 씌워 Just 5로 만들어 줍니다. 그게 fmap 이 하는 일이고, 모든 functor 는 fmap 이 적용 가능합니다. functor 의 정의를 보면

class  Functor f  where
    fmap        :: (a -> b) -> f a -> f b

타입이 직관적이죠? a -> b 함수를 받아, f a 에 함수를 적용해서 f b 를 만듭니다. f 는 컨테이너라고 보시면 됩니다. Maybe 같은 것들요 대표적인 Functor 로

instance  Functor Maybe  where
    fmap f Nothing = Nothing
    fmap f (Just x) = Just (f x)
    

instance  Functor []  where
    fmap = map

그럼 우리가 만든 Rose 는 어떻게 해야 Functor 로 만들 수 있을까요?

instance Functor Rose  where
    fmap g (x :> xs) = g x :> map (fmap g) xs

직관적으로 보면 됩니다. 루트에 g 를 적용하고, xs 는 [Rose] 이므로 x :> xs 와 똑같이 취급해서 fmap g 를 적용하면 됩니다. 이 때 지켜줘야 하는 functor laws 는

fmap id  ==  id
fmap (f . g)  ==  fmap f . fmap g

그럼 이제, 좀 재미난걸 할 수 있습니다. 이젠 Rose 가 functor 니까요. 다양한 함수를 적용할 수 있죠.

tree' = 1 :> map (flip (:>) []) [1..5]

> tree'
-- 1 :> [1 :> [],2 :> [],3 :> [],4 :> [],5 :> []]

> fmap (+1) tree'
-- 2 :> [2 :> [],3 :> [],4 :> [],5 :> [],6 :> []]

> fmap (*10) tree'
-- 10 :> [10 :> [],20 :> [],30 :> [],40 :> [],50 :> []]

> fmap (:> []) tree'
-- (1 :> []) :> [(1 :> []) :> [],(2 :> []) :> [],(3 :> []) :> [],(4 :> []) :> [],(5 :> []) :> []]

Monoid

monoid 는 mempty, mappend 두개의 함수를 가지고 있는 m 타입의 인스턴스입니다.

mappend :: m -> m -> m 은 associative 한 연산자로, 두 m 을 받아서, 하나의 m 으로 합칩니다.
mempty :: m 은 mappend 의 neutral element 를 표현합니다.

뭔소리야 하실텐데, 우리 주변의 많은 것들이 monoid 입니다. 예제를 봅시다.

> (5 + 6) + 10 == 5 + (6 + 10)
True

> (5 * 6) * 10 == 5 * (6 * 10)
True

> ("Hello" ++ " ") ++ "world!" == "Hello" ++ (" " ++ "world!")
True

[Char] 에서 mempty 는 [] mappend 는 ++ 입니다. Integer 의 mappend 는 다양한데, + 라면 mempty 가 0 이고, * 라면 mempty 가 1 일 겁니다. 항등원 기억나시죠? 그거랑 비슷합니다.

class  Monoid a  where
    mappend :: a -> a -> a
    mempty  :: m
    mconcat :: [a] -> a
    mconcat :: foldr mappend mempty

mconcat 은 foldr (++) [] 를 생각하시면 이해가 쉽습니다. 네! 리스트도 모노이듭니다!

instance  Monoid [a]  where
    mempty = []
    mappend = (++)

모노이드를 일종의 연산과 그에 대한 항등원이 구현된 클래스라 보셔도 됩니다. 그러면 Sum, Product 모노이드를 만들어 보죠. Rose 에 적용할 수 있을 것 같아요.

newtype Sum a = Sum { getSum :: a } deriving Show
newtype Product a = Product a deriving Show

unProduct :: Product a -> a
unProduct (Product x) = x

instance Num a => Monoid (Sum a) where
  mempty = Sum 0
  Sum x `mappend` Sum y = Sum (x + y)
  
instance Num a => Monoid (Product a) where
  mempty = Product 1
  Product x `mappend` Product y = Product (x * y)

중간에 보면 unProduct 란게 있는데, 생성자에서 getSum 처럼 accessor 를 만들어 주면 필요 없고, 안만들어 주면 저렇게 만들어서 써야 합니다. 차이점을 보여드리기 위해 두 방법을 모두 사용 해봤어요. 근데, accessor 가 있으면 출력때 같이 나와서 좀 불편합니다.

-- 6 * (3 + 4)
> unProduct (Product 6 `mappend` (Product . getSum $ Sum 3 `mappend` Sum 4))

-- 42

무튼, 이제 모노이드도 있겠다, Rose 에 적용할 수 있습니다. 이게 무슨 뜻이냐면, Rose 컨테이너가 가진 value 가 Product, Sum 연산이 가능하게끔 바꿀 수 있다는 뜻입니다.

> tree'
-- 1 :> [1 :> [],2 :> [],3 :> [],4 :> [],5 :> []]

> fmap Sum tree'
-- Sum 1 :> [Sum 1 :> [],Sum 2 :> [],Sum 3 :> [],Sum 4 :> [],Sum 5 :> []]

> fmap Product tree'
-- Product 1 :> [Product 1 :> [],Product 2 :> [],Product 3 :> [],Product 4 :> [],Product 5 :> []]

Foldable

(https://www.haskell.org)

foldable 은 진짜 말 그대로 접을 수 있는 연산 fold 를 지원하는 인스턴스를 말합니다.

class Foldable t where
    fold    :: Monoid m => t m -> m
    foldMap :: Monoid m => (a -> m) -> t a -> m

    foldr   :: (a -> b -> b) -> b -> t a -> b
    foldr'  :: (a -> b -> b) -> b -> t a -> b

    foldl   :: (b -> a -> b) -> b -> t a -> b
    foldl'  :: (b -> a -> b) -> b -> t a -> b

    foldr1  :: (a -> a -> a) -> t a -> a
    foldl1  :: (a -> a -> a) -> t a -> a

여기선 fold, foldMap 만 다루도록 하죠. fold 의 타입을 보면 아시겠지만, Monoid m 의 컨테이너인 Foldable t 를 접어서 단일 m 으로 만듭니다.

따라서 복수개의 Sum, Product 를 접어 하나로 만들수 있지요. 어차피 이 두 모노이드에 대해 연산 자체는 정해져 있기 때문에 접는법만 알려주면 됩니다.

그리고 더 중요한 사실은, Rose 가 Foldable 이 되면 Sum 등이 적용된 Rose 를 접어 계산할 수 있습니다. 다시 말해 컨테이너에, 연산을 추가하고, fold 할 수 있다는 이야기지요.

아참! foldMap 은 이름에서 볼 수 있듯이 fmap 후 fold 한다고 생각하면 쉽습니다. fold . fmap 처럼요.

class Functor f => Foldable f where
  fold :: Monoid m    => f m -> m
  foldMap :: Monoid m => (a -> m) -> (f a -> m)
  foldMap = fold $ fmap g a
  
instance Foldable Rose where
  fold (x :> xs) = (h.g) xs `mappend` x
    where g = map (fold)
          h = foldr (mappend) mempty

직관적으로 보면 쉽습니다. h 는 모노이드 m 을 펼치는 역할을 합니다. g 는 f m 을 재귀적으로 펼치구요. 이는 로즈 트리가, 복수개의 자식 노드를 가질 수 있기 때문에 그런건데, 어찌 되었든 펼치면서 노드를 끝에다 붙여 나갑니다.

먼저 로즈 트리를 펼친 후에 모노이드를 합칠거니까, 순서는 (g.h) 입니다.

이제 그러면, 로즈트리가 functor 이므로 모노이드로 감쌀 수 있고 (연산을 지정할 수 있고) 게다가 foldable 이므로 그 연산을 이용해 하나로 접을 수 있습니다.

> tree'
-- 1 :> [1 :> [],2 :> [],3 :> [],4 :> [],5 :> []]

> fmap Sum tree'
-- Sum 1 :> [Sum 1 :> [],Sum 2 :> [],Sum 3 :> [],Sum 4 :> [],Sum 5 :> []]

> fold $ fmap Sum tree'
-- Sum 16

> unSum $ fold $ fmap Sum tree'
-- 16

~~갓스켈~~

References

(1) DelftX FP 101x
(2) Programming in Haskell
(3) Functor, Monad, Applicative
(4) Haskell WikiBooks - Monoids
(5) Foldable, Traversable
(6) foldable and traversable