하스켈로 배우는 함수형 언어 4
이번시간엔 모나드를 배웁니다. 네. 올것이 왔습니다. 간단한 파서를 구현하는 것 부터 시작해 보겠습니다.
What is a Parser
Parser (파서) 란 텍스트 조각을 분석하여 syntaxtic structure 를 만들어 내는 프로그램(코드)를 말합니다.
많은 프로그램들이 자신만의 파서를 가지고 있습니다. GHC 는 haskell , UNIX 는 shell script, explorer 는 HTML 분석합니다.
The Parser Type
type Parser = String -> Tree
하스켈 같은 함수형 언어에서 파서는 함수라 볼 수 있습니다. 문자열을 받아서 Tree (트리) 를 만들어 주는 함수처럼요.
때때로 입력된 문자열이 이상하다면 파서가 제대로 동작하지 않을수도 있습니다. 그럴때 분석되지 않은 문자열을 돌려주려면 이런 형태여야 합니다.
type Parser = String -> (Tree, String)
어떤 문자열들은 여러가지로 해석될 수도 있겠지요. 그럼 리스트를 돌려줘야겠네요.
type Parser = String -> [(Tree, String)]
꼭 파서가 트리를 만들 필요는 없지 않을까요? 문자열이 1 + 2 라면 이 값을 더한 3 을 돌려줄 수도 있을겁니다.
type Parser a = String -> [(a, String)]
이번 강의에서는 복잡한 파서를 구현하기 보다 파서가 무슨일을 하는지에 집중할 것이므로 파서의 타입을 심플하게 가져가겠습니다. 파서가 문자열을 분석하는데 실패하면 [] 성공하면 singleton list 를 돌려주겠습니다.
Basic Parsers
먼저 문자열에서 첫 번째 원소를 소비하고, 나머지를 돌려주는 간단한 item 파서를 만들어 봅시다. 이 파서는 빈 문자열에 대해서는 [] 를 돌려줍니다.
module Lecture7 where
type Parser a = String -> [(a, String)]
item :: Parser Char
item = \xs -> case xs of
[] -> []
(x:xs) -> [(x, xs)]
실행하면 이런 결과를 얻습니다.
> item "hello world"
-- [('h',"ello world")]
> item ""
-- []
항상 [] 만 돌려주는 failure 파서와 a -> Parser a 타입의 return 도 만들어 봅시다. 하나는 항상 실패하고, 다른 하나는 항상 성공하는 파서입니다.
failure :: Parser a
failure = \xs -> []
return :: a -> Parser a
return v = \xs -> [(v, xs)]
> failure "hello world!"
-- []
> (return "hello") " world"
-- [("hello"," world")]
> (return "hello") ""
-- [("hello","")]
이제 두 개의 파서를 붙이는 함수 (+++) 를 만들어 봅시다. p +++ q 에 대해 파서 p 가 성공하면 p 의 리턴값을, p 가 실패하면 q 가 처리하게 합시다. 위에서 항상 성공하는 파서 return v 와 항상 실패하는 파서 failure 를 여기다 붙이며 어떻게 될지도 한번 생각해 보는것도 좋습니다.
(+++) :: Parser a -> Parser a -> Parser a
p +++ q = \xs -> case p xs of
[] -> parse q xs
[(y, ys)] -> [(y, ys)]
parse :: Parser a -> String -> [(a, String)]
parse p xs = p xs
여기서 parse 는 그냥 readable 한 코드를 만들기 위해 사용했다고 보면 됩니다. 파서와 텍스트를 받아서 그 적용한 결과를 돌려줍니다.
> parse (return '1') "234"
-- [('1',"234")]
> parse failure "abcd"
-- []
> parse (failure +++ (return '1')) "abcd"
-- [('1',"abcd")]
> parse (item +++ return 'd') "abc"
-- [('a', "bc")]
Monad
여기서 잠깐 생각해 볼 거리가 있습니다. “parser 가 대체 무슨일을 하고 있는가?”
파서의 타입을 잘 보면 원본 타입 String 을 받아, 여기서 부가적인 작업을 해서 a 타입을 만들고, 다시 본래 타입인 String 더해 튜플로 만들어 돌려줍니다. 다시 말해 파서는 한 타입을 받아 부가적인 정보를 만들어 본래 타입에 붙여주는 함수 라 볼 수 있습니다.
파서의 연결을 도와주는 함수는 (+++) 무엇일까요? *부가적인 정보를 붙여주는 파서 를 합성* 해 주는 역할을 합니다.
지금 (+++) 의 규칙은 p 가 실패하면 q 를 적용하지만, 파서 t, u, v 를 받아 모두 적용한 뒤 결과를 돌려주는 연산자도 만들 수 있습니다.
(+++) 자체는 하나의 규칙을 의미하지만 자세히 보면 이외에도 다양한 규칙을 가진 합성 함수를 만들 수 있다는 것을 알 수 있습니다.
부가적인 정보를 만들어 내는 함수와(파서), 이 파서간의 합성이 아주 중요한 키 포인트입니다. 그리고 이 파서가 바로 monad 입니다. 두둥
The parser type is a monad, a mathematical structure that has proved useful for modeling many different kinds of computations
Sequencing
위에서는 두개의 파서를 엮어 하나로 만들긴 했지만 둘 중에 하나만 사용했죠. 둘 다 사용하진 않았습니다. 그럼 둘 이상의 파서를 엮어 하나의 파서를 만들려면 어떻게 해야할까요? 일단 생각해 볼 수 있는건 타입이 좀 다릅니다.
서로 다른 두개의 파서 Parser a 와 Parser b 를 고려해 봅시다.
type Parser a = String -> [(a, String)]
Parser a
-- String -> [(a, String)]
Parser b
-- String -> [(b, String)]
Parser a 의 출력은 [(a, String)], 이기 때문에 다른 파서 Parser b 의 입력 String 이 될 수 없습니다.
그리고 여기서 한 가지 더 중요한 사실은, Parser a 가 String 을 이용해 만든 타입 a 의 부가정보를 Parser b 에 손실 없이 넘겨줘야 한다는 사실입니다. 그래야만 파서를 조합한 의미가 있지요.
정리하자면 Parser a 를 받아 Parser b 를 돌려주는 파서 조합함수 를 만들 것인데, 부가정보 a 의 보존을 위해 이 함수 내부에서 a -> Parser b 타입의 중간 함수가 필요합니다. 이 중간 함수가 어디에서 어떤 일을 할지가 구현해야 할 부분이자, 가장 중요한 부분입니다. 파서 종류에 따라 원본 데이터 (여기서는 String) 을 조작하는 방법이 다르기 때문입니다. 거꾸로 말하면 다양한 종류의 파서가 있다는 말 입니다.
함수의 이름은 >>= 라 짓겠습니다. bind 라 읽습니다. 타입은
type Parser a = String -> [(a, String)]
parse :: Parser a -> String -> [(a, String)]
parse p xs = p xs
(>>=) :: Parser a -> (a -> Parser b) -> Parser b
구현은
p >>= q = \xs -> case p xs of
[] -> []
(y, ys) -> parse (q y) ys
즉 >>= 는 Parser a 의 처리 결과가 [] 이면 [] 을 돌려줍니다. 올바르게 처리되었을 경우에는 Parser a 의 결과로 얻어진 부가정보 a 타입에 대해 a -> Parser b 타입의 함수인 y 에게 넘겨 Parser b 를 받고 결과적으로는 \xs -> parse k ys 를 돌려줍니다. (k :: parser b) 그런데, 여기서 parse k ys 의 결과가 [(b, String)] 이기 때문에 \xs -> parse k ys 는 Parser b 라 볼 수 있습니다.
최종적으로는 Parser a 를 이용해 Parser b 를 만들어 냈습니다.
예제를 한번 보시죠. Parser Char 을 이용해 Parser (Char, Char) 을 만들어 볼 수 있습니다.
return :: a -> Parser a
return v = \xs -> [(v, xs)]
(>>=) :: Parser a -> (a -> Parser b) -> Parser b
p >>= q = \xs -> case p xs of
[] -> []
(y, ys) -> parse (q, y) ys
-- consume only one Char
parseTwice :: Parser (Char, Char)
parseTwice = item >>= \x -> return (x, x)
parseTwice "5BEAF"
-- [((5, 5), "BEAF")]
item 과 return (x, x) 두개의 파서를 조합해서 parseTwice 라는 새로운 파서를 만들었습니다. 조금 더 붙여볼까요?
ignore2 :: Parser (Char, Char)
ignore2 = item >>= \x -> item >>= \y -> item >>= \z -> return (x, z)
> ignore2 "2A371"
-- [(('2','3'),"71")]
Do
위에서 보았듯이 같은 원본 타입 String 을 가지는 같은 종류의 파서(모나드)는 계속 연결할 수 있습니다. p1, ..., pn 을 파서라 하고 v1, ..., vn 을 파서가 만드는 부가정보라 할 때 다음과 같이 일반화 할 수 있습니다.
p1 >>= \v1 ->
p2 >>= \v2 ->
p3 >>= \v3 ->
...
pn >>= \vn ->
return (f v1 v2 ... vn)
하스켈에선 조금 더 편한 문법을 지원하는데요 바로 do 구문입니다.
do v1 <- p1
v2 <- p2
...
vn <- pn
return (f v1 v2 ... vn)
Monadic Axioms
이 때 do 구문을 활용하는 파서(모나드) pn 에 대해서는 미리 >>= 과 return 이 구현되어 있어야 합니다. 우리도 위에서 두 가지 함수를 사용했습니다.
하스켈에서는 모나드 클래스가 따로 있습니다. 그리고 모든 모나드 클래스의 인스턴스는 최소한 >>= 와 return 을 구현해야 합니다. 우리가 위에서 구현했던 파서를 잠깐 보면
type Parser a = String -> [(a, String)]
return :: a -> Parser a
return v = \xs -> [(v, xs)]
(>>=) :: Parser a -> (a -> Parser b) -> Parser b
p >>= q = \xs -> case parse p xs of
[] -> []
[(y, ys)] -> parse (q y) ys
return 은 a 를 받아 파서를 돌려줍니다. >>= 는 파서(모나드)를 결합하지요.
아까 다양한 파서(모나드)가 있을 수 있다고 말했던 것 기억 나시죠? 많은 종류의 모나드에 대해 최소한 return 과 >>= 를 구현해야 하는데, 이때 지켜져야 할 axioms (공리) 가 있습니다.
(1) m >>= return == m (right unit)
(2) return x >>= f == f x (left unit)
(3) (m >>= f) >>= g == m >>= (\x -> f x >>= g) (associativity)
So, Why Monad?
근데, 이런 복잡한 모나드가 왜 중요한걸까요? 바로 부가정보 를 만들면서 본래의 타입을 유지하기 때문입니다.
본래 순수 함수형 프로그래밍에선 콘솔 출력 같은 side-effect 를 만들 수 없습니다. 그러나 모나드를 이용하면 부가정보 (= side-effect) 와 연산 부분 (purely functional) 를 분리할 수 있습니다.
실제 하스켈에서도 IO Monad 를 통해 입출력을 할 수 있죠.
Monad, Again
그러면 실제로 하스켈에서 제공하는 모나드를 클래스를 사용해 봅시다. 코드를 조금 변경해야합니다.
module Lecture7 where
import Control.Monad
-- ref: http://www.cs.nott.ac.uk/~gmh/Parsing.lhs
newtype Parser a = P (String -> [(a, String)])
instance Monad Parser where
return v = P $ \inp -> [(v, inp)]
p >>= f = P $ \inp -> case parse p inp of
[] -> []
[(v, out)] -> parse (f v) out
item :: Parser Char
item = P $ \inp -> case inp of
[] -> []
(x:xs) -> [(x, xs)]
parse :: Parser a -> String -> [(a,String)]
parse (P p) inp = p inp
ignore2 :: Parser (Char, Char)
ignore2 = do x <- item
item
z <- item
return (x, z)
실제 돌려보면,
> parse ignore2 "7A3BCEF"
-- [(('7','3'),"BCEF")]
MonadPlus
아까 작성했었던 파서 failure, (+++) 기억 나시나요? failure 는 항상 실패하는 파서를, (+++) 는 첫번째 파서와 두번째 파서를 붙여 둘 중 성공하는 하나의 파서만 선택하는 합성 파서입니다.
하스켈에선 이런 두 가지 특징을 구현한 모나드를 MonadPlus 라 부릅니다. 다시 말해 MonadPlus 에는 기본적인 return 이나 >>= 이외에도 위 두 가지가 더 구현되어 있다는 말이죠.
MonadPlus 에서는 failure 대신 mzero 를 (+++) 대신 mplus 란 이름을 사용합니다.
instance MonadPlus Parser where
mzero = P $ \_ -> []
p `mplus` q = P $ \inp -> case parse p inp of
[] -> parse q inp
[(v, out)] -> [(v, out)]
failure :: Parser Char
failure = mzero
(+++) :: Parser a -> Parser a -> Parser a
p +++ q = p `mplus` q
> parse (item +++ return 'd') "abc"
-- [('a',"bc")]
> parse (item +++ return 'd') ""
-- [('d',"")]
Derived Primitives
이제 파서를 엮어서 다양한 파서를 만들어 봅시다.
import Data.Char
sat :: (Char -> Bool) -> Parser Char
sat p = do x <- item
if p x then return x else failure
digit :: Parser Char
digit = sat isDigit
lower :: Parser Char
lower = sat isLower
upper :: Parser Char
upper = sat isUpper
letter :: Parser Char
letter = sat isAlpha
alphanum :: Parser Char
alphanum = sat isAlphaNum
char :: Char -> Parser Char
char x = sat (== x)
여기서 char 을 이용하면 지정된 문자열이 있는지 검사하는 파서 string 을 만들 수 있습니다.
string :: String -> Parser String
string [] = return []
string (x:xs) = do char x
string xs
return (x:xs)
string 은 재귀를 이용해 작성했는데, 입력된 문자열이 모두 존재할 경우에만 return 하고 아니면 [] 를 돌려줍니다. (do 매크로는 중간에 [] 가 나오면 [] 를 바로 리턴합니다.)
> parse (string "google") "naver google yahoo"
-- []
> parse (string "google") "google yahoo"
-- [("google"," yahoo")]
> parse (string "google") "goo yahoo"
-- []
그러면, digit 나 letter 같은 파서에 대해 동일한 파서를 여러번 사용하려면 어떻게 해야 할까요? string 처럼 재귀를 이용해 매번 파서를 만들어야 할까요?
그렇지 않습니다. mutual recursion 을 이용해서 파서를 받아 여러번 적용해 주는 many 란 파서를 만들어 봅시다.
many :: Parser a -> Parser [a]
many p = many1 +++ return []
many1 :: parser a -> Parser [a]
many1 p = do x <- p
xs <- many p
return (x:xs)
many 는 p 을 0번 이상, many1 은 적어도 1번 이상 p 를 적용합니다.
many 를 활용하면 변수의 이름도 파싱할 수 있습니다. 변수의 이름은 첫 글자가 소문자로, 나머지는 알파벳 혹은 숫자로 구성되어 있다고 하면 이를 위한 파서 ident 는
ident :: Parser String
ident = do x <- lower
xs <- many alphanum
return (x:xs)
> parse ident "left = 3"
-- [("left"," = 3")]
이제 뭔가 파서가 좀 쓸만해 보이죠? 자연수를 파싱하는 nat 와 스페이스를 파싱하는 space 를 만들어 보겠습니다.
nat :: Parser Int
nat = do xs <- many1 digit
return (read xs)
space :: Parser ()
space = do many (sat isSpace)
return ()
> parse nat "123 abc"
-- [(123," abc")]
> parse space " abc"
-- [((),"abc")]
코드를 분석하는 파서를 만들때 스페이스를 주의해야 합니다. 예를 들어 1+2 와 1 + 2 는 같은 코드입니다.
파서를 받아 앞 뒤로 붙은 스페이스를 제거하는 기능을 덧붙인 파서를 돌려주는 token 이란 함수를 만들어 봅시다. 그리고 나면 token 을 활용해 identifier, natural, symbol 을 만들겁니다.
token :: Parser a -> Parser a
token p = do space
v <- p
space
return v
identifier :: Parser String
identifier = token ident
natural :: Parser Int
natural = token nat
symbol :: String -> Parser String
symbol xs = token (string xs)
이제 이걸 엮어서 숫자 리스트를 분석하는 파서를 만들어 봅시다.
nlist :: Parser [Int]
nlist = do symbol "["
n <- natural
ns <- many (do symbol ","
natural)
symbol "]"
return (n:ns)
> parse nlist "[1, 2, 3]"
-- [([1,2,3],"")]
> parse nlist "[1, 2]"
-- [([1,2],"")]
> parse nlist "[1, 2"
-- []
> parse nlist "[1 2"
-- []
> parse nlist "[1,"
-- []
모나드의 세계란 참으로 놀랍죠?
Arithmetic Expressions
이제 단순한 텍스트가 아니라, 코드를 분석해 보죠. 우선 작은 수식을 분석하는 파서를 작성해 봅시다. 우리가 작성할 파서는 정수에 대한 * 과 + 만 처리할 수 있습니다. 간단히 문법을 만들어 보면
expr ::= expr + expr | term
term ::= term * term | factor
factor ::= (expr) | nat
nat ::= 0 | 1 | 2 | ...
처음보면 난해할 수 있습니다. 이 그림과 비교해가며 보세요. 완벽히 일치하진 않지만 대략적인 설명을 해줍니다.
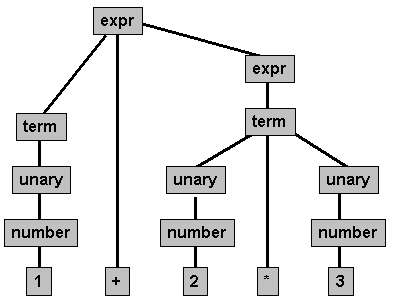
그런데, 실제로 2 + 3 + 4 에 적용해보면, (2 + 3) + 4 과 2 + (3 + 4) 두 가지 방법으로 해석될 수 있습니다. 따라서 모호함을 제거하기 위해
expr ::= term + expr | term
term ::= factor * term | factor
factor ::= (expr) | nat
nat ::= 0 | 1 | 2 | ...
이제 2 + 3 + 4 는 확실히 2 + (3 + 4) 입니다. 괴상한 문법을 하스켈로 옮기기 위해 조금 더 다듬어 보도록 하지요.
term + expr | term 은 사실 term + (expr | e) 과 동일합니다. (e 는 비었음 을 의미) factor * term | factor 도 factor + (term | e) 구요. 따라서
expr ::= term + (expr | e)
term ::= factor + (term | e)
factor ::= (expr) | nat
nat ::= 0 | 1 | 2 | ...
이제 하스켈 코드로 옮길겁니다. 우리는 트리를 만드는 대신 바로바로 계산할 겁니다.
expr :: Parser Int
expr = do t <- term
do symbol "+"
e <- expr
return (t + e)
+++ return t
term :: Parser Int
term = do f <- factor
do symbol "*"
t <- term
return (t * f)
+++ return f
factor :: Parser Int
factor = do symbol "("
e <- expr
symbol ")"
return e
+++ natural
return t 도 하나의 파서고, +++ 로 둘 중 올바르게 작동하는 파서만 택함으로써 문법에서의 | 를 구현했습니다.
이제 파싱된 결과를 해석하는 eval 함수를 만들어 봅시다.
eval :: String -> Int
eval xs = case parse expr xs of
[(n, [])] -> n
[(_, out)] -> error ("ununsed input: " ++ out)
[] -> error ("invalid input: " ++ xs)
> eval "2 * 3 + 4"
-- 10
> eval "2 * (3 + 4)"
-- 14
> eval "2 * 3 +"
-- *** Exception: ununsed input: +
> eval "2 * 3 - 4"
-- *** Exception: ununsed input: - 4
> eval "-4"
-- *** Exception: invalid input: -4
Programming With Effects
Programming With Effects 는 Programming in Haskell 의 저자인 Graham Hutton 이 작성한 글입니다. 모나드에 대해 이보다 쉽고, 간결하게 설명한 글은 찾기 힘들죠.
Programming with Effects 를 참고하여 몇 가지 예제를 더 작성해 보면서 모나드에 더 익숙해져 봅시다.
data Expr = Val Int | Div Expr Expr
위와 같은 Expr 이 있다고 합시다. 평가하기 위해서 eval 함수를 만들고 실행해 봅시다.
eval :: Expr -> Int
eval (Val n) = n
eval (Div x y) = eval x `div` eval y
> eval (Val 3)
-- 3
> eval (Div (Val 3) (Val 4))
-- 0
> eval (Div (Val 8) (Val 4))
-- 2
> eval (Div (Val 8) (Val 0))
-- *** Exception: divide by zero
0 으로 나누니 에러가 발생합니다. expr 이 Val 0 인지 아닌지를 판별할 필요가 있습니다.
조금 더 고쳐보면
import Prelude hiding (Maybe, Just, Nothing)
data Expr = Val Int | Div Expr Expr
data Maybe a = Nothing | Just a
safediv :: Int -> Int -> Maybe Int
safediv n m = if m == 0 then Nothing else Just (n `div` m)
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div x y) = case eval x of
Nothing -> Nothing
Just n -> case eval y of
Nothing -> Nothing
Just m -> safediv n m
너무 복잡합니다. eval 에서 safediv 에 인자를 넘기는 부분을 추상화하면
seqn :: Maybe a -> Maybe b -> Maybe (a, b)
seqn _ Nothing = Nothing
seqn Nothing _ = Nothing
seqn (Just x) (Just y) = Just (x, y)
apply :: (a -> Maybe b) -> Maybe a -> Maybe b
apply f Nothing = Nothing
apply f (Just x) = f x
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div x y) = apply f (eval x `seqn` eval y)
where f (n, m) = safediv n m
조금 더 간편해졌습니다. 그런데 만약 인자가 3개인 연산자에 대해 평가 방법을 정의한다면
eval (Op x y z) =
apply f (eval x `seqn` (eval y `seqn` eval z))
where f (a, (b, c)) =
괄호가 점점 중첩됩니다. 모든 것을 나중에 seqn 로 모든 결과를 모아 f 에서 처리하기 보다는 Maybe a 를 받아 a -> Maybe b 를 바로 적용해 Maybe b 를 돌려주고, 이런식으로 순차적으로 처리하는 방식으로 바꿔봅시다.
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
m >>= f = case m of
Nothing -> Nothing
Just x -> f x
eval :: Expr -> Maybe Int
eval (Val x) = Just x
eval (Div x y) = eval x >>= \n ->
eval y >>= \m ->
safediv n m
어디서 많이 보다싶은 식이죠? 바로 하스켈의 do 와 비슷합니다.
하스켈에서 Eq 의 클래스의 정의는 이렇게 되어있습니다.
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x /= y = not (x == y)
이 말은 Eq 클래스의 인스턴스가 되는 a 타입은 무조건 == 를 구현해야 한다는 뜻입니다. (/= 는 이미 구현되어 있는거 보이시죠?)
마찬가지로 타입 m 으로 parameterized 된 Monad 클래스의 인스턴스 또한 다음의 두 함수를 구현해야 합니다.
class Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
예를 들어 Maybe 같은 경우
instance Monad Maybe where
return x = Just x
Nothing >>= _ = Nothing
(Just x) >>= f = f x
List Monad
Maybe 모나드를 잘 보면 Nothing 은 실패를, Just x 는 성공을 나타내는 연산으로 볼 수 있습니다.
리스트 모나드는 이런 개념을 좀 더 일반화한 것입니다. 복수번의 성공이 있을 수 있죠.
instance Monad [] where
return x = [x]
xs >>= f = concat (map f xs)
이를 이용하면 pairs 와 같은 함수를 만들수 있습니다.
pairs :: [a] -> [b] -> [(a, b])
pairs xs ys = do x <- xs
y <- ys
return (x, y)
> pairs [1, 2, 3] [4, 5, 6]
-- [(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6)]
list comprehension 구문과 비슷합니다. 실제로 do 와 list comprehension 모두 리스트의 >>= 를 이용합니다.
State Monad
한 상태(State) 에서 다른 상태로 변환시켜주는 state transformer 의 타입은 이렇게 정의할 수 있을 겁니다.
type ST = State -> State
그리고 상태가 변하면서 어떤 정보를 남겼을때의 타입을 이렇게 만들어 볼 수 있겠죠.
type ST a = State -> (a, State)
어디서 많이 본것 같죠? 맞습니다. 위에서 본 Parser 입니다. String -> (a, String) 이였으니까, State 가 String 이었던 거죠.
instance Monad ST where
return x = \s -> (x, s)
st >>= f = \s -> let (x, s') = st s
in f x s'
누차 언급했듯이 >>= 는 모나드(연산)간 연결입니다. st 에 s 를 넣은 결과를 (x, s') 라 하면 다시 f x 에 s 를 넣어 연결할 수 있다는 뜻이지요.
위에서는 type 을 사용했지만 실제로 이 키워드를 사용하면 클래스의 인스턴스가 될 수 없습니다. ST 를 monadic type 클래스의 인스턴스로 만들려면 data 나 newtype 을 이용할 수 있습니다. data 의 경우엔 dummy constructor 가 필요합니다. 여기선 S 가 되겠습니다. dummy constructor 의 런타임 오버헤드를 피하려면 newtype 을 이용하면 됩니다.
그리고 이 예제에서는 dummy constructor 를 제거하기 위해 apply 함수를 만들어서 이용하겠습니다.
State 는 정수로 표시할겁니다.
type State = Int
data ST a = S (State -> (a, State))
apply :: ST a -> State -> (a, State)
apply (S f) x = f x
instance Monad ST where
return x = S (\s -> (x, s))
st >>= f = S (\s -> let (x, s') = apply st s in apply (f x) s')
이제 예제에서 활용할 간단한 이진트리를 정의해 봅시다. 이진트리의 leaf 는 a 타입의 값을 가지고 있습니다.
data Tree = Leaf a | Node (Tree a) (Tree b)
-- example
tree :: Tree Char
tree = Node (Node (Leaf 'a') (Leaf 'b')) (Leaf 'c')
이제 State 를 받아 +1 을 더한 다음 State 를 돌려주는 fresh 를 만들어 봅시다.
-- data ST a = S (State -> (a, State))
fresh :: ST Int
fresh = S (\n -> (n, n + 1))
즉 fresh 는 State 를 1 만큼 증가시키고 부가정보로 current state n 을 남깁니다. fresh 를 이용하면 위에서 만든 이진트리를 순회하면서 번호를 붙일 수 있습니다. 부가정보로 남는 n 을 Leaf 에다가 붙이는 것이죠.
다음 fresh 의 입력은 이전 fresh 의 아웃풋인 n + 1 이기 때문에 서로 다른 두 노드가 같은 숫자를 가질 일은 없습니다.
mlabel :: Tree a -> ST (Tree (a, Int))
mlabel (Leaf x) = do n <- fresh
return (Leaf (x, n))
mlabel (Node l r) = do l' <- mlabel l
r' <- mlabel r
return (Node l' r')
label :: Tree a -> Tree (a,Int)
label t = fst (apply (mlabel t) 0)
> label tree
-- Node (Node (Leaf ('a',0)) (Leaf ('b',1))) (Leaf ('c',2))
IO Monad
하스켈에서 입출력은 IO 모나드를 이용합니다. 무슨말인고 하니, 다음과 같은 axioms 를 구현한 IO 모나드 에 대해
return :: a -> IO a
(>>=) :: IO a -> (a -> IO b) -> IO b
getChar :: IO Char
putChar :: Char -> IO ()
다음처럼 do 구문을 이용해서 프로그램을 작성할 수 있다는 뜻입니다.
getLine :: IO String
getLine = do x <- getChar
if x == '\n' then
return []
else
do xs <- getLine
return (x:xs)
IO 모나드는 State 모나드 라 볼 수 있습니다. IO a 는 타입 a 의 부가정보를 만들면서 State 를 변화시키는 것으로요
type World = ...
type IO a = World -> (a, World)
여기서 입/출력이 수행되는 것은 action 에 의해 World 가 변경되는 것이라 볼 수 있습니다.
Derived Primitives
다양한 종류의 모나드에 대해 적용할 수 있는 함수를 만들 수 있습니다.
liftM 는 모나드에 대한 map 을 join 은 concat 을, >> 는 첫 번째 결과값을 다 버리고 두번째만 취하는 함수입니다. 마지막으로 sequence 는 모나드 익스프레션 리스트를 하나의 모나드 익스프레션으로 바꾸고, 그 결과를 리스트로 돌려줍니다. 타입을 보시면 이해가 빠를겁니다.
liftM :: Monad m => (a -> b) -> m a -> m b
liftM f mx = do x <- mx
return (f x)
join :: Monad m => m (m a) -> m a
join mmx = do mx <- mmx
x <- mx
return x
(>>) :: Monad m => m a -> m b -> m b
mx >> my = do _ <- mx
y <- my
return y
sequence :: Monad m => [m a] -> m [a]
sequence (mx:mxs) = do x <- mx
xs <- sequence mxs
return (x:xs)
References
(1) DelftX FP 101x
(2) error in sat function in “Programming in Haskell”
(3) http://wiki.reeseo.net/Haskell
(4) Understanding Monads
(5) http://www.csee.umbc.edu
(6) Programming With Effects by Graham Hutton
comments powered by Disqus