Process Mining 3: Metric, C-nets
Four Quality Criteria For Process Discovery
real process 로 부터 event log 를 얻고 이것으로 process model 을 만든다.
process model 을 평가하기 위해 해야하는 질문은
Is the process model a correct reflection of the real process?
그러나 real process 를 모르기 때문에 판단하기가 쉽지 않다. 일반적으로 데이터마이닝에서 사용하는 평가 지표인 confusion matrix 를 도입하면

- True Positive: traces possible in model and also possible in real process
- True Negative: traces not possible in model and also not possible in real process
- False Positive: traces possible in model and but not possible in real process
- False Negative: traces not possible in model and but possible in real process
보통은 평가 지표로 recall, precision, F1 score 등을 이용하는데 프로세스마이닝에서의 문제는 real process 에서 일어나는 FN, TP 를 알 수가 없다는 것이다.
따라서 event log 의 FN’, TP’ 를 이용해서 replay fitness 를 이용한다.
이 외에도 다양한 문제를 마주칠 수 있는데,
- 보통 이벤트로그로 부터는 FN’ 이 무엇인지 알 수 없다.
- 로그가 possible traces 의 일부분만 담고 있다.
- Almost vs poorly fitting traces
- 루프가 있으면 무한히 많은 possible traces 가 있다.
- Murphy’s law for process mining: Anything is possible, so pobabilities matter
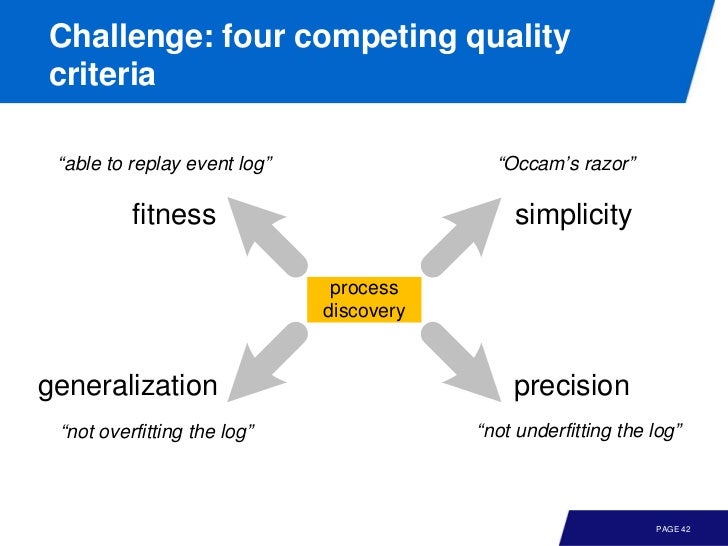
이런 문제점들은 다음의 기준들 사이에서 균형을 맞춰야 함을 알려준다.
- fitness: observed behavior fits
- simplicity: Occam’s razor
- precision: avoiding underfitting
- generalization: avoiding overfitting
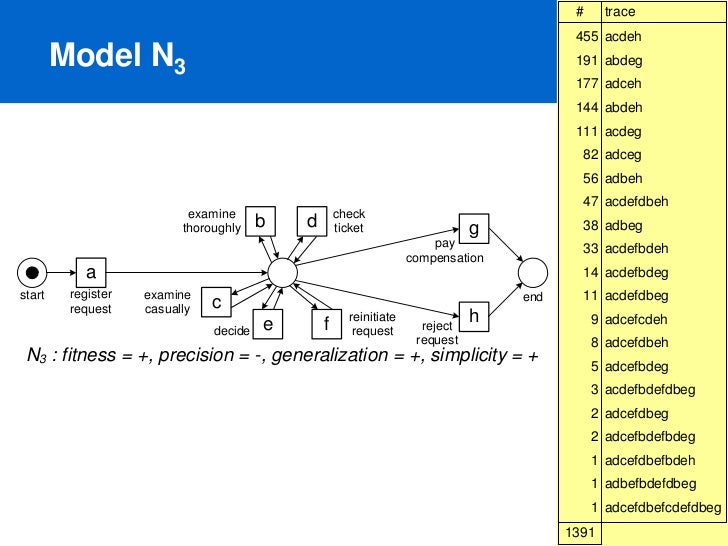
여기서 precision 이 문제가 되는 경우라는 것은, flower model 처럼 필요 이상으로 가능한 모든 경우의 수를 도입한 모델이라 보면 된다. 다시 말해서 기존의 log 와는 완전히 다른 로그가 모델에 맞을 경우를 말한다. (underfitting)
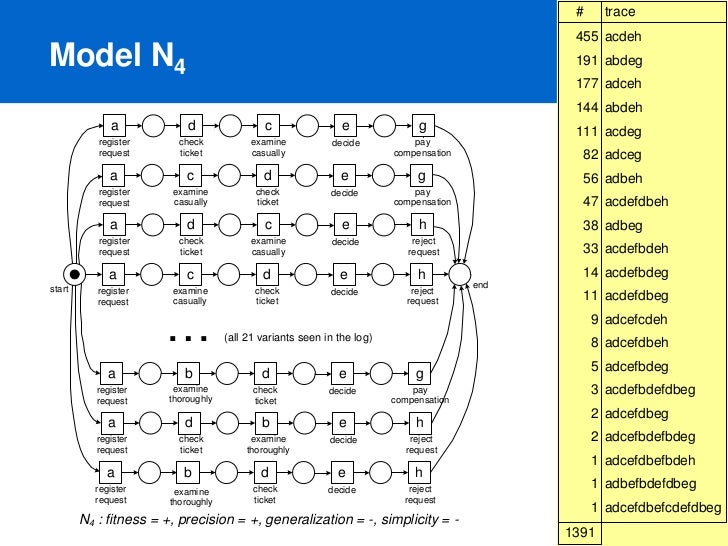
반대로 generalization 이 낮은 모델은, 너무 log 에 맞추느라 복잡해진 경우를 말한다. (overfitting)
따라서 traces 의 수가 적은 경우에 너무 overfitting 하려고 하면 퍼포먼스가 낮아진다. 반대로 traces 수가 상당히 많다면, 다음에 들어올 traces 가 다른 형태일 확률이 낮아지므로 모델을 조금 더 fitting 하는 편이 낫다. (오히려 이 경우는 overfitting 이라 보기 어렵다.)
Representational Bias
Modeling language provides a bias
예를 들어 petri net 같은 경우는 concurrency 를 모델링하는데 문제가 없는 반면 transition system 은 어렵다.
concurrency 에 대해서도 생각해 볼 것이, k = 10 의 parallel activities 가 있다면 가능한 traces 는 10! ~= 3600000 이다.
반면 알파 알고리즘이 이 모델을 발견하려면 단지 k(k-1 의 direct succession 만 필요하다.
그러나 알파 알고리즘은 optional(skip) 이 있는 모델을 발견하지 못한다. 그리고, silent transition(OR-joins) 이 있는 모델에서의 가능한 traces 수는
WF-net 같은 경우는 unique label 과 관련해서 문제가 있다.
L = [<a, c, d>^45, <b, c, e>^42, <a, c, e>^20]
이 있을때, WF-net 은 e 두개인 모델을 발견할 것이다.
그리고 만약 no indirected dependencies 라면,
L = [<a, c, d>^45, <b, c, e>^42] 에서 올바른 모델을 찾아내지 못할것이다. (a, b 가 d, e 의 선택에 영향을 준다.)
Visualization of discovered model != representatoinal bias
What is process discovery so difficult?
- There are no negative examples
- Due to concurrency, loops, and choices the search space has a complex structure and the log typically contains only a fraction of all possible behaviors
- There is no clear relation between the size of a model and its behavior
특히 마지막 문제는, 일반적인 경우에선 작은 모델이 작은 로그를 만들어 내지만 프로세스 마이닝에선 작은 모델이라도 많은 로그를 만들 수 있다.
따라서 representational bias 를 잘 고려해서 모델을 선택해야 한다.
Business Process Model and Notation (BPMN)
Representational bias impacts search space

exclusive OR 은 둘 중 하나만 선택이고, parallel 은 모두로 분기한다. inclusive OR 은 하나 이상을 선택할 수 있다. 더 자세한 내용은 BPMN Gateway 를 참고하자.
보통 inclusive OR join 이 있으면 synchronization 이 된다. 그리고 앞쪽에 inclusive OR split 이 있고 뒤쪽에 and join 이 있으면 deadlock 이 있을 가능성이 높다.
일반적으로는 OR join, split 을 AND join split 을 결합해야 데드락이 없다.
참고로 BPMN 은 UML 이나 Event-Driven Process Chains, EPCs 와 비스무리하다. 아래는 BPMN 예제

보통은 Petri net 이나 process tree 로 작업하고 BPMN 으로 변환한다. BPMN 으로 바로 작업하는 경우는 흔하지 않다고 함.
Vicious Cycle Paradox
이부분은 당최 뭔 소린지 이해가.. 나중을 위해서 그림만 넣어놈.
Dependency Graphs

footprint 의 casuality 를 이용해서 dependency graph 를 만들 수 있다. place 가 없는 일종의 Petri Net 이라 볼 수 있다.
참고로 casuality 는
causality:
x -> y, iffx > yand noty > x
dependency graph 는 의존성은 잘 보여주지만 executable semantic 이 없다. 각 노드는 OR join, split 의 fuzzy 로 볼 수 있다.
- Fuzzy models can be viewed as dependency graphs
- No precise semantics
- Many ways to create dependency graphs often based on heuristics
Casual Nets
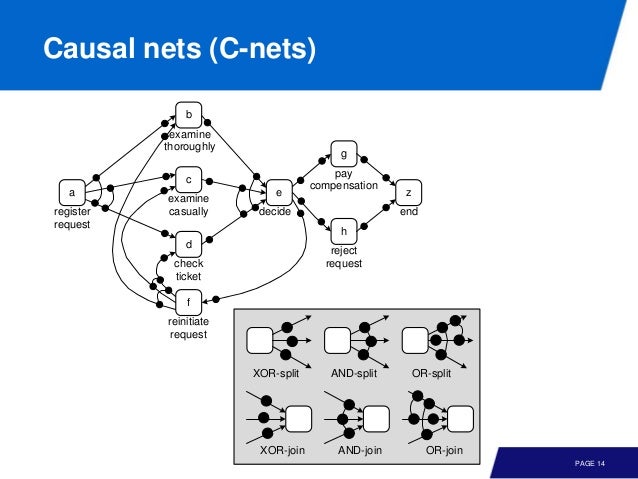
Casual nets, C-nets 은 dependency graph 에 inpt, output 을 붙여 possible behavior 를 보여준다.
왜 C-nets 을 이야기 할까?
- Output of several mining techniques, e.g., the well-known huritics miner
- Fits well with mainsteam languages (BPMN, EPCs, YAWL, etc.)
- Able to model XOR, AND, OR but no sidlent steps or duplicate activities needed
- Loose interpretation. focus on replay semantics rather then executing semantics
C-nets 에서는 obligation 이 token 의 역할을 한다.
Semantics are declarative
Only valid binding sequences are considered
C-nets 은 WF-nets 으로 쉽게 변환될 수 있다. WF-nets 에선 deadlock 이 있을 수 있는 반면 C-nets 에선 valid seq 만을 논하기 때문에 deadlock 은 이야기 하지 않는다.
Valid binding seqence of C-net is, Valid firing sequence of WF-net
그리고 C-net 이 WF-nets 보다 좀 더 표현적이다. 강의에서 나온 C-nets 같은 경우, 무한한 수의 b, c, d 를 표현하면서도 order 가 유지되고, b, c, d 가 같은 수로 반복된다.
Heuristic Mining
(1) Learn a dependency graph by counting freq => dependency graph
(2) Learn splits and joins => C-nets
(3) visualize (and convert if needed) => BPMN, etc.
Learning Dependency Graphs
알파 알고리즘을 이용하면 별별 문제가 다 생기는데, 휴리스틱하게 모델을 만들면 이런 문제는 좀 피할 수 있다.
그리고 한 가지 더 생각해 볼 문제는
Freqencies matter
무슨 말인고 하니, 빈번한 로그만 valid 취급하면 overfitting 을 피할 수 있다. 알파 알고리즘에 적용하면, 좀 빈도수가 많은 것들만 valid casuality 로 취급할 수 있다.

Dependency Measure

dependency measure 값은 -1 ~ 1 인데, 1 에 가까울 수록 casuality 가 있다. 아래 그림은 threshold 를 넘는 direct succession, casuality 만 표시한 dependency graph 다.
threshold 가 높아질 수록 그래프가 심플해진다.
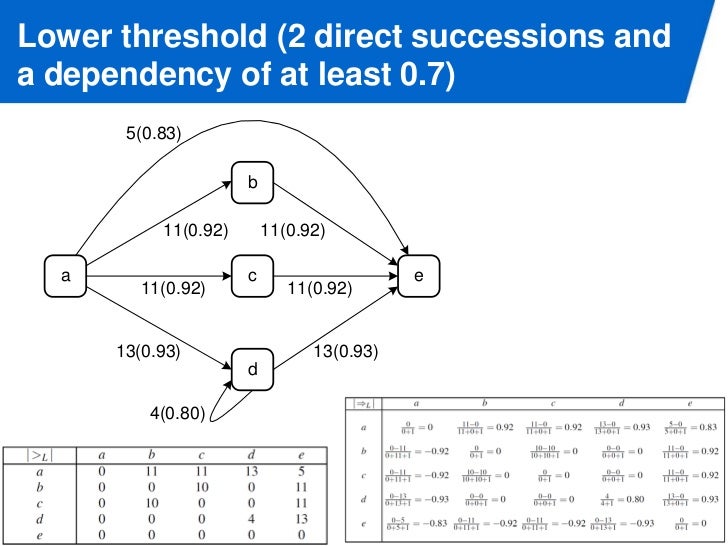
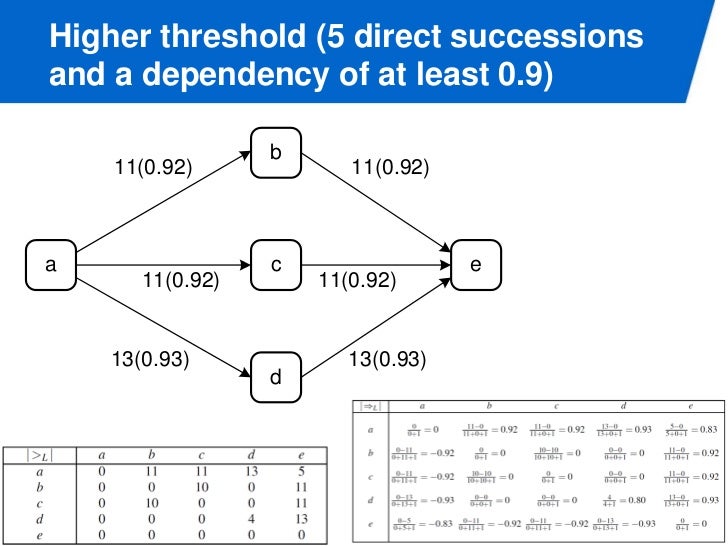
dependency measure a => b direct succession a > b 값을 이용해서 sequence, AND split, join, XOR join, split 등의 패턴을 파악할 수 있다.
게다가 a => a 도 값을 세기 때문에 loop pattern 도 발견할 수 있다
Learning C-nets
휴리스틱 마이닝의 두번째 단계는 split, join 등을 파악해서 C-nets 을 만드는 것이다.
어떻게 split, join 을 파악할까? 자주 사용하는 두 가지 접근 법이 있다.
(1) Heuristics approaches: using a time window before and after each activity. By counting sets of input and output acivities the bindings can be determinded (local decision)
(2) Optimization approaches: based on replay, Given a set of possible input and ouput bindings one can see whether reality can be replayed property. The set of possible input and output bindings are finite, so a “best set bindings” can be determined using some goal function.
Approach 1: Based on heuristics
dependency graph 에서 볼 수 있듯이 각 activity 는 가능한 input, output 이 있다. 얼마나 자주 나오는지 세면 된다. 이 때 어느 범위까지 셀지를 window size 라 부른다.
예를 들어 window size = 4 면
1 ... klbg[a]dhek ...
2 ... lkgc[a]hedl ...
3 ... kblg[a]ehdk ...
4 ... klgb[a]dehk ...
5 ... klkc[a]dkeh ...
이 때 b, c 에 대해서 {b} = 3, {c} = 2 다. 요게 input binding
{d, e} = 5 다. 요게 output binding. 이 값들을 depdency graph 를 표시하면 된다.
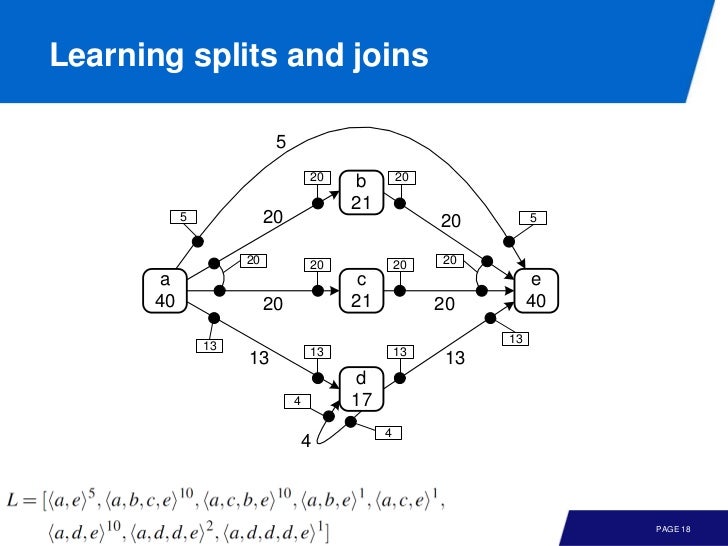
이걸로 끝나는것은 아니고 refinement 가 필요하다.
- What if there are no corresponding acivities in the input or output window?
- Noise filtering (remove infreq bindings)
- Handling repeating activities (cut off window size)
- Details are out of scope, but be aware of such complications when interpreting result
Approache 2: Optimization problem
- Evaluate all possible acivity bindings and take best one.
- Based on the idea that ideally a trace can be replayed from the initial input state to the final state
- This can be checked precisely using various replay approaches
- Hence, one can use approaches that simply try bindings exhaustively
간단히 말해서 가능한 모든 조합을 구하고, 말이 될 만한 input, output 을 replay 를 통해 골라내면 된다.
여기서 평가 기준은 fitness simplicity, precision, generalization 등이다. 시간이 너무 걸린다면 randomize, genetic algorithm 등을 이용할 수 있다. (generic 이 아니고 genetic 이다.)
Learning Transition System
지금까지 모델을 만들기 위해 다음의 방법을 배웠다.
- Alpha algorithm
- Heuristic mining dep graph, C-net
이번시간엔 state-based regions 를 배워보자.
(1) Learning a transition system using a state abstraction => transition system
(2) Transform the transition system into an equivalent Petri net => Petri net
(3) visualize (and convert if needed) => BPMN, etc.
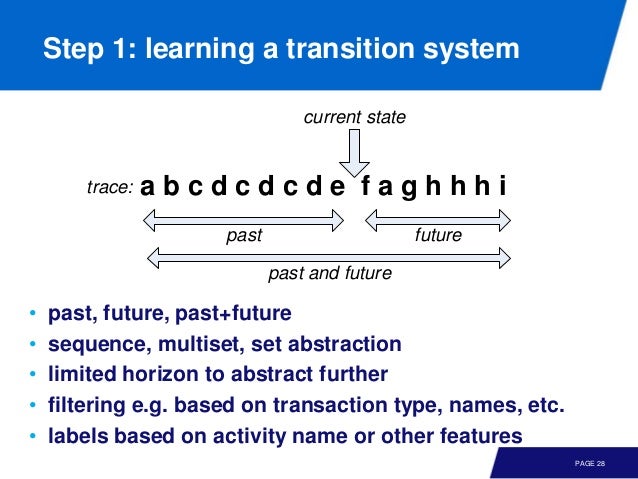
트랜지션 시스템을 학습하는 방법은, 현재 state 를 기준으로 past, future 를 보고 이 두가지를 합치면 된다. 말은 언제나 쉽다.
예를 들어 a b c d c d c d e ^ f a g h h h i 를 기준으로, 현재 상태가 ^ 라 하면
- past:
a b c d c d c d e - future:
f a g h h i
여기서 order 는 무시하고 frequency 만 고려하면 past 는
[a, b, c^3, d^3, e] 가 된다. 만약에, 여기서 time window (k-tail) 를 이용하면 [c, d^2, e] 가 된다.
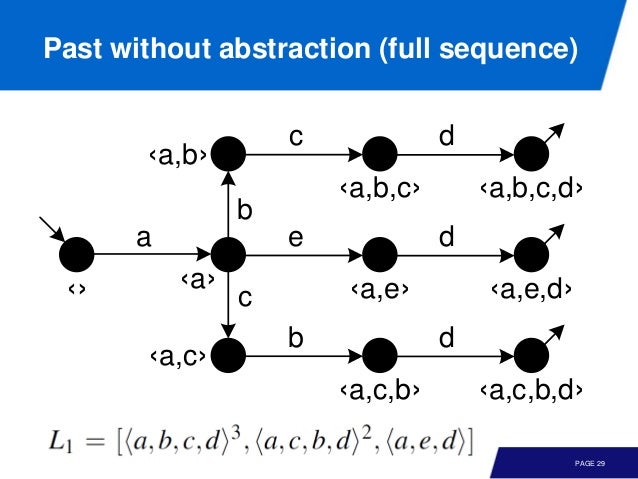


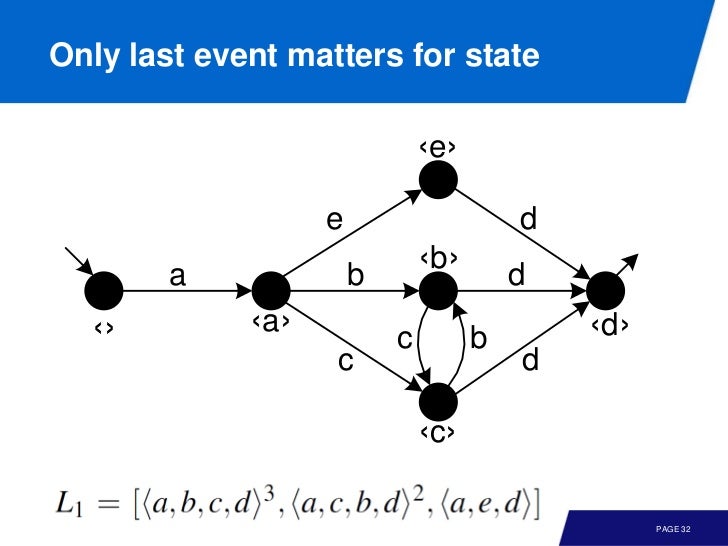
Postprocessing
- remove self-loop
- imporve diamond structure (for missing interleavings)
- merge similar states based on inputs
Using Regions to Discover Concurrency
이제 transition system 을 Petri net 으로 변경하면 된다.
기본적인 아이디어는 transition system 의 subset 이 Petri net 의 place 의 해당한다는 것이다. 이는 당연한데 트랜지션 시스템에서 어떤 상태는, 이 전까지의 상태의 반영이고, 이건 place 다.
State-based regions correspond to places
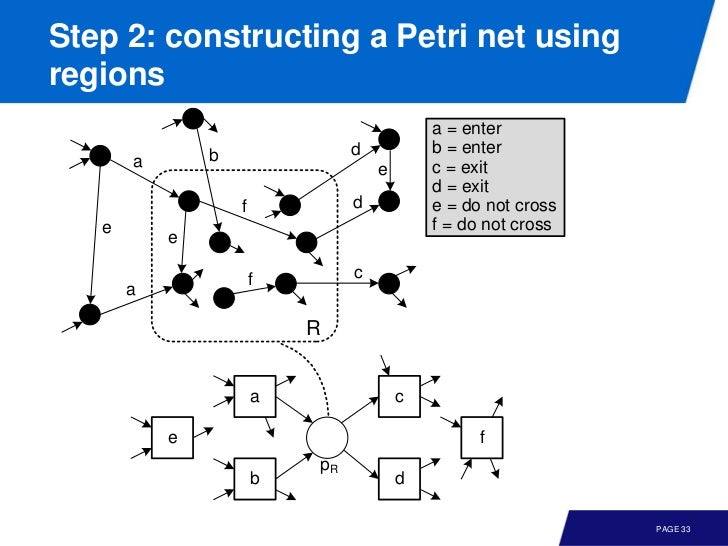
이 때 state-based region 의 enter, exit 를 확인 하면 쉽게 place 를 만들 수 있다.
All states need to be reachable
A region is a set of states, such that, if a transition exits the region, then all equally labeled trasition exit the region
and If a transition enters the region, then all equally labeled transitions enter the region
All events not entering or exiting the region do not cross the region
n 개의 concurrent activity 가 있으면 2^n 개의 state 가 생긴다. 이 때 몇 개의 region 이 생길까?
아무리 많아봐야 1 개의 트랜지션 라벨만 crossing 할 수 있으므로, n split 을 만들 수 있고 여기에 empty 까지 더하면 2(n + 1) 이다.
직선인 petri net 의 경우는 더 심각하다. 모든 transition 의 subset 이 region 이므로 2^(n+1) 이 된다. 따라서 non-trivial minimal region 만 포함해야 한다.
Petri net 을 만드는 알고리즘은
(1) For each transition label in the transition system, a transition is added to the Petri net
(2) The minimal non-trivial regions are computed
(3) For each minimal non-trivial region in the transition system, a place is added to the Petri net.
(4) The coressponding arcs are generated
(5) A token is aded to each place that corresponds to a region containing the initial state
L = [<a, c, d>^45, <b, c, e>^42]
의 경우 알파 알고리즘은 non directed dependency 를 발견하지 못하는데, 트랜지션 시스템을 만들고, state-based region 을 이용하면 올바른 petri net 을 만들 수 있다.
References
(1) Book: Process Mining
(2) Slide
(3) Process Mining: Data science in Action by Wil van der Aalst
(4) www.processmining.org
(5) http://fluxicon.com
(6) Confusion matrix
(7) Wikipedia - BPMN
(8) BPMN Gateway
(9) http://www.ijmijournal.com
comments powered by Disqus