Data Analysis Process Mining 2: Alpha Algorithm

Process Mining 2: Alpha Algorithm

지난 주 수업을 듣고 보니, 이벤트 로그를 만들어서 악성 사용자나, 비 정상적인 유저의 행동으로 부터 모델을 만들어서 어뷰징을 막거나, 부족한점을 개선해 서비스의 품질을 높일수도 있겠단 생각이 들었다.

근데 프로세스 마이닝에서 사용하는 이벤트 로그를 만들려면 activity 가 어떤 데이터가 되야할지 부터 정해야 하는데, 쉽지가 않다. 2주차에는 이런 고민들을 좀 해 보고, 프로세스 마이닝에서 사용하는 모델 표기법과 알파 알고리즘에 대해 논의한다.

(http://www.triua.com/)

Event Logs and Process Models

지난 시간에 Play-in, Play-out, Replay 에 대해 잠깐 언급했는데, 이 중에서 Play-in 은 사람들이 정해진 규칙에 의해서가 아니라, 실제로 따르는 프로세스를 찾아낼 수 있다.

Process discovery: learning de facto process models from observed behavior

그리고 Replay 는 conformance checking, prediction, bottleneck analysis 에 사용할 수 있다.

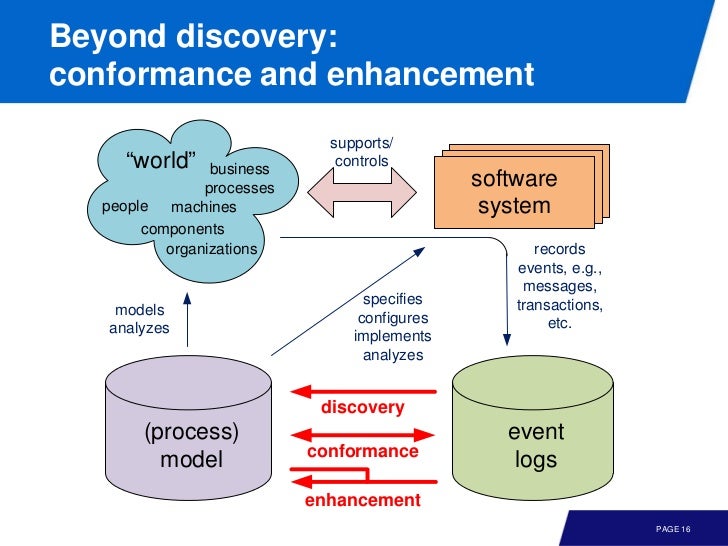
(www.procesmining.org)

결국 observed behavior 의 기록인 event-log 를 모으는 것이 중요하다. 그런데, 모든 이벤트를 바로 case id, activity name, timestamp 로 매핑하긴 쉬운 일이 아니다.

예를 들어 이메일에서 activity 는 무엇일까? ~~어렵다.~~ 다양한 답이 나올 수 있지만, 딱 맘에 드는 답을 찾기 어렵다.

transactional information 에서는 event 가 다양한 state (상태) 로 나타날 수 있다.

(http://architects.dzone.com)

한 가지 더 생각해 볼 문제는 case vs event 다. case 는 birth date 처럼 변하지 않는 것이고, event 는 프로세스를 거치면서 변하는 속성들이다.

이벤트를 정의하는데 다양한 방법이 있어 혼란스러울 수 있겠지만, 다행히도 프로세스 마이닝에서 사용되는 표준 포맷이 있다. eXtensible Event Stream, XES 인데,

(http://fluxicon.com)

control flow 를 표현하는데는 다양한 방법이 있다. BPMN, UML, Patri net 등등..

(http://en.wikipedia.org/wiki/Petri_net)

이 표기법들을 선택하는데 2가지 기준을 세울 수 있다.

(1) search space: finding a model that captures reality well
(2) visualization: what do end-users need to see?

선택된 표기법이 reality 를 잘 반영하지 못할 수 있기 때문에, 다양한 표기법들을 알고, 사용해 보는것이 정말 중요하다.

Petri Nets

(http://en.wikipedia.org/wiki/Petri_net)

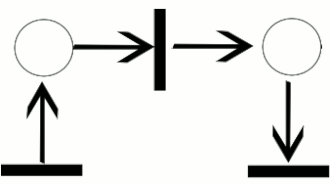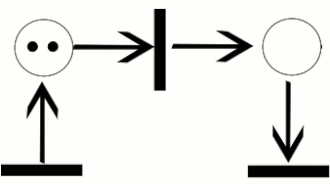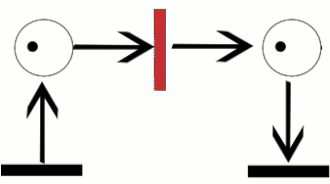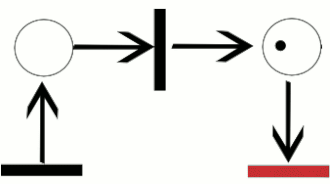
Petri Net 은 token, place, transition, arc 로 구성되어있다. 토큰은 한 place 에서 다음 place 로 이동할 수 있다. petri net 의 상태를 marking 이라 부른다.

transition 의 경우 input place 가 토큰을 담고 있어야만 다음 place 로 토큰을 옮긴다. 다시 말해서 transition 이 token 을 input places 로 부터 consume 해서 output place 에 token 을 produce 한다.

독립적인 transition 이 있을때 모든 transition 은 동시에 작동할 수도, 하나씩만 작동할 수도 있다.

신호등을 모델링 해보면 place 는 red, green,orange 이고 transition 은 rg, go, or 이다.

(http://www.bpm-book.com)

하나의 신호등은 정말 그리기 쉬운데, 두개의 신호등을 모델링 하려면 좀 골치가 아프다. 우선 두개의 petri net 을 따로따로 사용할건가, 토큰만 두개로 늘릴건가를 생각해보자.

토큰이 두개인 경우는 하나의 신호등이 green 이고 다른 신호등이 red 인 경우, 어떤 신호등이 green 인지를 알려주지 않는다. marking 이 6가지가 나온다.

반면 두개의 petri net 을 사용하면 marking 이 9 가지가 되어 순서가 보존된다. 순열과 조합의 차이라 보면 되겠다.

근데, 두개의 petri net 을 사용하면 두 토큰이 동시에 green 에 있을 수 있다. 이건 교차로라면 교통사고를 야기할 수 있다.

그리고 한가지 더 생각해 볼 문제는 신호등의 순서다. non-deterministic 이면 한 신호등만 주구장창 파란불, 빨간불, 파란불, 이 될 수 있다. 따라서 한 신호등이 변하면 다음 신호등이 변하는 모델을 만들어야한다.

Reachability Graph

transition 에 따라 marking 이 변하는 그래프를 그릴 수 있는데, 이것을 reachability graph 라고 부른다. 이 그래프 내에서 각 상태가 reachable marking 이다.

Transition Systems and Petri Net Properties

reachability graph 는 한 상태에서 다른 상태로의 전환을 표현하므로 transition system 이라 볼 수 있다. 그리고, *reachability graph*는 finite or infinite 모두 가능하다.

Boundedness, Safeness

어떤 place 에 k 이상의 토큰이 존재하는 reachable marking 이 없으면 k-bounded place 라 부른다. 쉽게 생각하서 upper bound 라 보면 된다.

만약에 petri net 의 모든 place 가 k-bounded 면, 그 petri net 도 k-bounded 다.

이런 k 가 petri net 이나 place 가 있을수도 있고, 없을때도 있는데, 있을때만 bounded petri net, bounded place 라 부른다.

만약에 어떤 petri net 이 1-bounded 면 safe 하다고 말한다.

Deadlock

그리고, dead marking 은 더이상 적용 가능한 transition 이 없을때다. 그리고 petri net 에 reachable dead marking 이 있으면 잠재적으로 deadlock 이 발생할 수 있다.

따라서 모든 reachable marking 이 적어도 하나의 transition 이 있을때 deadlock free 하다고 말할 수 있다.

Safeness

어떤 transition t 대해, 어느 reachable marking 에서도 t 를 적용가능하면 t 는 live 하다. 그리고 모든 트랜지션이 live 면, petri net 은 live 다.

live petri net 에서는 모든 트랜지션이 적용 가능하므로 deadlock-free 하다고 말할 수 있다.

Transition System

이전에 보았던 reachability graph 는 transition system 의 특별한 종류다. 트랜지션 시스템은 state 와 transitions 로 구성되는데, 하나 이상의 initial state 와 0 개 이상의 final states 가 있다.

이 때 initial state -> final state 로의 path 를 complete trace 라 부른다.

모델로 부터 transition system 을 만들고 이것으로 부터 complete trace 를 만들 수 있는데, 문제는 트랜지션 시스템이 엄청나게 거대해 질 수 있거나 심지어는 무한할수도 있다는 사실이다.

단순히 (token) -> a1 -> () 이란 간단한 모델에서 a1, ..., ak 만 해도 2^k 개의 트랜지션 시스템이 나온다. 어마어마하다

Workflow Nets and Soundness

Petri net 은 간편하긴 한데, 위에서 말했듯이 무한한 트랜지션 시스템이 나올 수 있고, 데드락이 발생할 수도 있다.

따라서 프로세스 마이닝에서는 모델을 만들기 위해 end state 가 있고, 위에서 언급한 anomalies 가 없는 Petri net 의 일종인 Workflow Nets, WF-Nets 를 사용하기도 한다.

(http://www.bpm-book.com)

본래 WF-nets 은 BPM 에서 쓰이던 것이다. BPM 은 IT 와 비즈니스를 연결해 주는 학문인데,

(http://bpmcenter.org/)

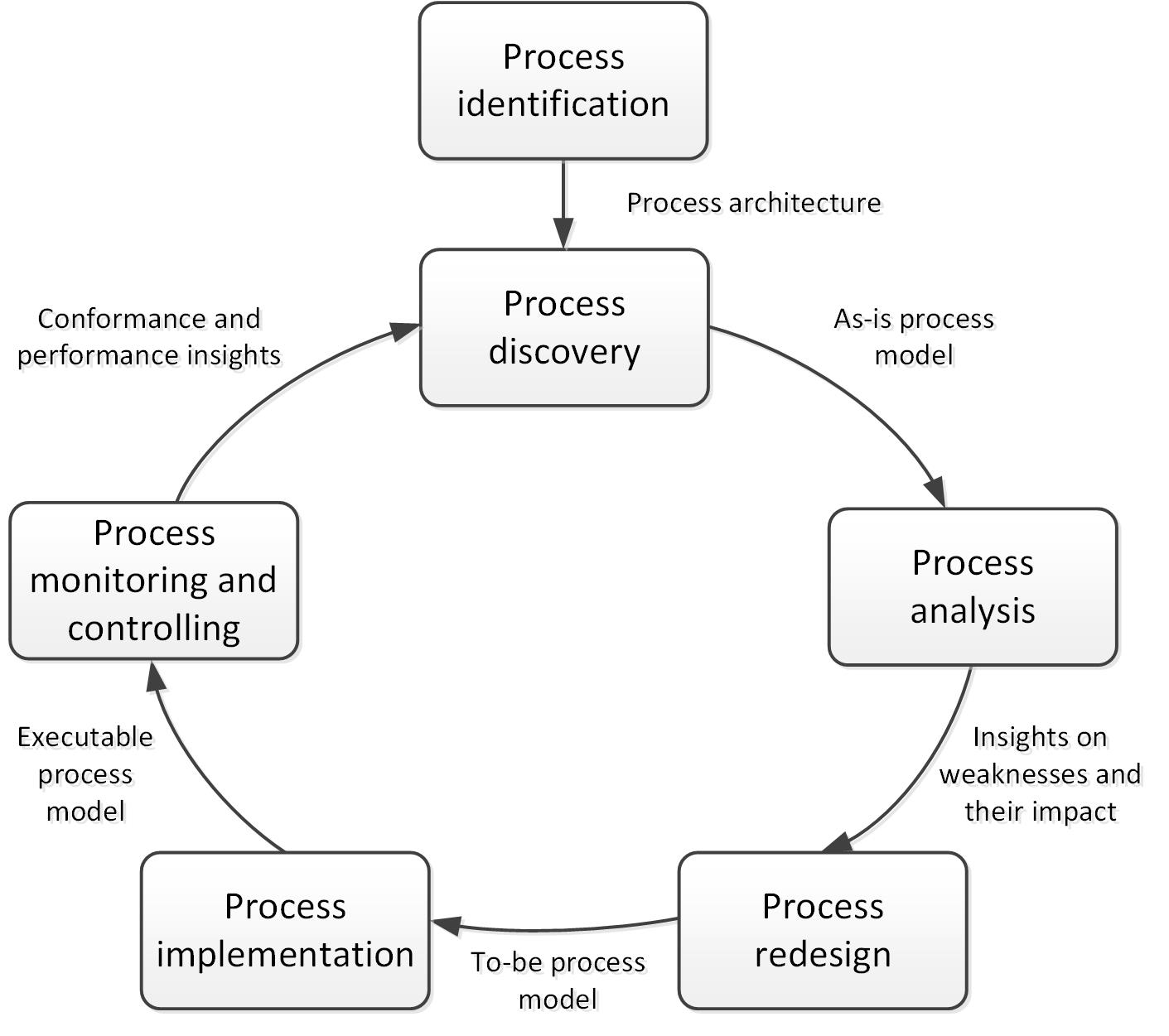
model-based analysis 와 data-based analysis 를 반복하면서 모델을 개선한다.

BPM 에서 모델의 역할은

(1) reason about processes (redesign)
(2) make decisions inside processes (planning and control)

안타깝게도 모델을 표현하는데 다양한 notation 이 있다. (언급 했듯이 search space 와 visualization 때문) 이 수업에서는 3 가지 표기를 사용한다.

Business Process Model and Notation (BPMN)
Event-Driven Process Chains (EPCs)
Petri nets (Workflow nets)

아래 이미지는 각각, BPMN, EPCs 다.

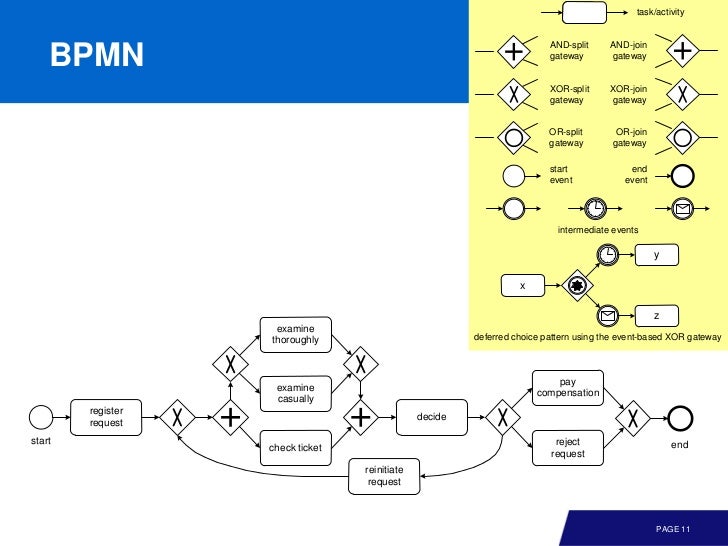
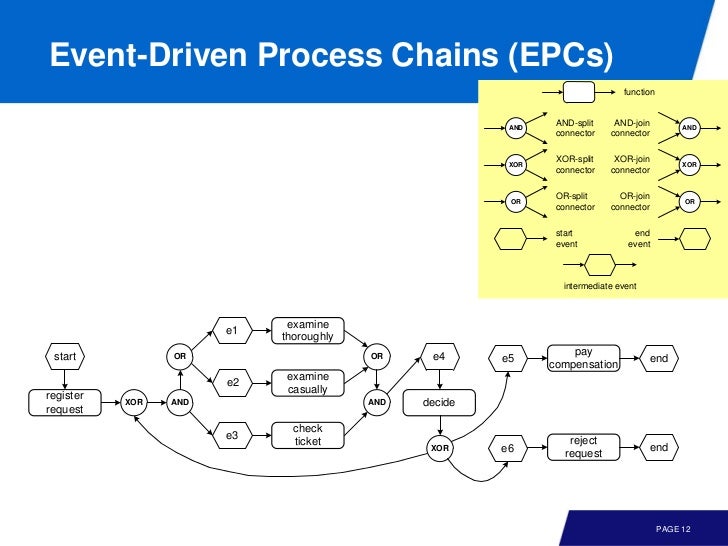
Good Model

좋은 모델이란 일반적으로 sound WF-net 을 말한다.

Workflow net 이란

A Workflow net has one source place(start) and one sink place(end) and all other nodes are on a path from source to sink.

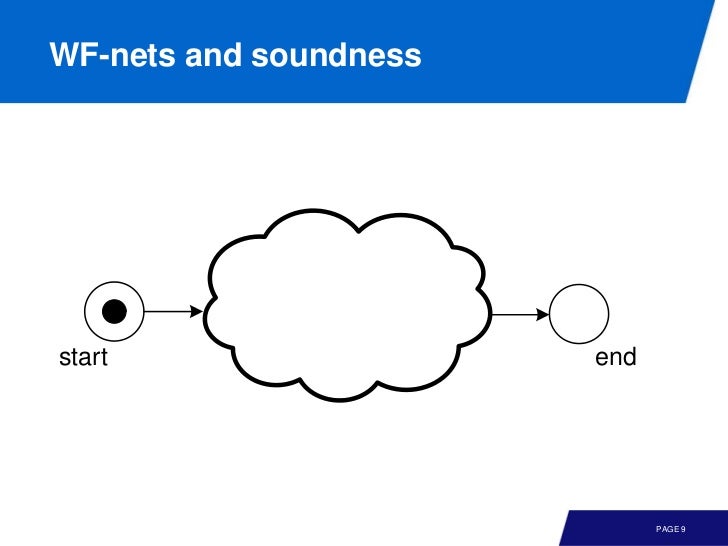
Workflow net 이 sound 라는건

A workflow net is sound if and only if the following properties hold:

(1) safeness: places cannot hold multiple tokens at the same time
(2) proper completion: if the sink place is marked, all other places are empty
(3) option to complete: it is always possible to reach the marking that marks just the sink place
(4) absence of dead parts: for any transition there is a firing sequence enabling it

작은 모델은 soundness 를 검사하기 쉬울지 모르지만, 모델이 커지만 좀 힘들 수도 있다. 여기에 사용할 수 있는 몇 가지 테크닉이 있다.

(1) 우선 option to complete 와 proper completion 을 보면, proper completion 이 거짓이면 option to complete 도 거짓이므로 검사할 필요가 없다. 반대로 option to complete 가 참이면 Iproper completion 도 참이다.

option to complete impiles proper completion

(2) 만약 WF-net 의 end 에서 start 로 트랜지션을 만든 short-circuited petri net 이 live, bounded 면 WF-net 은 sound 다.

A WF-net is sound if and only if the corresponding “short circuted” Petri net is live and bounded

Model-based Analysis

위에서 본 soundness checking 같은 검증이나 performance analysis 같은 시뮬레이션이 모델-베이스드 분석해서 주로 하는 일이다. 근데, 이런 검증이나 시뮬레이션은 모델이 높은 퀄리티를 가져야만 한다는 한계가 있다. 프로세스 마이닝은 이런 모델기반 분석과 실제 데이터를 연관시킨다.

Alpha Algorithm

alpha algorithm 을 이용해서 모델을 발견할 수 있다. 즉 아래 그림에서, discovery 에 해당하는 과정이다. 이벤트로그로 부터 모델을 만드는 과정을 play-in 이라 부르기도 한다.

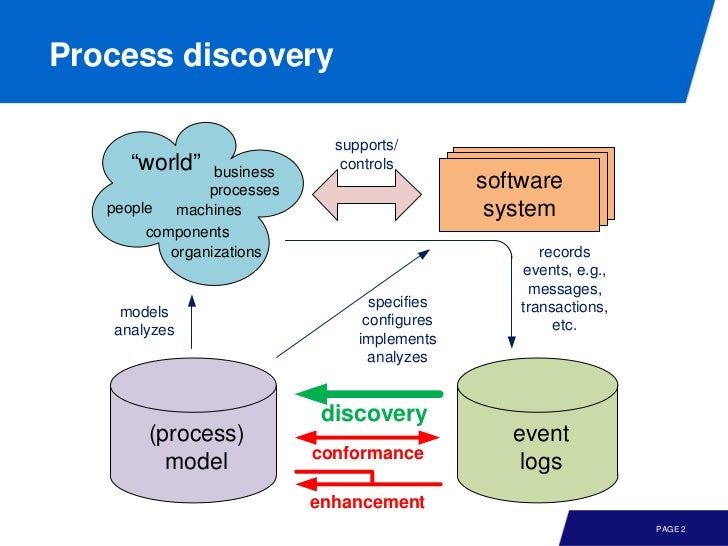
이벤트 로그를 간략화 하면 activity 의 order 가 된다. 즉, timestamp 가 order 로 표현되고, 한 묶음의 ordered activity 가 모여서 trace 가 된다. 예를 들어서 다음은 이벤트 로그라 볼 수 있다.

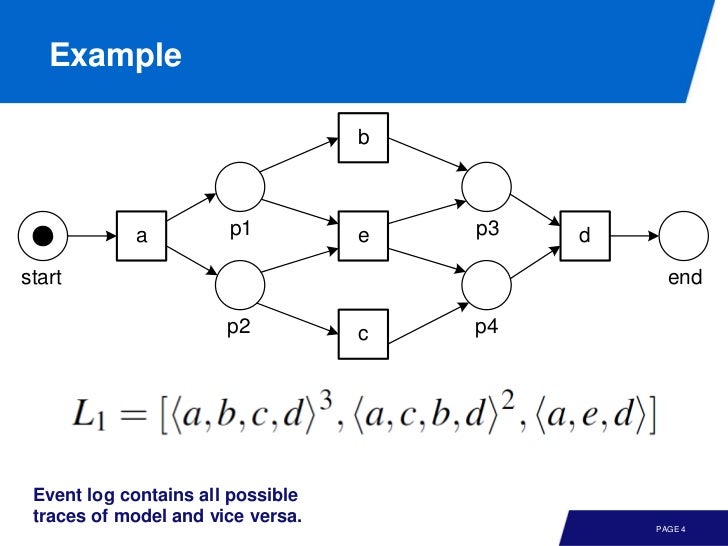
알파 알고리즘의 목적은 이렇게 간략화된 이벤트 로그를 이용해 모델을 뽑아내는 것이다.

Operations

몇 가지 연산자를 알고 넘어가자

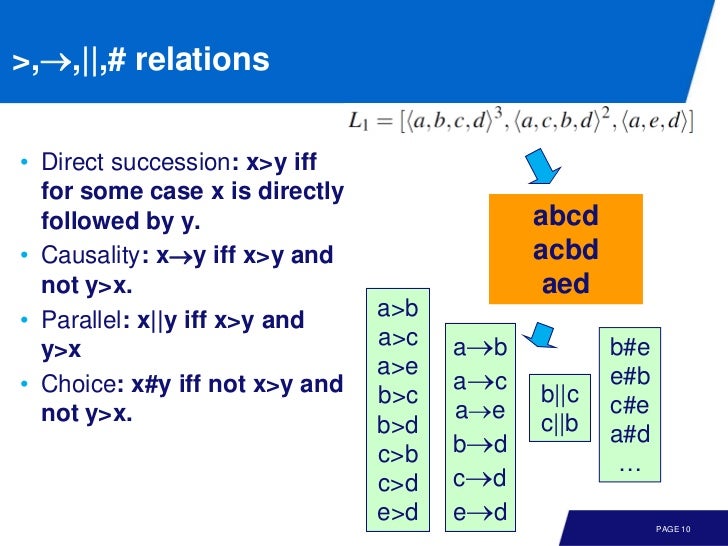
(1) direct succession: x > y, iff for some case x is directly followed by y
(2) causality: x -> y, iff x > y and not y > x
(3) parallel: x || y, iff x > y and y > x
(4) choice: x # y, iff not x > y and y > x

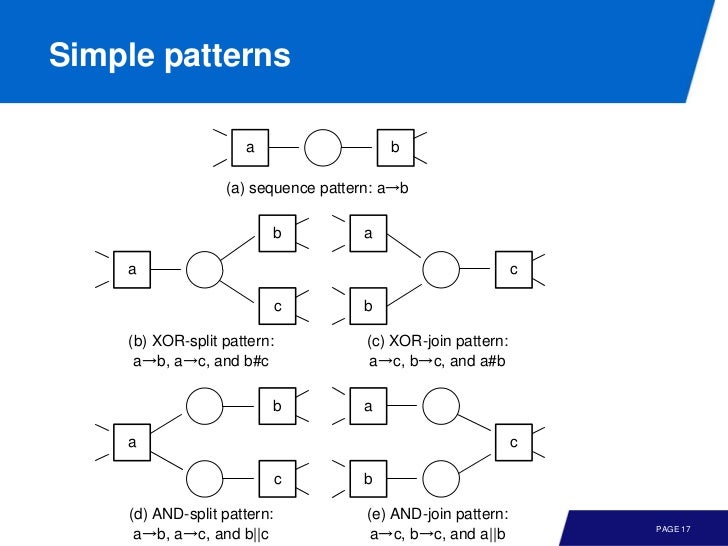
그러면 이 연산자를 조합해 패턴을 발견할 수 있다.

(1) sequence: a -> b
(2) XOR split: a -> b, a -> c, b # c
(3) XOR join: b -> d, c -> d, b # c
(4) AND split: a -> b, a -> c, b || c
(5) AND join: b -> d, c -> d, b || c

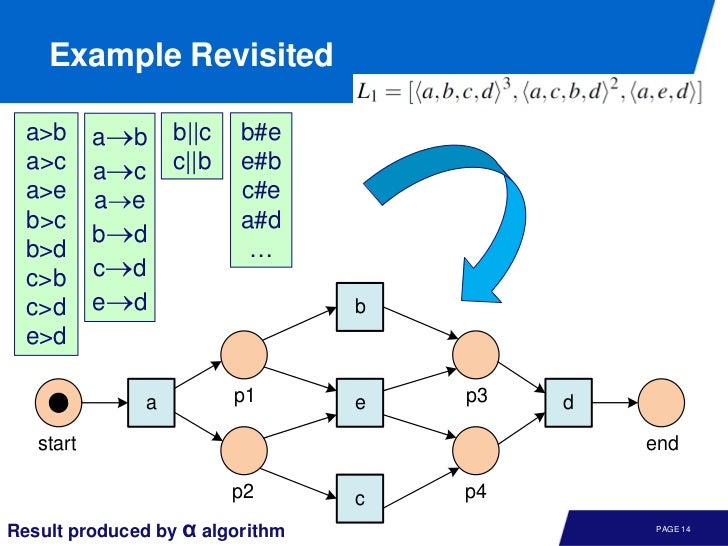
Footprint

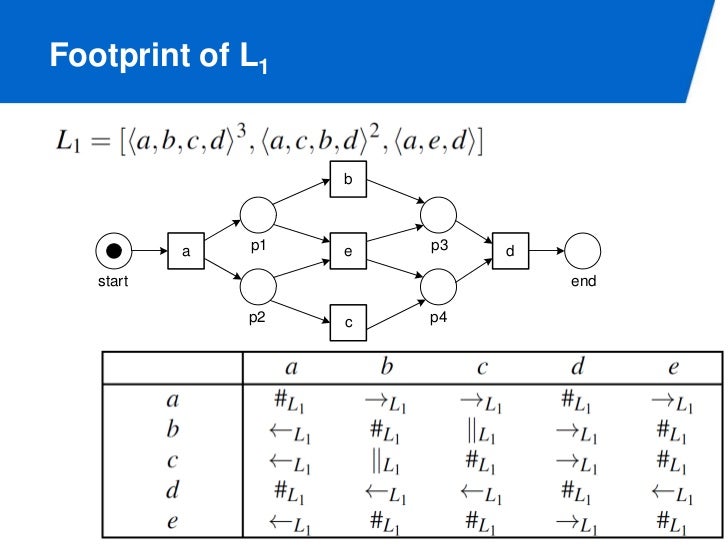
각 트랜지션 사이에 테이블을 하나 만들면 이처럼 생겼는데, footprint 라 부른다. 우리가 로그를 이용해 만든 모델과, 로그의 풋 프린트는 동일하다.

Log and model agree on footprint

Logics

알파 알고리즘은 이렇게 생겼는데, 너무 개략적으로 설명해 주셔서 나도 개략적으로 밖에 알지 못한다. 간략히 설명하면

(1) activity 를 transition 으로 매핑한다
(2) 첫 번째 트랜지션을 찾는다
(3) 마지막 트랜지션을 찾는다

두 인접한 트랜지션 사이에 있는 것은 place 이므로, 두 인접한 트랜지션을 찾아보자. 먼저

(4) (A, B) 를 계산한다

이 때 A 내에 있는 모든 a 와 B 내에 있는 모든 b 에 대해 a > b 이고, a1 # a2, b1 # b2 인 (A, B) 를 찾는다.

Find paris (A, B) of sets of activities such as that every element a in A and every element b in B are causally related, all element in A are independent and all elements in B are independent

(5) non-maximal pair 를 제거한다.

(4) 에서 찾은 (A, B) 는 부분집합을 가질 수 있다. 이러면 sub-pair 로 인해 place 가 또 생길 수 있으므로 제거한다.

예를 들어 [({b}, {d}), ({b, e}, {d})] 이 있다면 sub-pair ({b}, {d}) 를 제거한다.

Delete from set X_L all paris (A, B) that are not maximal

(6) place P_(A, B) 의 위치를 결정한다.

Determine the place set. Each element (A, B) is a place. To ensure the workflow structure, add a source place and target place

(7) (2) 와 (3) 에서 찾은 출발점과 끝점과 (6) 에서 찾은 place 의 source transition 과 target transition 과 잇는다.

Determine the flow relation. Connect each place P(A, B) with each element a of its set A of source transitions and with each element of its set B of target transitions. In addition, draw an arc from the source place to each start transition and an arc from each end transition to the sink place

따라서 전체적인 알고리즘은

먼저 footprint 를 만들고
여기서 집합 내부적으로 # 이고 집합간 > 를 가지는 (A, B) 를 구한뒤
중복을 제거하기 위해 non-maximal pair 를 제거한다
(A, B) 에서 하나씩 pair 를 뽑아서 잇고, 이것들과 초기 트랜지션 T_I, 마지막 트랜지션 T_O 와 잇는다.

Intuition

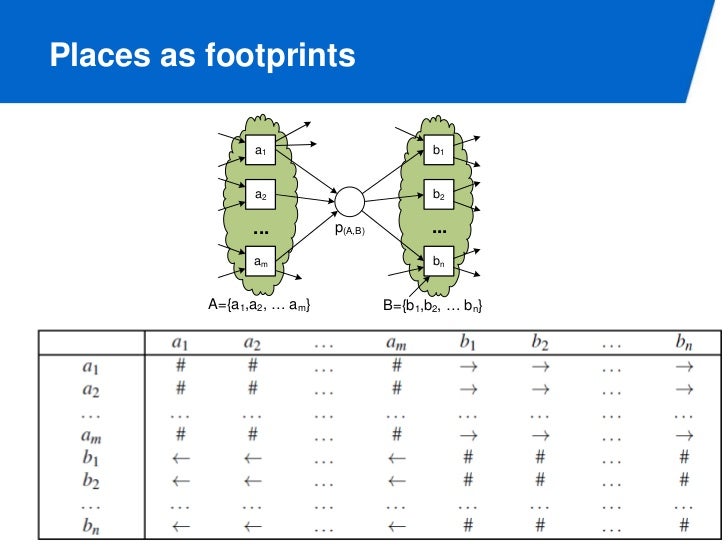
알파 알고리즘은 간단하지만 loop, choice, concurrenc 등 꽤 많은 연산을 찾아낸다. 그러나 한계가 있다.

Limitation

implicit places

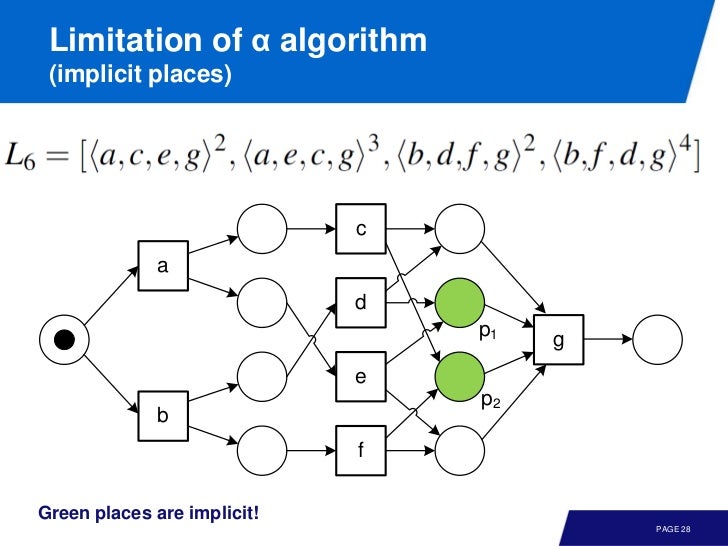
여기서 초록색 place 는 아무일도 하지 않음에도 alpha algorithm 이 찾아냈다.

Loops of length 1, 2

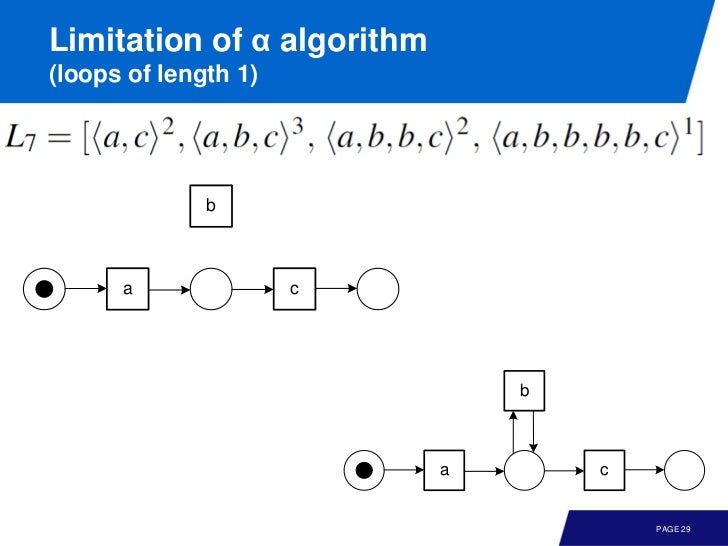
이벤트 로그를 보면 실제로는 b 가 self-loop 가 있음에도 알파 알고리즘은 찾아내지 못한다.

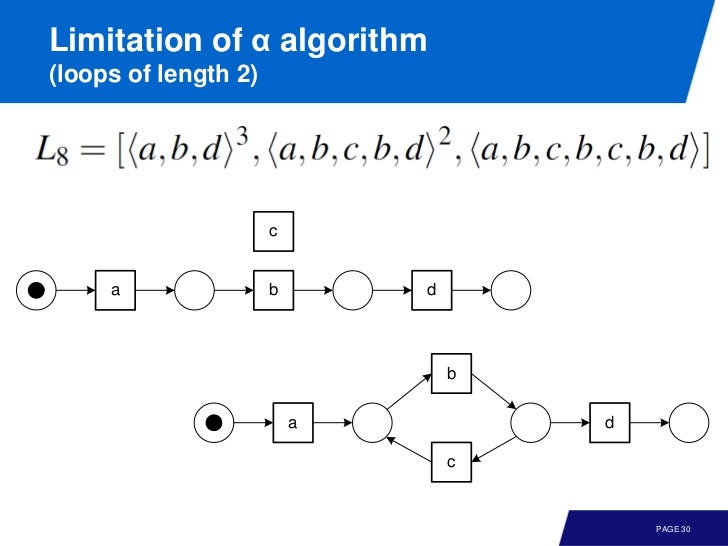
길이가 2인 루프도 마찬가지로 찾아내지 못한다.

Non-local dependency

여기서 알파 알고리즘을 돌리면 p1, p2 를 못찾는다. 아래 그림은 알파 알고리즘이 찾기 힘든 모델이다.

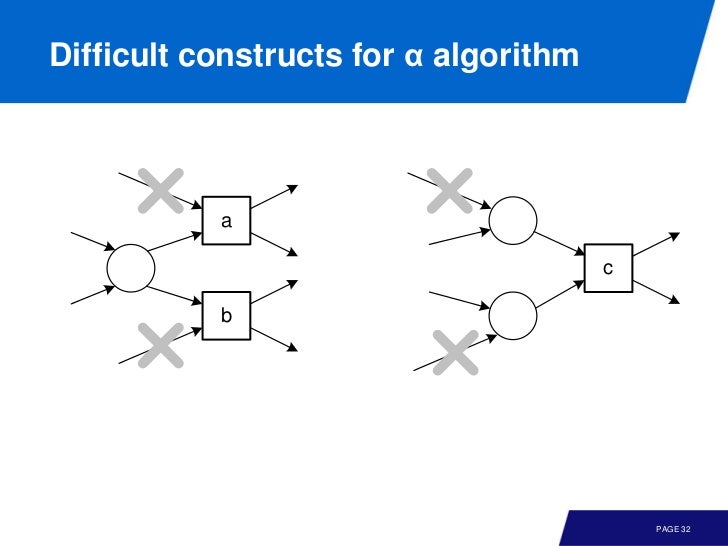
Representation Bias

알파 알고리즘이 가지는 표현적인 한계 때문에 다음과 같은 경우도 발생한다.

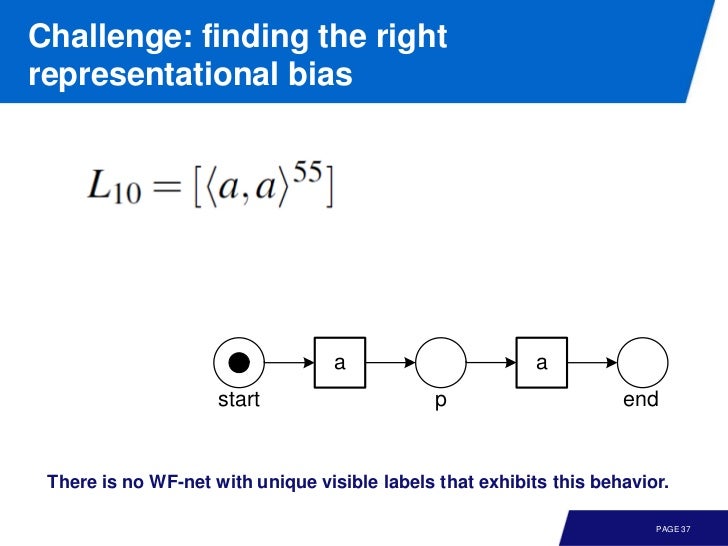
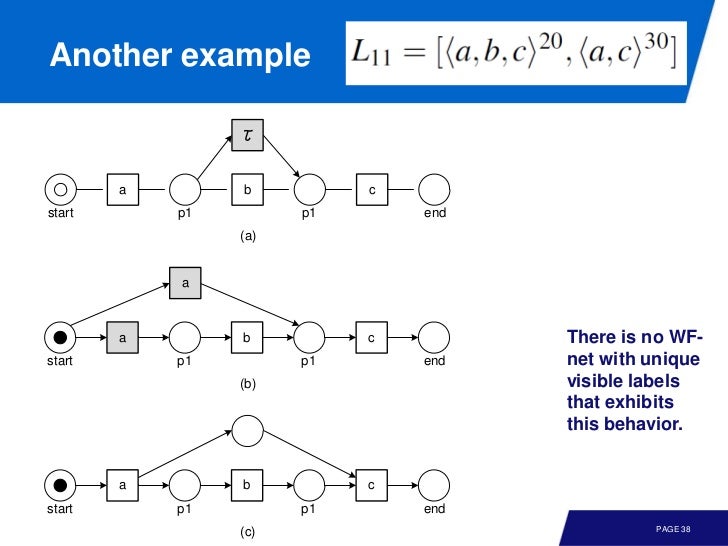
Noise and Incompleteness

알파 알고리즘은 아주 기본적인 알고리즘이기 때문에 패턴을 잘못 인식하는 경우가 많다.

게다가, 이벤트 로그 자체가 완벽한 trace 가 아닐수도 있다는 것도 고려해야한다.

Noise: the event log contains rare and infrequent behavior not representative for the typical behavior of the process

Incompleteness: the event log contains too few events to be able to discover some of the underlying control-flow structures

즉 이벤트 로그 자체가 어떤 패턴을 발견하기엔 너무 적거나, 좀 노이지할 수가 있다는 뜻이다.

Fitness vs Precision, Simplicity vs Generalization

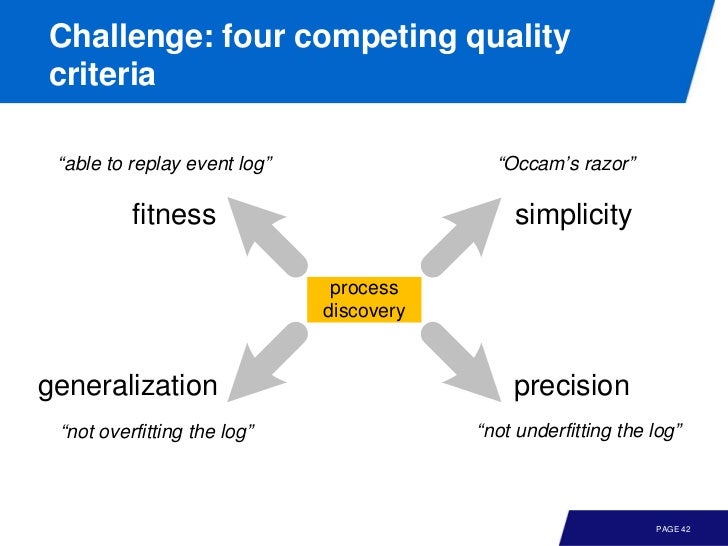
아래의 두 모델중 어떤게 더 이벤트 로그를 잘 반영한 것일까? 빈도가 적은 로그는 표현하지 않는것이 더 좋은가?

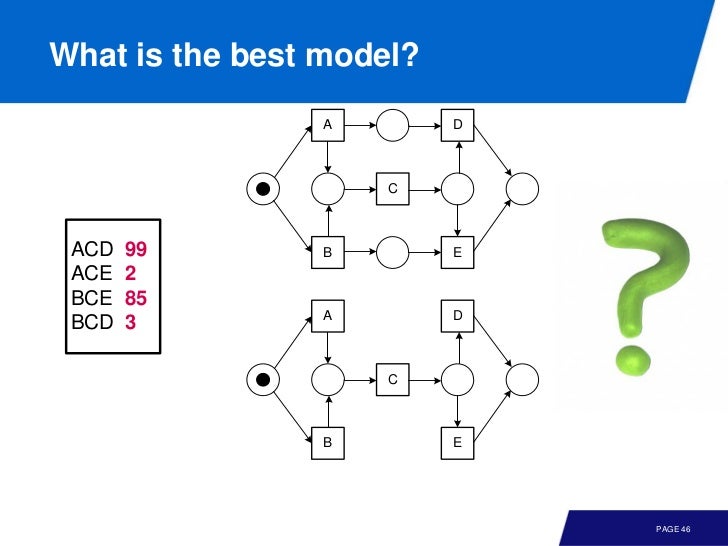
Summary

루프가 있거나, 모델에 parallel 이 있는 경우에 가능한 trace 의 수는 기하 급수적으로 많아진다.

그러나 우리가 가진 이벤트 로그는 일부분이다. 따라서 이런 로그로 만드는 모델은 어느정도 틀릴 수 밖에 없다.

알파 알고리즘의 단점을 좀 정리해 보면,

(1) implicit places: harmless and be solved through preprocessing
(2) loops of length 1: can be solved in multiple ways
(3) loops of length 2: idem.
(4) non-local dependencies: challenging
(5) representational bias: cannot discover transtions with duplicate or invisible labels. other algorithms may have a different bias.
(6) discovered model does not need to be sound: some algorithm ensure this.
(7) noise, incompleteness: challenging

References

(0) Book: Process Mining
(1) Slide
(2) Process Mining: Data science in Action by Wil van der Aalst
(3) www.processmining.org
(4) http://fluxicon.com
(5) http://en.wikipedia.org/wiki/Petri_net
(6) http://www.bpm-book.com
(7) http://bpmcenter.org/