Edit this page

Data Analysis ML 07: Support Vector Machine

ML 07: Support Vector Machine

이번시간에 Support Vector Machine, SVM 을 배운다.

Optimization Objective

먼저 직관을 얻기 위해 logistic regression 의 sigmoid function 을 좀 보자.

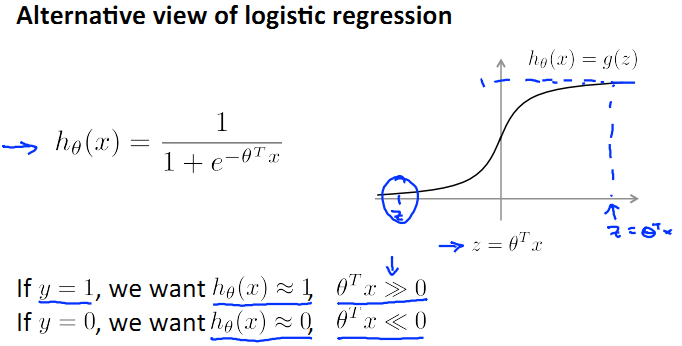
(http://blog.csdn.net/abcjennifer)

y = 1 이면 0^Tx >> 0 이어야 h(x) 가 1 에 가까워 진다.

이제 cost function 에 h(x) 를 넣자. 그리고 m = 1 인 트레이닝 셋에 대해서 보면

(http://blog.csdn.net/abcjennifer)

파란 그래프에서 볼 수 있듯이 y = 1 일때 0^Tx >> 0 이면 cost 가 상당히 낮아지는걸 볼 수 있다. 이 그래프를 좀 단순화 해서 자주색 그래프를 만들어 보자. 두개의 직선으로 만들었는데, 이 cost function 을 계산하면 상당히 근접한 값을 얻을 수 있고, 동시에 그래프가 단순해져 computational advantage 를 얻을 수 있다.

각각 좌측, 우측에 있는 cost function 을 이렇게 쓴다.

$\ \\cost_1(z)\ (y = 1) \\cost_0(z)\ (y = 0)$

logistic regression 식 에서 -log h(x) 를 cost_1(z) 로, -log(1 - h(x))) 를 cost_0(z) 로 바꾸면

$min_\theta \ {1 \over m} [\sum_{i=1}^m y^{(i)}(-log\ h_\theta(x^{(i)}))\ + \ (1 - y^{(i)})\ (-log(1\ -\ h_{\theta}(x^{(i)})))]\ + \ {\lambda \over 2m}\sum_{j=1}^n \theta_j^2 \\cost_1(z)\ (y = 1) \\cost_0(z)\ (y = 0)$

$\\cost_1(z)\ (y = 1) \\cost_0(z)\ (y = 0) \\ min_\theta \ {1 \over m} [\sum_{i=1}^m y^{(i)}cost_1(\theta^Tx)\ + \ (1 - y^{(i)})\ (cost_0(\theta^Tx))]\ + \ {\lambda \over 2m}\sum_{j=1}^n \theta_j^2$

이 때, 1/m 은 상수이므로 제거해도 어차피 똑같은 0(theta) 를 얻을 수 있다.

그리고 식을 좀 간략히 적어보면

$min_\theta \ A + \lambda B$

여기서 lambda 가 하는 일은 low cost (‘A’) 와 small parameter (‘B’) 를 조절하는 일이다. 식을 좀 변경하면 이렇게도 볼 수 있다. 여기서 C 는 1 / lambda 과 같은 역할이라 보면 된다.

$min_\theta \ C + \lambda B$

아주 작은 수의 lambda 를 사용하면 파라미터 B 가 커지는데, 이것은 C 가 커져 A 를 낮추고 B 를 높이는 것과 똑같다. 반대로 C 가 작으면 A 가 커지고, B 가 작아진다.

결국 C 를 쓰느냐 lambda 를 쓰느냐는, 어떤 항을 옵티마이제이션의 중심으로 두느냐다. 최적화된 파라미터를 찾는건 똑같다.

식을 마지막으로 정리하면,

$min_\theta \ C \ [\sum_{i=1}^m y^{(i)}cost_1(\theta^Tx)\ + \ (1 - y^{(i)})\ (cost_0(\theta^Tx))]\ + \ {1 \over 2}\sum_{j=1}^n \theta_j^2$

결국 위 식 (cost) 를 최소화 하면, y = 1 일때 0^Tx >> 0 이 되므로 h(x) == 1 이란 뜻이다.

(http://blog.csdn.net/abcjennifer)

Large Mingin Intuition

SVM 은 large margin classifier 라 부르도 한다. 왜 그런게 한번 살펴보자.

두 집단을 구분하는 초록색, 자주색, 검은색 직선을 생각해 보자.

(http://blog.csdn.net/abcjennifer)

검은색 선이 가장 낫고, 자주색과 초록색은 두 집단을 분리하긴 하는데 썩 만족할만하게는 아니다. 검은 선과 평행하고 각 점까지의 거리가 최소인 파란선을 그리자. 이걸 margin 이라 부른다. 다시 말해서 margin 이 클수록 좋은 classification 이다.

large margin 하고 SVM 하고 무슨 상관일까? 그 전에 먼저 C 를 좀 살펴보자.

(http://blog.csdn.net/abcjennifer)

z == 0^T x, 의 범위를 생각해 보면 y = 1 일때 z >= 1 이길 바란다. 반대로 y = 0 이면 z <= -1 이면 h(x) 로 충분히 만족할 만한 값을 얻을 수 있다.

이 때 C 가 매우 크면 A 즉, 아래의 식은 굉장히 작아진다. 거의 0 에 가깝게

$\sum_{i=1}^m y^{(i)}cost_1(\theta^Tx)\ + \ (1 - y^{(i)})\ (cost_0(\theta^Tx))$

(http://blog.csdn.net/abcjennifer)

두 집단에 대해서 C 가 매우 크면, 다시 말해 A 가 0 에 가까우면 overfitting 된다 볼 수 있으므로 자주색과 비슷한 라인을 찾아낸다. 자주색 선은 모든 샘플에 대해 large margin 을 가지고 있지만 그렇게 썩 좋은 classification 이라 볼 수는 없다.

그러나 C 가 그렇게 크지 않으면 비 정상적인 샘플들은 조금 무시하고 검은색 선을 찾아낸다. 이게 SVM 이 작동하는 방식이다.

Mathematics Behind Large Margin Classification

(http://blog.csdn.net/abcjennifer)

결국 C 가 아주 클 때 A = 0 이므로 SVM cost fucntion 을 최소화 하는 것은 아래 식과 동일하다. 그런데 이 식을 풀어 보면

$min_\theta \ {1 \over 2} \sum_{j=1}^n \theta_j^2 \\ \\ = {1 \over 2} \left \| \theta \right \|^2$

그리고 0(theta) 와 x 를 벡터이므로 0^T x^(i) = p^(i) * ||0|| 라 볼 수 있다. (여기서 p^(i) 는 x 의 0 로의 projection 된 선의 길이)

$\theta^Tx \\ \\ = p^{(i)} \left \| \theta \right \|$

이제 이 식을 좀 활용해 보자. C 가 매우 클때는 B 만 최소화 하면 되는데

$min_\theta \ {1 \over 2} \sum_{j=1}^n \theta_j^2$

이 식 자체가 large margin 을 찾아낸다. 왜 그런가 보면

(http://blog.csdn.net/abcjennifer)

왼쪽 그래프의 계산 과정을 보면 x1 을 0 에 projection 해서 얻은 p1 이 매우 작다. 따라서 p1 * ||0|| >= 1 에서 ||0|| 가 커야 전체 식이 1보다 커지는데, 이러면 식 B 를 최소화 할 수 없다. 마찬가지로 p2 는 매우 작은 음수고, p2 * ||0|| <= -1 에서, ||0|| 가 매우 큰 음수여야 한다. 이 또한 0 를 크게 만드므로 식 B 가 작아지는 0 를 찾지 못한다.

결국 p 가 커야만 0 가 작아지기 때문에 p 를 크게 하는 0 만 찾고, 이것은 large margin 이다. 따라서 초록색 같은 low margin 의 0 는 선택되지 않는다.

정리하자면 C 가 매우 클때 SVM 은 large magin 을 찾고, 여기서 C 를 낮춤으로써 적당한 수준의 classification 을 얻을 수 있다.

$min_\theta \ {1 \over 2} \sum_{j=1}^n \theta_j^2$

Kernels

(http://blog.csdn.net/abcjennifer)

SVM 으로 non-linear decision boundary 를 어떻게 찾아낼까? 단순히 high polynomial features 를 사용하는 것보다 더 나은 방법은 없을까? 고차 다항식은 이미지 처리 예제에서도 봤지만, 계산 비용이 너무 비싸다.

kernel 이란 개념이 있다.

(http://blog.csdn.net/abcjennifer)

수동으로 몇몇 landmark l1, l2, ... 을 고른후 이 landmark 사이와의 거리로 새로운 feature f 를 만든다.

$f_1 = similarity(x, l^{(1)}) = exp (- {||x-l^{(1)}||^2 \over 2\sigma^2})$

dl similarity function 을 kernel function 특히 여기서 사용한 수식은 gaussian kernel 이라 부른다.

(http://blog.csdn.net/abcjennifer)

x 와 l 이 상당히 가까우면 f 는 1 에 근접하고, 상당히 멀면 0 에 가까워진다.

(http://blog.csdn.net/abcjennifer)

위 그림은 시그마에 따른 f 값의 변화를 보여주는데, 시그마가 작으면 작을수록 조금만 멀어도 f 값은 0 에 가까워진다.

(http://blog.csdn.net/abcjennifer)

데이터가 landmark 중 하나에 라도 가까우면 적어도 하나의 f 가 1이 되어, h(x) 가 1 이되고 반면 모든 landmark 에 멀면 모든 f 가 0 이 되어 h(x) 가 0 이된다.

그럼 이제, 문제는 어떻게 landmark 를 정할 것인가?

(http://blog.csdn.net/abcjennifer)

l1, ..., lm 을 x1, ..., xm 라 하자. 즉 각 training example 이 landmark 가 된다. 이를 이용해 구한 feature vector f^(i) 중 하나는 sim(x^i, l^i) 이므로 1이 된다.

(http://blog.csdn.net/abcjennifer)

따라서 주어진 x 에 대해 m + 1 의 벡터 f 를 구해 0^Tf >= 0 이면 y = 1 이다. 그리고 이 때 feature 수가 m 이 되므로

$min_\theta \ C \ \sum_{y=1}^mcost_1(\theta^Tf^{(i)}) + (1-y^{(i)})cost_0(\theta^Tf^{(i)})) + {1 \over 2} \sum_{j=1}^m\theta_j^2$

마지막 항을 좀 자세히 보면

$\sum_{j=1}\theta_j^2 \\ \\ = \theta^T \theta$

인데 SVM 실제 구현에서는 가운데 M 매트릭스를 삽입해 좀더 효율적으로 돌아가도록 한다. 이 M 은 어떤 kernel 을 사용하는지에 따라 다르다.

$\theta^T M \ \theta$

logistic regression 에 kernel 을 사용할 수도 있겠지만, 상당히 느리다. 반면 SVM 에서는 마지막 항을 위 처럼 수정할 수 있기에 빠르게 동작한다.

Bias vs Variance in SVM

(http://blog.csdn.net/abcjennifer)

(1) C 가 크면 low bias, high variance (== small lambda)
(2) C 가 작으면 high bias, low variance (== large lambda)

sigma 가 크면 f 가 적게 변하기 때문에 인풋 x 에 대해서도 high bias, low variance 다.

Using an SVM

(http://blog.csdn.net/abcjennifer)

라이브러리를 사용하더라도 C 와 어떤 kernel 을 사용할지는 골라야 한다.

feature 가 크고, 트레이닝셋이 작을때는 overfitting 될 수 있으므로 linear kernel 을 사용하는 편이 낫다.

반면 n 이 작고, m 이 클 경우에는 non-linear 가설일 수 있으므로 gaussian kernel 을 사용할 수 있다. 그러면 sigma 를 골라야 한다.

(http://blog.csdn.net/abcjennifer)

SVM 라이브러리를 이용할때는 kernel function 을 직접 구현해야 한다. 이걸 이용해서 라이브러리는 x 에 대해 f1, ..., fl 을 계산한다.

만약에 feature 의 스케일이 다르면, x1 = 10000, x2 = 5, ... ||x-l||^2 값이 숫자가 큰 항에 의해 좌우될 수 있으므로 feature scailing 을 하는편이 좋다.

Other choices of kernel

(http://blog.csdn.net/abcjennifer)

SVM 구현들이 계산을 최적화 하기위해 다양한 트릭을 이용한다. 이로 인해 모든 similarity function 유효한 커널이 되는건 아니고, “Mercer’s Theorem” 을 만족해야만 한다. ~~인용하려 했는데 무슨말인지 모르겠음~~

그렇다고 커널이 linear 와 gaussian 만 있는건 아니고 다양한 커널이 있다. 그림을 참조하자.

Multi-class classification

(http://blog.csdn.net/abcjennifer)

대부분의 SVM 라이브러리들은 multi-class 에 대한 함수를 제공한다. 그러나 이것들을 사용하는 대신 one-vs-all 방법을 사용할 수도 있다. k 개의 클래스가 있다면 k 개의 SVM 훈련시키면 된다.

Logistic regression vs SVM

(http://blog.csdn.net/abcjennifer)

(1) n >= m 이면 logistic regression 이나 linear kernel 이 낫다.
(2) n 이 작고, m 이 중간 사이즈면 gaussian kernel 을
(3) n 이 작고 m 이 크면 gaussian 은 상당히 느려진다. feature 를 좀 수정하고, logistic 이나 linear kernel 을 이용한다.

SVM 의 장점은 다양한 kernel 을 non-linear function 을 훈련시키기 위해 사용할 수 있다는 점이다.

References

(1) Machine Learning by Andrew NG
(2) http://blog.csdn.net/linuxcumt
(3) http://blog.csdn.net/abcjennifer