ML 05: Back Propagation

지난시간엔 왜 neural network 를 사용하는지 알아보았다. 데이터의 차수가 매우 클 때 logistic regression 으로는 성능이 떨어지거나 overfitting 의 문제가 발생할 수 있다는 사실을 알게 되었고, 마지막엔 multi class 문제를 어떻게 해결할지도 잠깐 논의 해봤다.

이번에는 back propagation, gradient checking 에 대해서 배워보자.

Cost Function

시작하기 전에 몇 가지 표기법을 정의하자.

L 을 레이어의 수, s_l 을 해당 레이어의 유닛 수라 하자. 그러면 bianry classification 에서 S_L = 1 이다. 아웃풋 레이어의 유닛 수를 더 간단히 K 라 하자.

이제 neural network 에 대한 cost function 을 볼건데 먼저 binary classification 의 regularized cost function 식을 다시 보자.

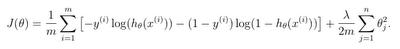
지난 시간에 언급했듯이 신경망에서 각 단계는 logistic regression 과 같이 때문에 L 의 신경망은 L-1 의 logistic regression 의 식으로 변환할 수 있다.

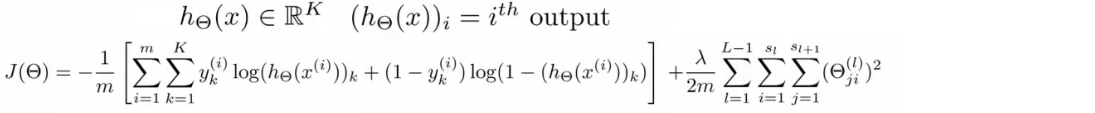
이 식의 가장 큰 문제점은 이 식을 보면 당황스럽다는 것이다.

뒷 부분 regularization term 은 이해하기 어렵지 않다. 신경망에선 weight (theta) 의 행렬이 이전 레이어와 다음 레이어의 유닛 수로 구성되므로 (theta_ji^l)^2 으로 모든 theta^2 를 구할 수 있다.

여기서 i = 1 부터 시작하는 이유는 logistic regression 의 regularization term 에서 theta_0 을 포함하지 않는것과 같다.

문제는 시그마 K 부분인데, K 가 이 신경망에서 클래스의 개수 라는 점을 고려하면 y_k 는 [0; 0; 1; 0; ...] 에서 k 번째 값, (h0)_k 또한 k 번째 output unit 의 값 이라 보면 된다.

원래 cost function 정의 자체가 우리가 가진 hypothesis 로 구한 값과 본래의 값 y 와의 차이를 알려주는 것이므로 K 개의 클래스가 있을때는 각 클래스 위치의 값과 본래의 k-dimensional vector y 값의 해당 포지션의 차이를 모두 합한 값을 구하는 것이라 neural network 의 cost function 정의할 수 있다.

Backpropagation: Algorithm

gradient computation 을 위해서는 cost function 과 각 l 의 i, j 위치의 theta 에 대해서 cost function 의 partial derivative 를 구해야 한다. 네?

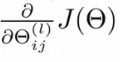
(http://www.holehouse.org/)

다음과 같은 신경망이 있다고 하자, 그리고 training set 이 (x, y) 만 있다고 한다면 cost function 을 얻기 위해 다음의 forward propagation 을 진행하면 된다.

(http://www.holehouse.org/)

그럼 i, j, l 에 대한 cost function 의 partial derivative 는 어떻게 구할까?

back propagation 을 이용하면 된다. 개요는 이렇다. 마지막 단계에서 신경망을 이용해 얻은 값 a4 와 실제 값인 y 의 차이를 d4(delta) 라 하자. 보면 알겠지만 이건 error 다. 이 에러값을 이용해 d3 즉 레이어 3 에서의 에러값을 구하고, 반복하면서 d2 까지 구한다. (d1 은 없다. a1 이 input 이기때문)

forward propagation 과 다르게 뒤에서 앞쪽으로 error 가 전파되기 때문에 back propagation, BP 라 부른다. BP 로 찾은 d 값을 이용하면 partial derivative 를 쉽게 구할 수 있다. d3, d2 를 구하는 방법은 아래와 같다.

(http://www.holehouse.org/)

식에 대한 intuition 은 이전 레이어의 유닛의 d 를 얻기 위해서 다음 레이어의 모든 d 와 theta 의 곱을 이용한다는 사실이다. 이건 FP 에서 다음 단계의 유닛 a 를 얻기 위해 이전 단계의 모든 유닛과 theta 를 이용한다는 사실을 거꾸로 생각해보면 이해할 수 있다.

이때 sigmoid function g 의 미분은 g' = g(1-g) 이고, g'(z3) 는 a3 * (1 - a3) 으로 고쳐쓸 수 있다.

만약에 regularization term 을 무시한다면 다시 말해 lambda = 0 이면, partial derivative 는 d 를 이용해 쉽게 작성할 수 있다.

알고리즘을 좀 자세히 살펴보면

(http://blog.csdn.net/abcjennifer)

지금까지의 설명과 같이 먼저 FP 를 진행해서 각 레이어의 유닛 a 을 구하고, BP 를 진행한다.

이 때 마지막 단계에서 삼각형(large delta, Delta) 에 이전 단계의 DELTA 와 aj^(l)di(l+1) 를 더하는데, 사실 aj^(l)di(l+1) 가 바로 reulgarization term 을 무시했을 때의 partial derivative 다.

이렇게 모든 DELTA 를 구하고 나서 이제 D 에 regularization term 을 추가한다.

(http://blog.csdn.net/abcjennifer)

이제 regularization term 까지 더한 D 가 바로 partial derivative 다. 너무 난해하다

Back propagation: Intuition

조금 더 Back propagation, BP 를 살펴보자. dj^(l-1) 를 얻기 위해 d^(l) 과 theta 를 이용한다는 사실은 알겠다. 근데 g' 이라던지 이런건 도대체 어디서 나온걸까?

처음으로 다시 돌아가면 cost function 에서 training set 이 1개라면 다시 말해 m=1 이고, lambda=0 이라면 cost function 은 h(x), y 에 의해 좌우된다. 결국 squared error 와 다를바 없다는 소리다.

(http://blog.csdn.net/linuxcumt)

결국 dj^(l) 은 aj^(l) 의 error of cost 다. 더 엄밀히 수학적으로 말하자면 dj^(l) 은 cost(i) 에 대한 zj^(l) 의 partial derivative 다. zj^(l) 이 변할때 i 에 대한 cost 가 얼마나 변하는지가 바로 d 란 이야기다.

(http://blog.csdn.net/linuxcumt)

d 에 대한 더 엄밀한 수학적 증명은

(http://blog.csdn.net/abcjennifer)

Unrolling Parameters

octave 에서 reshape 함수를 이용해서 벡터를 매트릭스로 변환하는 방법을 알려준다.

(http://blog.csdn.net/linuxcumt)

Gradient Checking

BP 를 이용해서 neural network 의 cost function 을 위한 partial derivative 를 구하는 방법을 배웠는데, 안타깝게도 이게 쉽게 구현할 수 있는것이 아니라서 버그가 생길 수 있다.

gradient checking 이란 방법을 이용하면 FP, BP 의 구현이 완벽함을 보일 수 있다. 배워보자.

(http://blog.csdn.net/linuxcumt)

말 그대로 기울기에 대한 근사치를 구해서 비교하여 검증하는 방법이다. e(엡실론) 이 매우 작다 하고, 0-e 와 0+e 두 점 사이의 기울기를 구해 gradient 와 근사한 값을 구한다.

우리는 0 가 하나가 아니기 때문에, 각각의 0(theta) 에 대해 모두 gradient 의 근사치를 구해야 한다.

(http://blog.csdn.net/linuxcumt)

마지막에서 gradient checking 을 이용해 구한 gradApprox 와 실제 *BP 를 이용해 구한 graident 인 Dvec 과 비슷한지 검사한다.

그러나, 한가지 알아야할 사실이 있다. gradient checking 은 굉장히 비싸기 때문에 Dvec 과 비슷한 값을 구했는지 검사한 후에는 gradient checking 를 꺼야한다.

(http://blog.csdn.net/linuxcumt)

Random Initialization

gradient desecnt 를 위한 함수를 사용할때 initialTheta 를 줘야한다. 그냥 zeros 로 만들까? neural network 에서 모든 theta 가 0 으로 시작하면 모든 유닛의 값이 같아진다. 오류(d) 도 같고, partial derivative 의 값도 같으므로 다음 이터레이션에서도 같은 유닛은 같은 값을 가지고 이게 반복된다.

결국 내가 가진 모든 히든 유닛이 같은 계산을 해 내고 있으므로, 하나의 feature 에 대한 극도로 중복된 연산을 볼 수 있다.

(http://blog.csdn.net/linuxcumt)

theta 가 대칭이기 때문에 발생하는 문제인데 symmetry breaking 을 위해 [-e, e] 사이의 theta 를 랜덤으로 골라보자. 물론 이 e 는 gradient checking 에서의 e 와 관련이 없다.

(http://blog.csdn.net/abcjennifer)

Putting It Toghther

(1) neural network 를 훈련시킬 때 먼저 해야 할 일은 아키텍쳐를 고르는 일이다.

output unit 과 input unit 은 class 와 feature 수로 결정된다. 문제는 hidden unit 과 hidden layer 의 수다.

기본적으로는 1개의 히든 레이어를 사용하거나, 1개 이상을 사용한다면 같은 수의 히든 유닛을 모든 히든 레이어에서 사용하는것이 대부분 계산 비용 면에서 낫다.

(http://blog.csdn.net/linuxcumt)

(2) weights 를 랜덤하게 초기화 한다.
(3) forward propagation
(4) cost function 을 구한다.
(5) partial derivatives 구하기 위해 back propagation

BP 를 할때는 traning set 의 수 m 번 만큼 루프를 돌면서 각 (xi, yi) 를 이용해 FP, BP 를 한다.

(http://blog.csdn.net/linuxcumt)

(6) gradient checking 을 이용해 얻은 근사치와 partial derivatives 를 비교한다. 값이 적당히 비슷하면 gradient checking 코드를 제거한다.
(7) cost function 을 최소화 하기 위해 gradient descent 나 advanced optimization method 를 사용한다.

한 가지 알아야 할 사실은 neural network 의 cost function 은 non-convex 이기 때문에 local optimum 에서 멈출 수 있다.

그런덷 문제가 굉장히 크다면 gradient descent 로 찾은 local optimum 도 충분히 좋은 값이라고 한다.

(http://blog.csdn.net/linuxcumt)

처음에 1장에서 봤던 언덕 그림이다.

(http://mapository.tistory.com/59)

여기서 gradient descent 가 하는 일은 언덕을 내려가는거고, back propagation 이 하는 일은 방향을 잡아주는 일이다.(z 가 변했을 때 cost function 값이 변하는 양인 오차 d 의 값이 적어지도록 방향을 잡아줌)

그래서 신경망에서 gradient descent 를 사용한다 하더라도 적당히 좋은 로컬 옵티멈을 찾아준다는 훈훈한 이야기

Autonomous Driving

무인 운전을 신경망으로 어떻게 해결하는지를 보여준다. 미리 사람이 한번 운전한 경로(y) 를 바탕으로 학습하는데, 생각도 못해본 분야들에 이미 이런 기술들이 적용되어 있구나 싶다. 무려 1992년에 했던 실험이다

References

(1) http://aimotion.blogspot.kr/
(2) http://www.holehouse.org/mlclass/
(3) http://blog.csdn.net/abcjennifer/
(4) http://blog.csdn.net/linuxcumt