ML 04: Neural Network
지난 시간에는 실리콘 밸리의 머신러닝 개발자들이 귀한대접을 받는다는 훈훈한 덕담으로 강의가 끝났다. 이번시간에는 뜬금없이 Neural Network (신경망) 을 건들다가 놀랍게도 그것이 logistic regression 과 연관이 있으며 n 이 매우 클 경우의 classification 문제를 해결할 수 있다는 것을 배운다.
Non-Linear Hypotheses
다음과 같은 트레이닝 셋이 있을때, 두 집단을 classification 하는 hypothesis 를 찾는다고 하자.
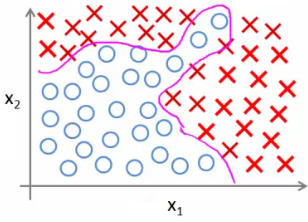
x1 과 x2 만으로는 찾을 수 없으니, 더 많은 feature x1^2, x1x2, x2^2 를 도입한다 하자. 트레이닝 셋에 적합한 가설을 찾을수는 있겠지만, 항상 좋은건 아니다.
(1) 우선 지난 시간에 언급했듯이 Overfitting 이 발생할 수 있고
(2) feature 수가 n 이라 할때, 모든 quadratic feature 를 도입하면 feature 수가 O(n^2) (n^2/2)만큼 늘어난다. (아래 그림 참조) 다시 말해서 계산 비용이 엄청나게 비싸진다.

(http://blog.csdn.net/feliciafay)
그리고 feature 수를 줄이기 위해 x1^2, x2^2, x3^2 ... 등 quadratic feature 만을 도입하고 나머지 parameter 를 버리면, hypothesis 가 underfit 할 수 있다.
만약 feature 를 cubic 까지 도입하면 feature 수가 O(n^3) 으로 늘어나 계산시간은 어마어마하게 걸린다. 따라서 차수를 늘려 문제를 해결하려는 방법은 n 이 클때 좋은 방법이 아니다. 게다가 일반적으로 대부분의 문제들은 n 이 큰편이다.
자동차 이미지 인식 문제를 고려해 보자. 이미지는 픽셀이므로, 50 * 50 픽셀로 구성된 경우 n = 2500 이다.

(http://blog.csdn.net/feliciafay)
이건 그레이스케일의 경우고 만약 RGB 라면 여기에 3을 곱해서 n = 7500 이 된다. quadratic 이면 7500^2 / 2, 대략 3 millions 개의 feature 를 가지게 된다. 이쯤되면 답이 없다. n 이 큰 classification 에 대해 사용할 수 있는 다른 방법은 없을까?
Model Representation
잠깐 눈을 돌려 Neural Networks 에 대해 이야기 해 보자. 다양한 알고리즘을 개발하는 대신 스스로 학습하는 뇌를 모방한 알고리즘을 개발할 수 있다면 진짜 AI 를 구현할 수 있지 않을까? 라는 질문에서 Neural networks 는 출발한다.
뇌를 모방한 알고리즘을 만들려면, 인간의 뇌가 어떻게 작동하는지 알아야한다. 뇌는 Neuron 이라는 단위의 집합으로 구성되었는데, 요로코롬 생겼다.
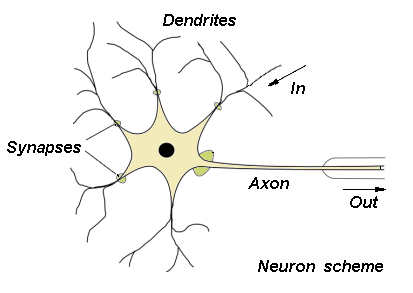
(http://home.agh.edu.pl/~vlsi/AI/intro/)
여기서 Dendrite 라는 부분이 input 이고, Axon 이 output 이다. 이걸 모델링하면,

(http://blog.csdn.net/feliciafay)
위 그림에서 좌측에 있는 x1, x2, x3 가 input 이라 보면 되고, h0(x) 는 이전처럼 0^T * x 에 sigmoid function 을 적용한 것이다. 그리고 neural network 에서 parameter 대신 0(theta) 를 weights 라 부르기도 한다. x0 은 값이 1 이고, bias unit 이라 부르는데 편의상 그리기도 하고 안그리기도 한다. 교수님 뜻대로 하소서
여기까지는 단일 neuron 을 모델링 한것이고, neural network 는 여러개의 neuron 들이 합쳐진 것이다. 간단히 그려보면,

(http://blog.csdn.net/feliciafay)
여기서 layer 1 은 input layer, 마지막인 *layer 3*은 output layer 다. 그리고 가운데 있는 레이어들, 여기서는 layer2, hidden layer 라 부른다. 디버깅이 아니라면 hidden layer 에서 산출되는 값들을 관측하려고 할 필요는 없다. hidden layer 는 하나 이상일 수 있다. 실제 계산 과정을 보면

(http://blog.csdn.net/feliciafay)
ai^j 는, j 번째 hidden layer 에서 i 번째 unit 이다. 0(theta)^j 는 layer j 와 layer j+1 사이에서 사용되는 weights 다. 이때 hidden layer 의 각 unit 마다 input 을 위한 weight 를 가지고 있다고 하면 위의 그림에서 0 의 dimension 은 3 * 4 다. (bias unit x0 포함)
If network has
s_junits in layerj,s_j+1units in layerj+1, then0^jwill be dimensions_j+1 * (s_j + 1)
이제 output layer 를 잘 보면 이 레이어의 input 은 a^(2) 고, weight 로 0^2 를 가지고 있다. 따라서 h0(x) 는 위의 식처럼 된다.
Forward Propagation
위 그림처럼 x 를 받아, h0(x) 를 계산하는 방법을 forward propagation 이라 부르는데 vectorization 을 이용해서 간단히 해 보자.

(http://www.try2go.com/201408/neural-networks-1/)
sigmoid fucntion g 내부의 수식을 z 라 부르고 a^(1) = x 라 두면, 우측처럼 수식이 심플해진다. z^(2) = 0^(1) * a^(1) 이고, 여기에 sigmoid function 을 적용하면 a^(2) 가 나온다. 여기에 bias unit a_0^(2) = 1 을 더해 a^(2) 를 4차원 벡터로 만들면 다시 z^(3) 를 계산할 수 있다.
자, 이제 왜 neural network 를 뜬금없이 공부하다가 forward propagation 의 vectorization 까지 고려했는지를 밝힐 시간이다! 위 그림에서 a^(1) 즉, layer 1 을 가려버리면 아래와 같은데

(http://www.try2go.com/201408/neural-networks-1/)
이때 h0(x) 를 계산하는 식을 구해보면, logistic regression 과 똑같다. 오오 머신러닝 오오
결국, neural network 가 하는 일은 logistic regression 이다. 단지 hidden layer 에서 x1, x2, x3 를 적당한 weight 로 훈련시켜 새로운 feature a1^(2), a2^(2), a3^(2) 를 만들어 내고, 그걸로 logistic regression 을 할 뿐이다.
다시 한번 정리하자면 neural network 는 feature 를 훈련시켜 다른 값을 가진 feature 로 바꾸는 과정을 통해 hypothesis 를 매우 고차의 다항식으로 만들지 않고도 n 이 매우 큰 경우의 classification 을 풀 수 있도록 한다. 항상 같은 개수의 feature 만 나오는건 아니고, 더 줄이거나 좀 더 늘릴 수도 있다. 아래의 그림을 보자.

(http://alphaism.wordpress.com/)
Examples
먼저 간단히 AND 연산을 neural network 로 구현한다 하자.

(http://www.try2go.com/201408/neural-networks-1/)
위 그림처럼 z^(2) = -30 + 20x1 + 20x2 라면, 우측 표 처럼 각각 h0(x) 값이 나오고, sigmoid function 은 4.6 정도일때 y ~= 0.99 이므로 g(+10) 은 거의 1, g(-10) 은 거의 0 이라 볼 수 있다.
XNOR 은 AND ~ AND ~ 그리고 OR 을 조합하면 만들 수 있다. 아래 그림을 보자.
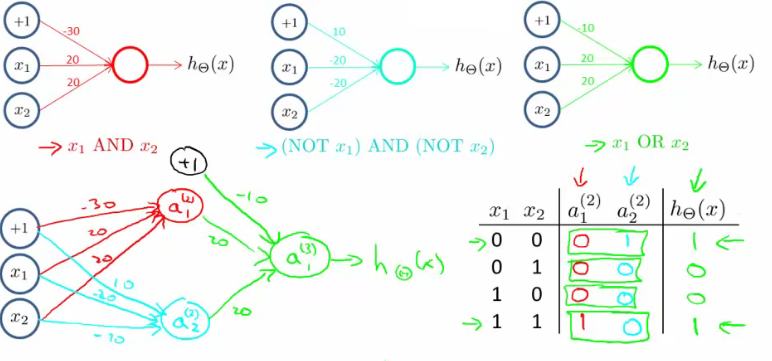
결국 neural network 는 각 hidden layer 에서 함수를 이용해 이전 단계의 결과에 어떤 처리를 가해 복잡한 일들을 해낼 수 있는 것이다.
Multiclass Classification
이제 multi-class 를 고려해 보자.

(http://www.try2go.com/201408/neural-networks-1/)
위 그림처럼 4개의 클래스가 있을 때, output 인 h(x) 를 4 * 1 vector 로 만들도록 하고, 각 클래스에 대해서 [1; 0; 0; 0], [0; 1; 0; 0], [0; 0; 1; 0], [0; 0; 0; 1] 이 되도록 훈련시키면 된다. 기본적인 아이디어는 one vs all method 와 같다.
References
(1) http://blog.csdn.net/feliciafay
(2) http://www.holehouse.org
(3) http://home.agh.edu.pl/~vlsi/AI/intro/
(4) http://www.try2go.com/201408/neural-networks-1/
(5) http://alphaism.wordpress.com/
comments powered by Disqus