Intro to Data Science 3
Optimization Problems
일반적으로 최적화 문제는 크게 두 파트로 구성된다.
- An objective funciton that is to be maximized or minimized
- A set of constraint (possibly empty) that must be honored
최적화 문제의 예로는
- Shortest path
- Traveling salesman
- Bin packaing
- Sequence alignment
- Knapsack
이런 알려진 문제들을 공부함으로써 problem reduction 을 이용할 수 있다.
Knapsack Problem
먼저 greedy approach 를 사용해 보자. 이 방법을 적용하기 위해서는 무엇이 best 인지 정해야 한다. value 가 높은것이나, value/weight 가 높은것 등 다양한 기준을 세울 수 있다.
문제를 모델링 해보자. 아이템부터
class Item(object):
def __init__(self, n, v, w):
self.name = n
self.value = v
self.weight = w
def getName(self):
return self.name
def getValue(self):
return self.value
def getWeight(self):
return self.weight
def __str__(self):
result = '<' + self.name + ', ' + str(self.value)\
+ ", " + str(self.weight) + '>'
return result
def buildItems():
names = ['clock', 'painting', 'radio',
'vase', 'book', 'computer']
vals = [175, 90, 20, 50, 10, 200]
weights = [10, 9, 4, 2, 1, 20]
Items = []
for i in range(len(vals)):
Items.append(Item(names[i], vals[i], weights[i]))
return Items
greedy algorithm 을 구현하면
def greedy(Items, maxWeight, predicate):
assert type(Items) == list and maxWeight >= 0
orderedItems = sorted(Items, key=predicate, reverse=True)
result = []
totalVal = 0.0
totalWeight = 0.0
i = 0
while totalWeight < maxWeight and i < len(Items):
if (totalWeight + orderedItems[i].getWeight()) <= maxWeight:
result.append(orderedItems[i])
totalWeight += orderedItems[i].getWeight()
totalVal += orderedItems[i].getValue()
i += 1
return (result, totalVal)
# predicate
def value(item):
return item.getValue()
def weightInverse(item):
return 1.0 / item.getWeight()
def density(item):
predicate 를 받아, 이 순서대로 items 를 정렬 한 뒤 반복문을 돌면서 아이템을 집어넣는다. sorted 함수는 predicate 에 따라 정렬 한 뒤 새로운 리스트를 생성한다.
orderedItems = sorted(Items, key=predicate, reverse=True)
이제 테스트 코드를 작성하자.
# test
def testGreedy(Items, constraint, pred):
items, val = greedy(Items, constraint, pred)
print ('Total value of items taken = ' + str(val))
for item in items:
print ' ', item
def simulation():
maxWeight = 20
Items = buildItems()
print ('Items to choose from')
for item in Items:
print ' ', item
print 'by value'
testGreedy(Items, maxWeight, value)
print 'by 1 / weight'
testGreedy(Items, maxWeight, weightInverse)
print 'by density'
testGreedy(Items, maxWeight, density)
simulation()
결과는
Items to choose from
<clock, 175, 10>
<painting, 90, 9>
<radio, 20, 4>
<vase, 50, 2>
<book, 10, 1>
<computer, 200, 20>
by value
Total value of items taken = 200.0
<computer, 200, 20>
by 1 / weight
Total value of items taken = 170.0
<book, 10, 1>
<vase, 50, 2>
<radio, 20, 4>
<painting, 90, 9>
by density
Total value of items taken = 255.0
<vase, 50, 2>
<clock, 175, 10>
<book, 10, 1>
<radio, 20, 4>
보면 알겠지만 탐욕적으로 접근했을때 항상 최적의 답안을 찾으리라는 보장이 없다. 패가망신
전체적인 성능은 sorted + while 에서, O(n logn) 이다. (n 은 아이템 갯수)
0/1 Knapsack Problem
greedy 는 최적의 답을 제공해 주지 않는다. 어떻게 해야할까? 한가지 방법은,
벡터 L 을 각 아이템의 가중치로 채우고, 벡터 V 를 각 아이템이 선택되었는지, 선택되지 않았는지를 1/0 으로 표시 한 뒤 V * L 이 최대가 되는 V 를 찾으면 된다. 물론 이 값은 무게의 최대치인 W 를 넘을 수 없다.
그럼 이제 문제는 다양한 종류의 V 를 만드는 문제로 치환된다. 일반적으로는 V 의 수는 2^n 이겠지만, 여기서는 W 란 제약조건이 있으므로 그것보다는 작은 수가 될 것이다.
넘어가기 전에 잠깐! 수의 크기에 대해 감을 잡고 넘어가자. 요즘 CPU 는 1GHz 는 그냥 넘으니까, 1초의 10억번이 넘는 연산을 할 수 있다. 한 작업에 대해 수백개의 명령이 필요하므로, 1초에 수백만의 작업을 할 수 있다.
수백만은 얼마나 큰 수일까? 10! = 3628800 이다. 대략 11 ~ 10 개를 배열해도 백만가지의 순열이 만들어진다. 그리고 2^20 = 1048576 이므로 원소가 스무개인 집합의 부분집합이 백만개정도라 보면 된다.
따라서 최적해를 찾고자 할때는 10!, 2^22 정도가 몇초 내외의 감당할만한 계산시간이라 볼 수 있다.
Brute Force Approach
power set 을 만들어 보자.
# brute force
def int2bin(n, digit):
assert type(n) == int and type(digit) == int
assert n >= 0 and n < 2 ** digit
# binary string
binStr = ''
while n > 0:
binStr = str(n % 2) + binStr
n = n // 2
while digit - len(binStr) > 0:
binStr = '0' + binStr
return binStr
def powerSets(Items):
count = 2 ** len(Items)
binStrs = []
for i in range(count):
binStrs.append(int2bin(i, len(Items)))
powerSet = []
for bs in binStrs:
elem = []
for i in range(len(bs)):
if bs[i] == '1':
elem.append(Items[i])
powerSet.append(elem)
return powerSet
이제 테스트 함수를 작성하자.
def optimalItems(powerSet, constraint, getValue, getWeight):
optimalSet = None
optimalValue = 0.0
for Items in powerSet:
ItemsValue = 0.0
ItemsWeight = 0.0
for item in Items:
ItemsValue += getValue(item)
ItemsWeight += getWeight(item)
if ItemsWeight <= constraint and ItemsValue > optimalValue:
optimalValue = ItemsValue
optimalSet = Items
return (optimalSet, optimalValue)
def bruteForceSolution():
Items = buildItems()
pset = buildPowerSet(Items)
items, value = optimalItems(pset, 20,
Item.getValue,
Item.getWeight)
print ('brute force : ' + str(value))
for item in items:
print ' ', item
돌려보면
bruteForceSolution()
brute force : 275.0
<clock, 175, 10>
<painting, 90, 9>
<book, 10, 1>
다 좋은데, 아이템의 개수가 많아지면 2^n 으로 숫자가 커지므로 계산 비용이 어마어마하게 커진다. 다른 방법을 찾아보자.
Decision Tree
트리의 각 depth 를 아이템으로 표현하고, left node 를 1 (selected), right node 를 0 (unselected) 로 정해 각 노드마다 전체 value, weight 를 기록하도록 하면 search space 를 상당히 줄일 수 있다. 왜냐하면 특정 아이템을 선택 한 후 무게를 초과하면, 그 하위 트리는 살펴보지 않아도 되기 때문이다.
이 트리를 decision tree 라 부른다.
# decision tree
def maxVal(items, avail):
if items == [] or avail == 0:
result = (0, ())
elif items[0].getWeight() > avail:
# do not take
result = maxVal(items[1:], avail)
else:
current = items[0]
# left branch : take the item
leftValue, leftItems = maxVal(items[1:],
avail - current.getWeight())
leftValue += current.getValue()
# right branch : do not take the item
rightValue, rightItems = maxVal(items[1:],
avail)
if leftValue > rightValue:
result = (leftValue, leftItems + (current,))
else:
result = (rightValue, rightItems)
return result
def decisionTreeSolution():
Items = buildItems()
value, selected = maxVal(Items, 20)
for item in selected:
print item
print ('decisition tree value : ' + str(value))
실행하면
# decisionTreeSolution()
<book, 10, 1>
<painting, 90, 9>
<clock, 175, 10>
decisition tree value : 275
모든 power set 을 살펴보지 않는다는 점에서 맘에 들지만, 가방의 용량이 상당히 크다면 power set 처럼 2^n 으로 증가할 수 있다.
Trade Off
greedy 는 매 선택마다 최선을 택함으로써 locally optimal 을 찾지만 이게 global optimal 을 의미하진 않는다. 대신, 상당히 납득할만한 답안을 빠른 시간 안에 줄 수 있다.
Memoization
decision 트리를 잘 보면 sub-problem 에서 같은 계산을 여러번 하는걸 볼 수 있다. 예를 들어 {a, b, c, d} 의 아이템이 있을때 {a, c, d} 와 {b, c, d} 는 다른 분기인데, 둘 다 {c, d} 를 계산하고 있다.
이 문제는 피보나치에서도 발견할 수 있는데,
def fib(n):
assert type(n) == int and n >= 0
if n == 0 or n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
fib(n-1) 에서 fib(n-2) 를 계산하니까, fib(n-2) 를 두번 계산하는 셈이다.

(https://www.cs.cmu.edu/~adamchik)
한번 계산한 결과는 저장해 놓고 다음에 쓰는 memoization 을 이용해 보자.
Memoization: the first time we compute a function, keep track of the value; any subsequent time, just look up the value
def fastFib(n, memo):
assert type(n) == int and n >= 0
if n == 0 or n == 1:
return 1
if n in memo:
return memo[n]
result = fastFib(n-1, memo) + fastFib(n-2, memo)
memo[n] = result
return result
def testFastFib(n):
assert type(n) == int and n >= 0
for i in range(n):
print ('fast fib of', i, '=', fastFib(i, {}))
memoization 은 dynamic programming 등에 사용할 수 있다.
Graph
optimization problem 은 search problem 이라 볼 수 있다. 다양한 탐색 공간 속에서 최적의 답을 검색해 나가는 문제와 동일하기 때문이다.
그래프를 모델링 해 보자.
class Node(object):
def __init__(self, name):
self.name = str(name)
def getName(self):
return self.name
def __str__(self):
return self.name
class Edge(object):
def __init__(self, src, dest):
self.src = src
self.dest = dest
def getSrc(self):
return self.src
def getDest(self):
return self.dest
def __str__(self):
return str(self.src) + ' -> ' + str(self.dest)
class WeightedEdge(Edge):
def __init__(self, src, dest, weight=1.0):
self.src = src
self.dest = dest
self.weight = weight
def getWeight(self):
return self.weight
def __str__(self):
return str(self.src) + ' -> ('\
+ str(self.weight) + ')'\
+ str(self.dest)
class Digraph(object):
def __init__(self):
self.nodes = set([])
self.edges = {}
def addNode(self, node):
if node in self.nodes:
raise ValueError('duplicated node')
else:
self.nodes.add(node)
self.edges[node] = []
def addEdge(self, edge):
src = edge.getSrc()
dest = edge.getDest()
if not(src in self.nodes and dest in self.nodes):
raise ValueError('unknown node')
self.edges[src].append(dest)
def childrenOf(self, node):
return self.edges[node]
def hasNode(self, node):
return node in self.nodes
def __str__(self):
res = ''
for src in self.edges:
for dest in self.edges[src]:
res = res + str(src) + ' -> ' + str(dest) + '\n'
return res[:-1]
# undirected
class Graph(Digraph):
def addEdge(self, edge):
Digraph.addEdge(self, edge)
rev = Edge(edge.getDest(), edge.getSrc())
Digraph.addEdge(self, rev)
그래프 최적화 문제의 예는
- Shortest path
- Shortest weighted path
- Cliques
- Min cut
이제 테스트 그래프를 만들어 보자.
def makeEdge(nodes, src, dest):
return Edge(nodes[src], nodes[dest])
def testGraph():
nodes = []
# index will be the name of each node
for idx in range(6):
nodes.append(Node(idx))
g = Digraph()
for n in nodes:
g.addNode(n)
srcs = [0, 1, 2, 2, 3, 3, 0, 1, 3, 4]
dests = [1, 2, 3, 4, 4, 5, 2, 0, 1, 0]
for (s, d) in zip(srcs, dests):
g.addEdge(makeEdge(nodes, s, d))
print g
실행하면 이런 그래프를 얻을 수 있다.
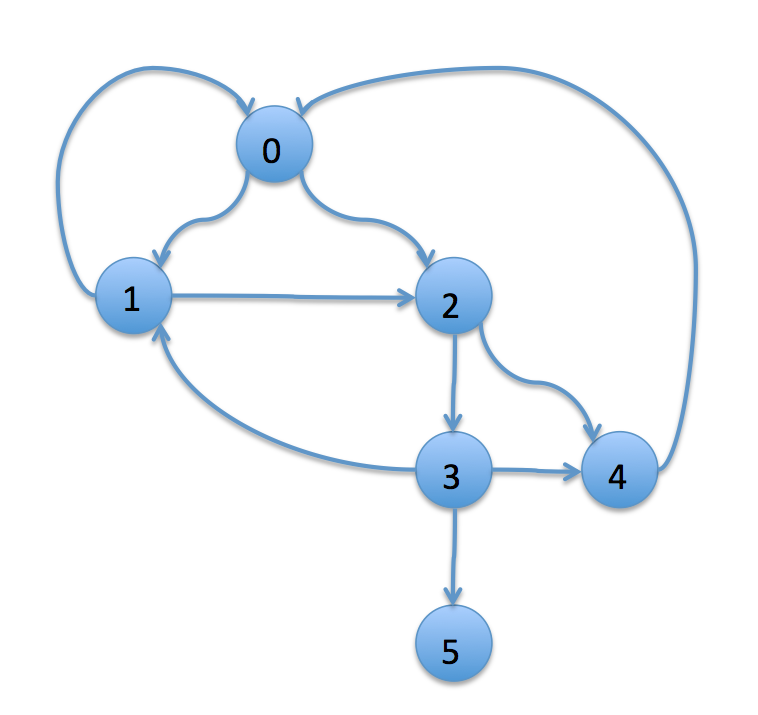
testGraph()
0 -> 1
0 -> 2
1 -> 2
1 -> 0
2 -> 3
2 -> 4
3 -> 4
3 -> 5
3 -> 1
4 -> 0
DFS
# assumes graph is a directed graph
def DFS(graph, start, end, path=[]):
path = path + [start]
if start == end:
return path
for node in graph.childrenOf(start):
if node not in path:
newPath = DFS(graph, node, end, path)
if newPath is not None:
return newPath
테스트 코드를 돌려보면 알겠지만, 최단경로를 돌려주진 않는다.
def makeEdge(nodes, src, dest):
return Edge(nodes[src], nodes[dest])
def testGraph():
nodes = []
# index will be the name of each node
for idx in range(6):
nodes.append(Node(str(idx)))
g = Digraph()
for n in nodes:
g.addNode(n)
srcs = [0, 1, 2, 2, 3, 3, 0, 1, 3, 4]
dests = [1, 2, 3, 4, 4, 5, 2, 0, 1, 0]
for (s, d) in zip(srcs, dests):
g.addEdge(makeEdge(nodes, s, d))
return g, nodes
def visit():
g, nodes = testGraph()
path = DFS(g, nodes[0], nodes[5], [])
for p in path:
print p
visit()
0
1
2
3
5
처음 찾은 목적지까지의 거리보다 더 짧은 목적지까지의 거리만을 탐색하는 알고리즘을 고려해보자. 가장 먼저 찾은 목적지까지거리를 shortest 에 저장하고, 이것보다 짧은 경로만 탐색한다.
# assumes graph is a directed graph
def shortestDFS(graph, start, end, path=[], shortest=None):
path = path + [start]
if start == end:
return path
for node in graph.childrenOf(start):
if node not in path:
if shortest is None or len(path) < len(shortest):
newPath = shortestDFS(graph, node, end, path, shortest)
if newPath is not None:
shortest = newPath
return shortest
이부분이 핵심이다
if shortest is None or len(path) < len(shortest):
실제로 돌려보면 0, 2, 3, 5 로 최단경로를 돌려준다.
Clique
각 점이 나머지 모든 점과 연결된 그래프를 clique 라 부르는데, 재미난 특징이 몇 개 있다.
(1) 모든 edge 의 수는 n * (n - 1) / 2 다.
(2) 임의의 두 점 A, B 에 대해 길이가 1 <= m <= (n-1) 인 모든 경로는 (n-2)! / (n-m-1)! 이다.
(3) (2) 를 이용하면, 모든 경로를 탐색할 경우의 퍼포먼스는 O((n-2)!) 이다. 여기서 1/0! + 1/1! + 1/2! ... + 1/n! <= e, e 는 상수
BFS
def BFS(graph, start, end, q=[]):
init = [start]
q.append(init)
while len(q) != 0:
# get a path from q
current = q.pop(0)
lastNode = current[len(current) - 1]
if lastNode == end:
return current
for nextNode in graph.childrenOf(lastNode):
if nextNode not in current:
path = current + [nextNode]
q.append(path)
return None
References
(1) MIT 6.00.2 2x in edx
(2) https://www.cs.cmu.edu/
comments powered by Disqus