Data Analysis Intro to Data Science 1

Intro to Data Science 1

Simulation Models

Simulation attempts to build an experimental device called model

Simulation model is descriptive, not prescriptive

직역하자면 시뮬레이션은 실험가능한 도구인 모델을 만들어낸다. 모든 모델이 정확하진 않지만, 다시 말해 현상을 완벽하게 설명하진 못하지만, 어떤 모델들은 대략 비슷하게 사실을 예측해 낸다. 그런점에서 모델은 유용하다.

(1) Deterministic simulations are completely defined by the model rerunning the simulation will not change the result
(2) Stochastic simulations include randomness. Difference runs can generate different results

Nondeterminism

*Casual nondeterminism: * Not every event is caused by previous events

*Predictive nondeterminism: * Lack of knowledge about the world makes it impossible make accurate predictions about future states

*Stachastic Processes: * An ongoing process where the next state might depend on both the previous states and some random element

def rollDie():
   """returns an int between 1 and 6"""
   
def rollDie():
   """returns a random int between 1 and 6 """

위쪽 rollDie 는 underdetermined 인 반면 아래쪽은 non-deterministric

Hash Table

Many to One 이기 때문에 Collision 이 생긴다. bucket 을 이용해서 같은 키값을 가진 것들을 같은 버켓에 저장하도록 하면 충돌을 어느정도는 예방할 수 있다.

물론, 테이블이 커지면 충돌이 적어지고 탐색시간이 빨라지지만 메모리가 많이 들고, 테이블이 작아지면 충돌이 많아지고 탐색시간이 linear search 에 가깝게 느려지지만 메모리는 적게든다. Time / Space trade off

그리고 좋은 해쉬 함수는 uniform distribution 을 생성한다. 다시 말해서 모든 버킷은 같은 수의 데이터를 담고 있어야 한다.

해시 테이블은 time / space trade off 를 극명하게 보여주는데, collision 이 하나도 없을 때 개당 1 byte 인 10^9 개의 원소를 담고자 한다면, 1GB 가 필요하다.

그래서 해시 테이블을 만들 때는 가능한한 메모리가 허락하는 한도 내에서 최적화 할 필요가 있다. 다시 말하면 table size 와 lookup time 을 동시에 고려해야 한다는 뜻이다.

버킷 내부에 a 개를 저장하면 원소를 검색하는데 O(a) 시간이 걸리지만 메모리는 1/a 배 만큼 줄어든다.

이제 해쉬 함수의 성능을 적어도 한번 충돌이 일어날 수 있는 확률 로 표현해 보자. 한번도 충돌이 나지 않을 경우를 1 에서 빼면 된다.

입력 원소 K 개에 대해, 해쉬함수가 range(n) 의 uniform distribution 을 만들때 hash(k) = 1/n 이다. 이 때 충돌이 한번도 일어나지 않을 확률은 1 * (n-1)/n * (n-2)/n * .. (n-(k-1))/n 이다. 이 값을 1에서 빼면 *적어도 한번 충돌이 일어날 수 있는 확률*을 구할수 있다.

Birthday Attack

일년이 365일 이라 하면, 얼핏 생각하기에 365명 정도는 모여야 생일이 같은 사람 있을 것 같은데 사실 그렇지 않다. 실제로는 23명만 모여도 생일이 같은 두사람이 있을 확률이 50%를 넘고, 57명이 모이면 99%를 넘는다.

생일이 같은 두 사람을 찾는 것과 비슷하게, 암호학적 해시 결과가 같은 두 입력값을 자는 것 역시 모든 입력값을 계산하지 않앋 충분히 높은 확률로 해시 충돌을 찾을 수 있다. 이러한 암호 공격을 birthday attack 이라 부른다.

바꿔 말하면 birth day problem 은 해시 버켓이 365개인 해시 테이블이라 봐도 무방하다.

atLeastTwoSameBirthday 함수는 n + 1 명이 있는 방 안에서 적어도 두명은 생일이 같을 확률을, minNumOfPeopleProb 는 인자로 받은 p 보다 큰, 생일이 같을 확률을 얻기 위한 최소한의 인원을 돌려준다.

import operator


def atLeastTwoSameBirthday(n):
    xs = range(365 - n, 365)
    ys = map((lambda x: float(x) / 365), xs)
    return 1 - reduce(operator.mul, ys)


def minNumOfPeopleProb(p):
    for n in range(1, 365):
        if atLeastTwoSameBirthday(n) >= p:
            return n

    return n


print atLeastTwoSameBirthday(29)
print atLeastTwoSameBirthday(249)
print minNumOfPeopleProb(0.99)

Low of Large Numbers

In repeated independent tests with the same actual probabilty p of a particular outcome in each test, the chance of that the fraction of times that outcome occurs differs from p converges to zero as the number of trials goes to infinity

low of large numbers 는 |head - tail| 이 0에 수렴한다 를 의미하지 않는다. 오히려 |head - tail| 는 특정 비율이다(ratio)

이제 실제로 그러한지 시뮬레이션을 하기 위해 코드를 작성하면

import pylab
import random


def flipPlot(minExp, maxExp):
    ratios = []
    diffs = []
    xAxis = []

    for exp in range(minExp, maxExp + 1):
        xAxis.append(2 ** exp)

    for flips in xAxis:
        heads = 0
        for n in range(flips):
            if random.random() < 0.5:
                heads += 1

        tails = flips - heads
        ratios.append(heads / float(tails))
        diffs.append(abs(heads - tails))

    pylab.title('Diff between Heads and Tails')
    pylab.xlabel("# of Flips")
    pylab.ylabel("Abs(#Heads - #Tails)")
    pylab.plot(xAxis, diffs)
    pylab.figure()
    pylab.title("Heads / Tails Ratios")
    pylab.xlabel("# of Flips")
    pylab.ylabel("Heads / Tails")
    pylab.plot(xAxis, ratios)

random.seed(0)
flipPlot(4, 20)
pylab.show()

돌려서 나온 |head - tail| 의 그래프에서 선형 관계가 있다고 느낄 수 있는데 사실이 아니다. 우리는 x 축 값을 지수로 증가시켰기 때문에 우측에는 데이터가 별로 없는 반면 왼쪽에는 압축되어있다.

선 대신에 점 형태로 그래프를 그리고 축에 로그를 씌우는 코드로 바꾸자.

    #...
    
    pylab.title('Diff between Heads and Tails')
    pylab.xlabel("# of Flips")
    pylab.ylabel('Abs(#Heads - #Tails)')
    pylab.plot(xAxis, diffs, 'bo')
    pylab.semilogx()
    pylab.semilogy()
    pylab.figure()
    pylab.title('Heads / Tails Ratios')
    pylab.xlabel('# of Flips')
    pylab.ylabel('Heads / Tails')
    pylab.semilogx()
    pylab.plot(xAxis, ratios, 'ro')
    
    #...

heads / tails 는 1에 수렴하는걸 알 수 있다. 반면 |heads - tails| 는 완벽하진 않지만 선형의 그래프를 그리는걸 알 수 있다.

여기서 한 가지 사실을 알 수 있다.

Never possible to be assured of perfec accuracy through samplings, unless you sample the entire population

그렇다면 sample 에 대한 경향이 참일때, population 에 대한 경향이 참임을 증명하기 위해서 얼마나 많은 sample 을 살펴봐야 할까?

Depends upon the variance in the underlying distribution

물론 우리는 distribution 을 볼 수 없다. 샘플만 가지고 있기 때문에. 그럼 샘플로 variance 를 얻어보자.

We measure the amount of variance in the outcomes of multiple trials

standard deviation 을 이용하자. 표준편차는 우리가 가진 샘플이 평균에 모여있는지, 아닌지를 알려주는 지표다.

다시 말해서 standard deviation 이 작으면, 그래서 샘플의 평균에 샘플들이 대부분 모여있다는걸 알 수 있다면 작은 샘플에 대해서 얻은 어떤 경향이 population 에도 적용된다는 걸 알 수 있다.

def flipPlot(minExp, maxExp, trials):
    meanRatios = []
    meanDiffs = []
    sdRatios = []
    sdDiffs = []
    xAxis = []

    for exp in range(minExp, maxExp + 1):
        xAxis.append(2 ** exp)

    for flips in xAxis:
        ratios = []
        diffs = []

        for t in range(trials):
            heads, tails = runTrial(flips)
            ratios.append(heads / float(tails))
            diffs.append(abs(heads - tails))
        meanRatios.append(sum(ratios) / trials)
        meanDiffs.append(sum(diffs) / trials)
        sdRatios.append(stdDev(ratios))
        sdDiffs.append(stdDev(diffs))

    pylab.title('Mean of Diff bet Heads and Tails ('+str(trials)+' Trials)')
    pylab.xlabel("# of Flips")
    pylab.ylabel('mean Abs(#Heads - #Tails)')
    pylab.plot(xAxis, meanDiffs, 'bo')
    pylab.semilogx()
    pylab.semilogy()

    pylab.figure()
    pylab.title('SD of Diff bet Heads and Tails ('+str(trials)+' Trials)')
    pylab.xlabel('# of Flips')
    pylab.ylabel('SD Abs(#Heads - #Tails)')
    pylab.plot(xAxis, sdDiffs, 'bo')
    pylab.semilogx()
    pylab.semilogy()

    pylab.figure()
    pylab.title('Mean Heads / Tails Ratios')
    pylab.xlabel('# of Flips')
    pylab.ylabel('mean Heads / Tails')
    pylab.semilogx()
    pylab.plot(xAxis, meanRatios, 'ro')

    pylab.figure()
    pylab.title('SD Heads / Tails Ratios')
    pylab.xlabel('# of Flips')
    pylab.ylabel('SD Heads / Tails')
    pylab.semilogx()
    pylab.semilogy()
    pylab.plot(xAxis, sdRatios, 'ro')

random.seed(0)
flipPlot(4, 20, 20)
pylab.show()

이제 코드를 돌려보면, heads / tails 의 평균은 1로 수렴하는 것을, 표준편차는 n 이 커질수록 급격히 0 에 가까워지는걸 알 수 있다.

반면 |heads - tails| 의 평균은 n 이 증가할수록 여전히 커지고, 표준편차도 증가한다.

그럼, n 이 클수록 |heads - tails| 의 표준편차가 증가하므로 우리가 얻은 어떤 경향성이 n 이 클수록 더 믿지 못한다는 뜻일까?.

당연히 그렇지 않다! 표준편차는 그 자체로만 보아서는 안되고 평균과 연관지어 생각해야 한다. 평균이 100억일때, 표준편차가 100이라면 그건 데이터가 모여있음을 의미한다.

결국 평균 이 매우 달라지는 테스트를 할 경우엔 표준편차 를 사용하는건 적절하지 못하다는 사실을 알 수 있다.

coefficient of variation

그럼 평균이 달라지는경우 표준편차가 의미가 없다면, 어떤 값을 사용해야 population 의 variance 를 알 수 있을까? 표준편차를 평균으로 나눈 coefficient of variance 를 이용하면 된다. 일반적으로 이 값이 1 보다 작은지 아닌지를 기준으로 삼는다.

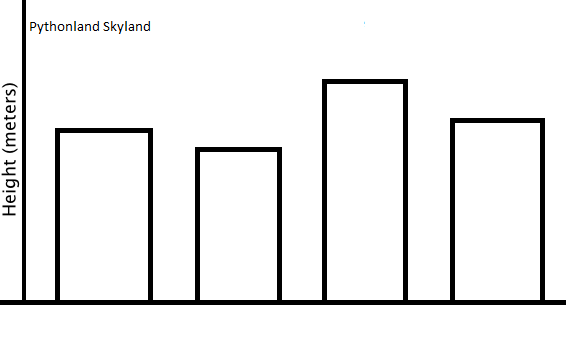
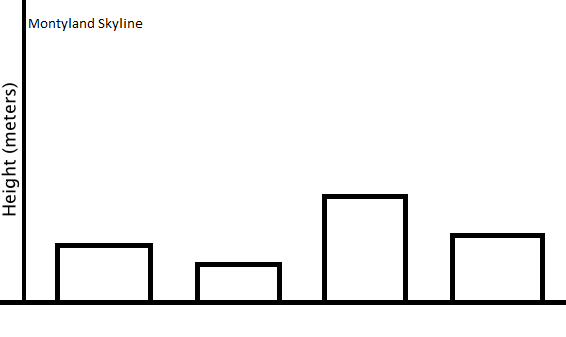
(http://courses.edx.org/courses/MITx/600.2_2x)

위 두 도시의 스카이라인중 어떤 도시의 coefficient of variance 가 더 클까?

한가지 더 생각해볼 문제가 있다. 다음의 두 변수는 CoV 를 계산하는 것이 의미가 있을까?

(1) Daily Temperature in Celsius for the city of Boston
(2) The X coordinate of a drunk in the random walk

의미가 없다. CoV 가 의미있으려면, true zero 가 있어야 한다. 바꿔 말하면 ratio scale 에 대해서만 CoV 가 의미가 있다. 위 두 수치들은 양수 또는 음수값이 있기 때문에 ratio scale 이 아니다.

Histogram

pylab 에서는 히스토그램을 어떻게 그릴까?

import pylab
import random


def exampleHist(n):
    xs = []
    for x in range(n):
        xs.append(random.random())

    pylab.hist(xs, bins=11)
    pylab.show()

exampleHist(10000)

References

(1) http://ko.wikipedia.org
(2) MIT 6.00.2 2x in edx