Cloud Computing CC 02: Gossip Protocol

CC 02: Gossip Protocol

Multicast

이번시간에 배울 내용은 Gossip Protocol (혹은 Epidemic Protocol) 입니다.

기존에는 특정 그룹에게 메세지를 보내기 위해 multicast 를 이용했지만, 클라우드 컴퓨티 환경에서는

프로세스가 죽어 노드가 크래쉬를 일으킬수도
네트워크 문제때문에 패킷이 딜레이되거나, 드랍될 수 있고
노드가 빠르게 증가합니다.

그러나 멀티캐스트는 fault-tolerance 와 scalability 측면에서 부족한 부분이 많았습니다. 이런 문제를 해결하기 위해 다양한 방법이 도입되었는데

(1) Centralized: 중앙 서버에서 TCP, UDP 패킷을 날립니다. 간단한 구현이지만 중앙서버의 오버헤드가 높고, 수천개의 노드가 있을때 latency 가 생깁니다. 노드의 수를 N 이라 했을때, 모든 노드에 메시지가 전달되는데 O(N) 시간이 걸리지요.

(2) Tree-Based: 전달 받은 노드에서, 다시 패킷을 전달하여 경로가 tree 형태로 구성됩니다. balanced tree 라면 어떤 그룹에 패킷이 전달되는데 O(logN) 의 시간이 걸립니다.

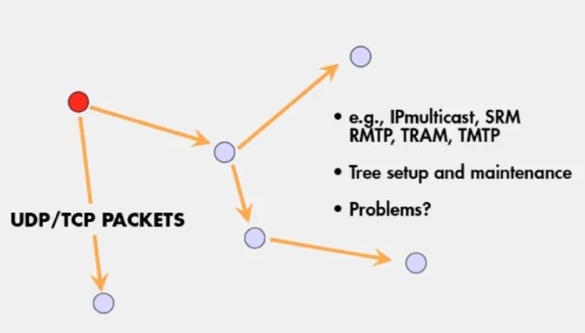
이 방법의 단점은

tree 를 구성하고 유지하는데 필요한 오버헤드
root 에 가까운 곳에서 failure 가 발생했을때의 파급력

일반적으로 tree-based multicast 프로토콜에서는 spanning tree 를 구성해서 최단비용으로 패킷을 전달합니다. 그리고 메시지가 올바르게 전달되었는지 ACK 또는 NAK 를 이용하는데 SRM 이던 RMTP 던 여전히 O(N) 만큼의 ACK/NAK 오버헤드가 발생합니다.

Gossip

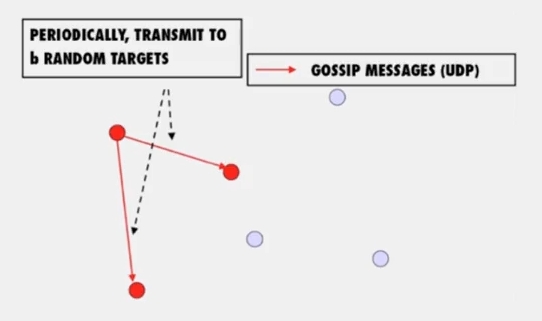
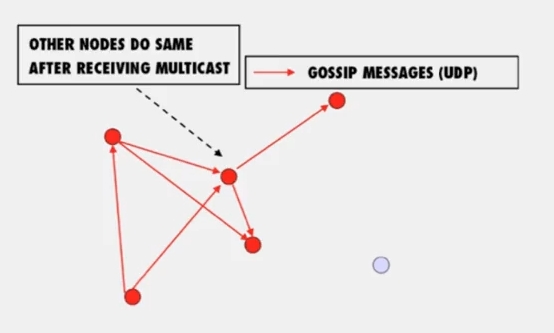
가십 프로토콜은 위 그림처럼 작동합니다.

주기적으로 랜덤한 타겟을 골라 gossip message 를 전송합니다
그리고 이것을 받아 infected 상태가 된 노드도 똑같이 행동합니다.

이걸 Push gossip 이라 부릅니다. multiple message 를 가십하기 위해 랜덤 서브셋을 선택하거나, recently-received 메시지를 를 선택하거나, higher priority one 을 고를 수 있습니다.

어떤 가십 메시지에 대해 대부분의 노드가 infected 되었을때 push gossip 은 비효율적입니다. 이때는 uninfected 노드가, 새로운 가십메시지가 있는지 주변 노드에게 물어보는 pull gossip 이 오버헤드가 더 적습니다.

Pull gossip: Periodically poll a few random selected processes for new multicast meesages that you haven’t received

Gossip Analysis

가십프로토콜은 다음의 특징을 가집니다.

lightweight in large groups
spreads a multicast quickly
highly fault-tolerant

이를 위해 간단한 증명을 해보도록 하겠습니다.

전체 n+1 의 population 에 대해
uninfected individuals 의 수를 x
infected individuals 의 수를 y
individual pair 간의 contract rate 를 β 라 하면

항상 x + y = n + 1 이고, 시작상태에서는 x_0 = n, y_0 = 1 입니다. 그리고 시간이 지날때마다 uninfected y 는 다음처럼 감소합니다.

$\frac{\mathrm{d} x}{\mathrm{d} t} = -\beta xy$

그러면 이 수식으로부터 다음을 이끌어 낼 수 있습니다.

$x = { n(n+1) \over {n + e^{\beta(n+1)t}}}$

$y = { (n+1) \over {1 + ne^{-\beta(n+1)t}}}$

그리고 infected node 가 랜덤하게 b 개의 노드를 고른다 하면 β 는

$\beta = {b \over b}$

그리고 시간 t 를 가십이 진행되는 round 라 보고 t = clog(n) 이라 치환하겠습니다. 다음을 이끌어낼 수 있습니다.

$y \approx (n+1) - {1 \over n^{cb-2}}$

이 식으로부터 gossip protocol 이 low latency, reliability, lightweight 하다는 것을 알 수 있습니다.

(1) low latency

c, b 를 n 과 독립적으로 아주 작은 숫자로 세팅하면 clog(n) round 이므로 적은 시간 내에 메시지가 전파됩니다.

(2) reliability

n 이 매우 크면 1 / n^{cb-2} 가 0 에 가까워지므로, 1 / n^{cb-2} 만큼의 노드를 제외한 모든 노드가 infected 된다는 것을 알 수 있습니다.

(3) lightweight

각 노드는 cb log(n) 만큼의 gossip message 만 전파합니다. 이론적으로는 log(N) 은 상수가 아니지만, 실제로는 아주 천천히 증가하는 숫자기에 작은 숫자처럼 생각할 수 있습니다.

Fault-Tolerance

50% packet loss 를 생각해 봅시다. b 를 2/b 로 치환하면 됩니다. 그러면 이전과 같은 reliability 0% packet loss 를 위하 두배의 round 만큼만 더 진행하면 됩니다.

node failure 는 어떨까요? 50% 노드에서 failure 가 발생한다면 n, b 을 2/n, 2/b 으로 치환하면 됩니다. 이는 contract rate 에서 가십 메시지를 전달하는 n 중 2/n 의 노드만 살아있고, 선택되는 b 중 b/2 노드만 살아있기 때문입니다. 이 경우에도 상수만 곱하면 이전과 같은 reliability 를 얻을 수 있습니다.

failure 와 관련해서 한 가지 생각해 볼 문제가 있습니다. 모든 노드가 죽는것이 가능할까요? 물론 가능합니다 초기에 모든 노드가 죽으면요. 그러나 improbable 입니다. 일단 몇개의 노드가 infected 되면, 이후에는 퍼지는 속도가 훨씬 더 빠르기 때문입니다. 루머나 바이러스가 퍼질 수 있는 이유를 생각하면 이해하기 쉽습니다.

Pull Gossip

그림에서 볼 수 있듯이, 어떤 형태의 가십 프로토콜이던 2/N 까지 전달할때는 O(logN) 만큼의 시간이 걸립니다. 그 이후에는 pull gossip 이 훨씬 빠르죠.

i round 후에 남아있는 uninfected node 의 수를 p_i 라 합시다. pull gossip 을 이용할때 다음 단계에서도 uninfected 일 확률은

$p_{i+1} = p_i^{k+1}$

이는 p_i 자체가 uninfected 여야 하고, 이 노드가 선택하는 k = b 만큼의 노드도 uninfected 여야 하는데, 이 확률은 극히 낮습니다. 슬라이드에서 보듯이 super-exponential 하고, 그렇기 때문에 second half 부터는 pull gossip 이 O(log(logN)) 입니다.

Topology-Aware Gossip

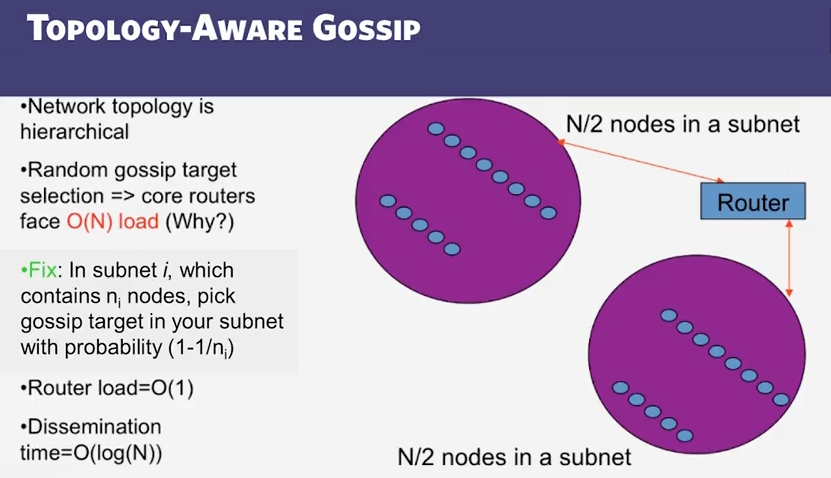
만약 uninfected node 를 uniformly random 하게 고른다면 위 그림에서 라우터의 오버헤드는 O(N) 이 됩니다. 더 정확하게는 round 마다 b * (2/n) 이 될겁니다.

이를 해결하기 위해, 서브넷에 n_i 개의 노드가 있을때 자신이 속한 서브넷에 있는 uninfected node 를 더 자주 고르게, 확률을 1 - (1/n_i) 가 되도록 합니다. 그러면, 현재 서브넷에 있는 노드를 선택할 확률이 1 에 가까우므로 O(logN) 시간 내에 전파되고, 라우터의 오버헤드는 (n_i) / (n_i) 가 되어, O(1) 이 됩니다.

Refs

(1) Title Image
(2) Cloud Computing Concept 1 by Indranil Gupta, Coursera