Algorithm Design and Analysis: Graph Search and Connectivity

Design and Analysis: Graph Search and Connectivity

기본적인 그래프 탐색 방법 DFS, BFS 에 대해 배우고 약간씩 응용하여 shortest path, conncected components, topological order, strongly connected components 등을 찾는 방법을 배운다.

마지막 부분에선 웹이 어떻게 생겼을까 잠깐 고민해 본다.

Graph Search

그래프 탐색은 다양하게 활용할 수 있다.

(1) check if a network is connected
(2) driving directoin (shortest path)
(3) formulate a plan (e.g how to fill in a sudoku puzzle)
(4) compute the “pieces” of a graph (e.g clustering)

그래프를 탐색하는데는 “재 방문하지 않는다” 등 여러 조건이 붙으면서 다양한 방법이 있을 수 있겠지만 여기서는 단순히 모든 vertex 를 방문하는 일반적인 그래프 탐색 알고리즘 (generic algorithm) 에 대해 먼저 이야기 해 보자.

이렇게 먼저 일반적인 알고리즘을 정의해 보는 이유는, BFS 와 DFS 를 증명할때 먼저 정의한 일반적인 알고리즘의 특수한 경우임을 파악하여 이미 증명된 결과를 활용할 수 있기 때문이다.

Goals: find everything findable from a given start vertex, O(m + n)

여기서 findable 이란 말은 두 점 (s, e) 사이에 path (경로) 가 있냐는 질문과 동일하다. 경로가 없으면 findable 이 아니다.

목표로 하는 복잡도가 O(m + n) 인데, 이것은 정점의 수 n 이나 엣지수 m 중 더 큰 수를 따라간다고 이해하면 된다. 알고리즘은 이렇다.

initially `s` explored, all other vertices are unexplored  
while possible:  
  choose an edge `(u, v)` with `u` explored and `v` unexplored  
  mark `v` explored

generic graph search algorithm 이 끝났을때 v 가 explored 라면 그래프 G 가 s -> v 인 path 가 존재한다. 이를 귀납법으로 증명해 보자.

귀납법이므로 먼저 증명하려는 바를 부정하여 알고리즘이 종료 되었을 때 G 에서 (s -> v) 로 가는 경로가 없다고 하자.

알고리즘 초기 단계에서 s 만 explored 고 나머지는 unexplored 다. 매 탐색마다 (u, w) 를 찾아내며 unexplored w 를 explored 로 마킹한다.

(s, v) 사이 경로가 없다면, 어떤 w 가 unexplored 인 (u, w) 가 알고리즘이 끝났을때 존재해야 한다. w 가 v 일수도, u 가 s 일수도 있다.

그러나 이 경우 unexplored w 가 존재하면 알고리즘이 절대 종료될 수 없다. 결국 모순이므로 s -> v path 가 없다는 것이 잘못되었다.

BFS vs DFS

사실 그래프 탐색 문제는 crossing edge 문제와 같다. 한쪽을 explored, 다른쪽을 unexplored 라 놓고 각 vertex 들을 잇는 crossing edge 를 고르는 문제다.

BFS 는 기본적으로 queue 를 사용하면 O(m + n) 이다. 그리고

(1) explore nodes in “layers”
(2) can compute “shortest path”
(3) can compute connected components of an undirected graph

DFS 는 stack 을 이용하면 O(m + n) 이다. 그리고

(1) explore aggressively like a maze, backtrack only when necessary
(2) compute topological ordering of directed acyclic graph
(3) compute connected components in directed graphs

Breadth-First Search

BFS 는 shortest path 를 계산할 수 있고 undirected graph 의 connected components 를 구할 수 있다. 그리고 복잡도는 O(m + n) 이다.

함수를 BFS(graph G, start-vertex s) 라 하면 시작단계에서는 모든 그래프 노드가 unexplored 다.

(1) mark s as explored
(2) Let Q - queue data structure (FIFO), initialied with s
(3) while Q is not empty:
- remove the first node of Q, call it v
- for each edge (v, w), if w unexplored mark w as explored and add w to Q

시작 점 s 를 layer 0 이라 부르면 layer 1 은 layer 0 에서 갈 수 있는 지점이다. 모두 저장하고, 큐에서 하나 꺼내 layer 2 를 계산해서 다시 집어넣고, 이 과정을 반복한다. 알고리즘 중에 이미 방문했는지를 검사하기 때문에 같은 노드를 두번 이상 방문하지 않는다.

알고리즘이 종료되었을때 v 가 explored 라면 s -> v 인 path 가 존재한다. 증명은 간단한데 BFS 가 generic search algorithm 의 spcial case 이기 때문이다.

BFS 알고리즘을 잘 보면 generic algorithm 처럼 (u, w), w 는 unexplored 인 edge 를 찾는데, 이 때 BFS 는 한 레이어에서 다음 레이어로 갈 수 있는 edge 만 찾는다는 점이 다르다.

running time 은 O(n_s + m_s) 다. 여기서 n_s 는 s 에서 갈 수 있는 node 의 숫자고 m_s 는 s 에서 갈 수 있는 edge 수다.

while 루프 알고리즘을 다시 보면

while `Q` is not empty:  
  remove the first node of `Q`, call it `v`  
  for each edge `(v, w)`:
    if `w` is unexplored:
      mark `w` as explored
      add `w` to Q

한 vertex 는 아무리 많아봐야 큐에 한번 들어가고, 이 때마다 이 vertex 에서 갈 수 있는 edge 를 검사하지만, 결국 아무리 많아봐야 한 edge 당 두번씩만 검사되고, 검사하는 for 구문은 O(1) 이기 때문에 O(m + n) 이다.

Shortest Path

생각해보면 굉장히 쉽다. s 부터 시작해서 v 까지의 거리를 찾는 경우 s = v 면 각 노드의 dist 값을 0 으로, 아니면 무한히 큰 값으로 한다.

BFS 에서 레이어마다 하나씩 넘어갈때 마다 dist 값을 1씩 증가시키는데, 이때 이미 dist 값이 있는 경우 그 값보다 적으면 새로운 dist 값을 기록하고, 아니면 기록하지 않는다.

따라서 알고리즘이 종료되었을때 dist(v) = i 라면 v 는 i 번째 레이어에 있다. 바꿔말하면 shortest path (s, v) 는 i 개의 edge 를 가지고 있다는 뜻이다.

Undirected Connectivity

undirected connectivity 는 그래프에서 서로 연결된 부분 집합을 찾는 문제다. 용어부터 정의하고 가자면

equivalence classes of the relation u ~ v <=> E(u, v) path in G

equivalence class 는 처음봤는데 위키에 보니 다음의 3 가지 속성을 만족한다고 한다.

For every element a in X, a ~ a (reflexivity)
For every two elements a and b in X, if a ~ b, then b ~ a (symmetry)
For every three elements a, b, and c in X, if a ~ b and b ~ c, then a ~ c (transitivity)

connected component 를 어디다 쓸 수 있을까?

네트워크에 대해 적용해 보면, 네트워크가 끊어졌는지를 connected component 를 구해서 두개 이상이 나오는지로 판단할 수 있다.

clustering 에도 쓸 수 있다. 만약 두 유전자나, 웹페이지가 비슷한지를 비교해서 connected component 로 만들면 구별되는 특징을 가진 집단을 만들 수 있다.

clustering 하는 다른 알고리즘이 많음에도 BFS 는 linear time 이기 때문에 clustering 에 충분히 쓸만하다.

undirected 그래프에서 BFS 를 이용하면 conncected component 를 구하는 알고리즘은 이렇다.

all node unexplored // assume labelled 1 to n

for i = 1 to n
  if i not yet explored
    BFS(G, i)

따라서 BFS 를 수행할 때 마다 connected component 가 하나씩 나온다고 말할 수 있다.

성능은 마찬가지로 O(m + n) 이다. 왜냐하면 부의 if 나 for 그리고 모든 노드를 unexplored 로 초기화 하는 부분도 O(n) 이고, 각 노드 하나씩에 대해서 방문하지 않았을 때만 BFS 를 수행하는데 BFS 는 edge 에 대해서는 O(1) 이고, 모든 edge 를 검사하므로 BFS 의 전체 성능은 O(m) 이다. 따라서 O(m + n)

Depth-First Search

explore aggressively, and backtrack when necessary

BFS 로도 O(m +n) 시간 내에 탐색하고 shortest path, connected component 를 찾는데 왜 DFS 가 필요할까?

(1) can computes a topological ordering of a directed acyclic graph
(2) strongly conncected components of directed graphs

BFS 는 못하는 이 두 가지 문제를 O(m + n) 으로 해결할 수 있다.

코드는 비슷한데 queue 대신 stack 을 쓰도록 하고, 재귀버전으로 작성해 보자.

DFS(graph G, start-vertex s)

mark s as explored

for every edge (s, v):
  if v is unexplored
    DFS(G, v)

DFS 가 종료 됐을때 v 가 explored 라면 s -> v 인 path 가 있다. 이는 DFS 가 위에서 본 generic search algorithm 의 특별한 케이스임을 생각하면 쉽게 알 수 있다.

성능은 BFS 와 같이 O(n_s m_s) 인데, 각 vertex 는 아무리 많아봐야 한번, edge 는 아무리 많아봐야 두번씩 체크하고 edge 내부에서의 연산은 O(1) 이기 때문이다.

Topological Sort

정의부터 보면

A toplogical ordering of a directed graph G is a labelling f of G’s nodes such that
1. the f(v)’s are the set {1, 2, 3, ..., n}
2. (u, v) in G => f(u) < f(v)

이미지로 보면 더 이해하기 쉽다.

(http://www.stoimen.com)

왜 topological sort 가 필요할까? precedence constraints 가 있는 sequence 에서 나올 수 있는 모든 경우의 수를 파악하기에 좋다. 예를 들어 선수과목이 있을때 이수 가능한 스케쥴이라던가, 일정이라던가.

Sequence taks while respecting all precedence constraints

단, topological sort 를 하기 위한 조건이 하나 있는데 directed cycle 이 없어야 한다. 다시 말해 acyclic 이어야 한다.

If G has directed cycle, then no topological ordering

directed graph 에서 outgoing edge 가 없는 것을 sink vertex 라 하자. 그러면 directed acyclic graph, DAG 는 최소한 하나의 sink vertex 를 가지고 있다.

증명은 contradiction 을 이용하자. sink vertex 가 없다고 하면, 쭈욱 방문하다 보면 하나의 vertex 를 두번 이상 방문하게 되고, 그건 cyclic 이므로 acyclic 이란 조건에 위배되므로 모순이다. 따라서 DAG 에서는 최소한 하나의 sink vertex 가 있다.

topological sort 의 알고리즘은

let v be a sink vertex of G
set f(v) = n
recurse on G - {v}

G - {v} 도 DAG 이다. 왜냐하면 DAG 에서 sink vertex 를 제거해도 DAG 이기 때문에 매 재귀마다 G 는 DAG 가 된다. 이 때 제거하는 sink vertex 에 전체 노드 수 n 을 매기기 때문에 최종적으로는 1, .., n 을 가진 toplogical order 을 계산할 수 있다.

이제 DFS 를 이용해 toplogical sort (위상 정렬) 을 해보자.

DFS(graph G, start-vertex s)
- mark s explored  
- for every edge (s, v):
    if v not yet explored:
      DFS(G, v)
- set f(s) = current_label // sink vertex
- current_label--
    
DFS-Loop(graph G)
- mark all nodes unexplored
- current_label = n // to keep track of ordering
- for each vertex v in G:
    if v not yet explored:
      DFS(G, v)

running time 은 O(m + n) 이다. node 마다 O(1), edge 마다 O(1) 이고 node 나 edge 는 두번 방문하지 않기 때문에 (directed graph) O(m + n)

위상정렬을 하는지는 (u, v) 가 edge 라면 f(u) < f(v) 임을 보이면 된다.

u 먼저 방문되었을 경우에는 v 가 먼저 끝나 n 이 할당되기 때문에 f(u) < f(v) 다.

만약에 v 가 u 보다 먼저 방문되면 u 가 방문되기도 전에 v 에 대한 방문이 끝나므로 f(u) < f(v) 다.

Strongly Connected Components

먼저 정의부터 보면

Strongly conncected components (SCCs) of a directed graph G are the equivalence classes of the relation. u ~ v means path u -> v and v -> u in G

directed graph 는 방향성이 있기 때문에 단순히 component 를 구한다고 해서 equivalence classes 가 되지 않는다. 서로 순환이 될 수 있는, cyclic 인 component 를 찾아야 한다.

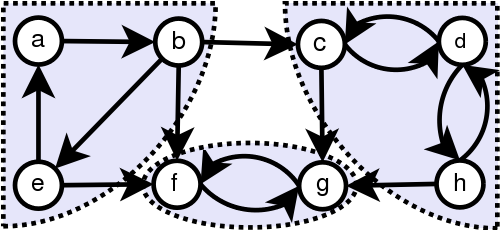
(http://commons.wikimedia.org)

SCC 는 cycle 이기 때문에 DFS 만 돌려도 나올 수 있다. 그런데, 만약 전체로 갈 수 있는 노드에서 DFS 를 돌려버리면 모든 SCC 가 합쳐진 형태가 나온다. 다시 말해서 단순 DFS 를 모든 노드에 대해 돌리는 것으로는 SCC 를 얻을 수도, 못 얻을 수도 있다는 소리다. Kosaraju’s Two-Pass Algorithm 으로 해결할 수 있다.

Kosaraju’s 2-pass algorithm

O(m + n) 으로 SCC 를 구하는 것을 보장한다. 어떻게 그럴까? SCC 를 찾을 때 DFS 를 돌릴려면 특정 노드의 순서로 DFS 를 돌려야 한다. 그렇지 않으면 SCC 가 나오지 않는다. Kosaraju algorithm 은 이 순서를 찾아준다.

Let G_rev = G with all arcs reversed
run DFS-Loop on G_rev // compute "magical ordering"
run DFS-Loop on G // discover SCCs

좀 더 자세히 보면 f(v) 를 각 vertex 에 대해 finishing time 이라 보면, 두번째 DFS-Loop 에서 f(v) 의 decreasing order 로 DFS 를 여러번 돌리면 SCC 를 찾아준다. 각 함수의 구현을 보면

DFS-Loop(graph G)

global variable t = 0 // # of nodes processed so far
global variable s = NULL // current source vertex

// assume nodes labelled 1 to n
for i = n to 1 by -1:
  if i not yet explored:
    s := i
    DFS(G, i)

DFS(graph G, node i)

mark i as explored
set leader(i) := node s

for each arc (i, j) in G:
  if j not yet explored:
    DFS(G, j)

t++
set f(i) := t

첫번째 DFS-Loop 에서는 edge 가 뒤집어져 있다. 함수가 끝나면 각 노드마다 f(t) 를 계산 해 주는데, 이게 사실 SCC 기준으로 보면 같은 SCC 내에서는 외부와의 연결고리가 없는 내부 노드가 가장 낮은 f(t) 를 가지게 된다.

이제 두번째 DFS-Loop 를 돌리기 위해 edge 를 다시 뒤집어서 보면 가장 높은 f(t) 값을 가지는 노드가 가장 먼저 DFS 를 돌려야 할 노드가 된다. 그리고 leader 는 각 SCC 를 얻기 위해 DFS 를 시작해야 할 지점이 된다.

running time 은 2 x DFS 기 때문에 O(m + n) 이다. 첫 번째 노드에서 얻은 finisihing time f(t) 를 정렬하면 O(n logn) 이기 때문에 정렬 없이 decreasing 순서로 DFS 를 돌게 해줘야 한다.

Analysis

분석에 앞서서 간단한 성질을 먼저 이끌어 내자. 그래프를 변형해 node 각각을 SCC 로 만든 meta-graph 를 생각 해 보자. 이 meta graph 는 DAG 다. 왜냐하면 모든 cycle 있는 그래프는 SCC 로 포함되었기 때문이다.

따라서 G 나, 여기서 edge, arc 를 뒤집은 G_rev 나 같은 SCC 를 가지고 있다.

이 때 G 에서 서로 인접한 SCC C1 -> C2 에 대해서 edge (i, j) 가 있다고 해 보자. (i -> j)

그러면 G_rev 로 계산한 max f(C1) < max f(C2) 임을 알 수 있다. 다시 말해 C2 가 먼저 DFS 를 돌려야 하는 SCC 인데, 먼저 돌려야 할 수록 더 높은 finishing time f(t) 를 가진다.

이건 쉽게 보일 수 있는데, G_rev 에서는 arc 가 반대 방향이 되므로 더 큰 SCC C1 이, 다시 말해 더 나중에 계산해야 할 SCC 가 더 작은 SCC 가 되므로 먼저 계산이 끝나 더 작은 max f(t) 를 가지게 된다.

증명은 C1 union C2 의 첫번째 노드가 C1 에 있을 때 C2 에 있을때로 각각 나눠서 참임을 보이면 쉽다.

알고리즘을 다시 보면

DFS-Loop(graph G)

global variable t = 0 // # of nodes processed so far
global variable s = NULL // current source vertex

// assume nodes labelled 1 to n
for i = n to 1 by -1:
  if i not yet explored:
    s := i
    DFS(G, i)

DFS(graph G, node i)

mark i as explored
set leader(i) := node s

for each arc (i, j) in G:
  if j not yet explored:
    DFS(G, j)

t++
set f(i) := t

DFS 를 한번 돌릴 때 마다 SCC 가 하나씩 발견된다. 우선 sink SCC 가 가장 높은 f(t) 값을 가지게 되므로 가장 먼저 DFS 를 돌게 된다. 그리고 SCC 는 cyclic 이므로 하나의 SCC 만 찾고 끝남을 보장한다. 다음으로 높은 f(t) 값을 가지는 SCC 를 찾고, 더이상 SCC 를 찾지 못할 때 까지 반복하고 알고리즘이 끝나는걸 확인할 수 있다.

처음엔 잘 몰랐는데 leader 가 해당 SCC 에서 가장 높은 f(t) 값을 가지는 node 다.

Structure of the Web

vertices 를 웹페이지라 보고 edges 를 하이퍼링크라 보면 웹을 directed graph 이해할 수 있다.

그럼 웹은 어떻게 생겼을까? 사람들이 첫번째로 웹이 어떻게 생겼는지 확인하기 위해 시도한 방법은 crawling, 즉 링크를 따라가며 모든 웹페이지를 긁는 방식이었다.

그래서 실제로 해보니 2000 년도에는 200 milions 의 node, 1 bilion 의 edge 가 있었다고 한다.

그럼 이게 어떻게 생겼을까? one big scc 일거라 보는 관점이 있다. 한쪽에선 오래된 웹페이지들이 있고, 더 뻗어나가지 않는다. 이쪽을 out 이라 보면 반대편에서는 새로운 웹페이지들이 생겨 기존의 웹페이지에 edge 를 붙여 나가는 in 부분이 있다고 할 수 있다. 몇몇 부분에는 전혀 연결이 되지 않은 부분이 있을 수 있다.

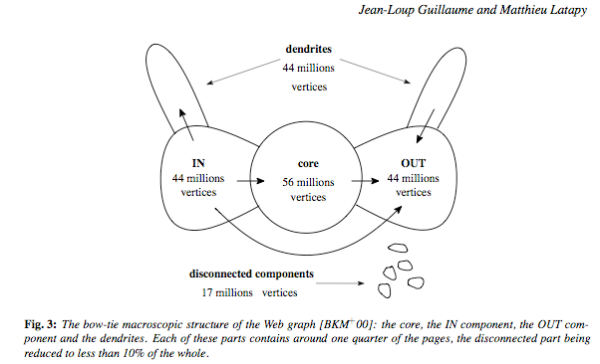
(http://bparsia.wordpress.com)

웹의 core 부분은 well connected 되어 있는데 small world property 를 가지고 있다. 무슨말이냐면 모든 노드가 각각 서로 연결되어 있진 않지만 연결을 많이 가지고 있는 특정 몇몇 노드에 의해 모든 노드가 연결된다는 뜻이다. 결국 서로 연결되는데 몇 hop 안걸린다 볼 수 있다.

(http://en.wikipedia.org/wiki/Small-world_network)

(http://web.mit.edu )

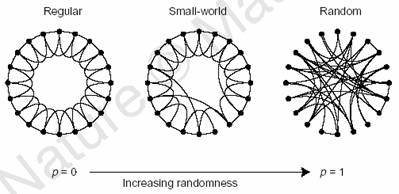
요즘의 연구들은 웹 그래프가 어떤식으로 진화하는지, 정보들이 어떤식으로 전파되는지 등을 중점으로 하고 있다.

References

(1) Algorithms: Design and Analysis, Part 1 by Tim Roughgarden
(2) Equivalence class
(3) http://www.stoimen.com
(4) http://commons.wikimedia.org/wiki/File:Scc.png
(5) http://bparsia.wordpress.com
(6) http://web.mit.edu
(7) http://en.wikipedia.org/wiki/Small-world_network