AI Planning 3: PSP, PoP

Partial Plan

이 전까지는 plan 을 goal state 를 달성하기 위한 action 의 나열로서 봤다. plan 자체를 하나의 솔루션으로 본 것이다. partial plan 은 이와 달리, 탐색 공간이 state 가 아니라 plan 으로 구성되어있다는 생각에서 시작한다.

• state-space search: search through graph of nodes rpresenting world states
• plan-space search: search through graph of plans.

(1) nodes are partially specified plans.
(2) arcs are plan refinement opreations.
(3) solutions are partial-order plans.

partial plan 이란

• subset of the actions
• subset of the organizational structure including temporal ordering of actions and rationale (what the action achieves in the plan)
• subset of varaible bindings

좀 더 formal 한 정의는

• A 는 partially instantiated 된 operators 다.
• < 는 ordering constraint
• B 는 variable binding
• L 은 casual links 로 action 간 ordering 과 여기에 필요한 proposition (effect, precond), binding constraint 를 포 함한다. a_i 를 producer a_j 를 consumer 라 부르기도 한다.

Plan Refinemeents

partial plan 의 구성요소는

• initial state
• goal conditions
• set of operators with different varaibles

Adding Actions

unsatisfied pre-cond, unsatisfied goal condition 을 위해서 partial plan 에 action 을 추가해야 한다. forward search 나 backward search 에서는 앞이나 뒤에만 action 을 추가할 수 있었지만 partial plan 에선 그런 제약이 없다.

예제를 보면 initial state 와 goal 로만 구성된 empty plan 에서 시작해서 partial plan 을 점점 키워간다.

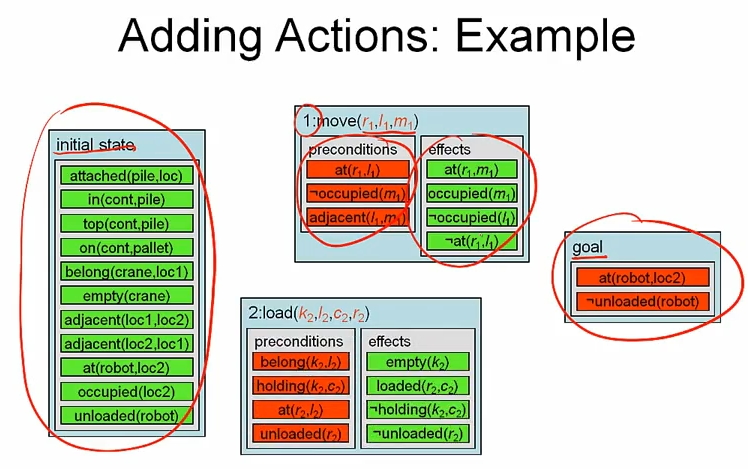
Adding Casual Links

위에서 언급했듯이 partial plan 은 action 간 casual links 를 포함하고 있다. action 간 invalid pre-cond, effect 를 방지하기 위해서 필요하다.

두 종류의 provider 가 있을 수 있다.

(1) action 의 effect
(2) initial state 를 담고있는 atom

마찬가지로 consumer 도

(1) action 의 pre-condition 거나 (2) goal condition 일 수 있다.

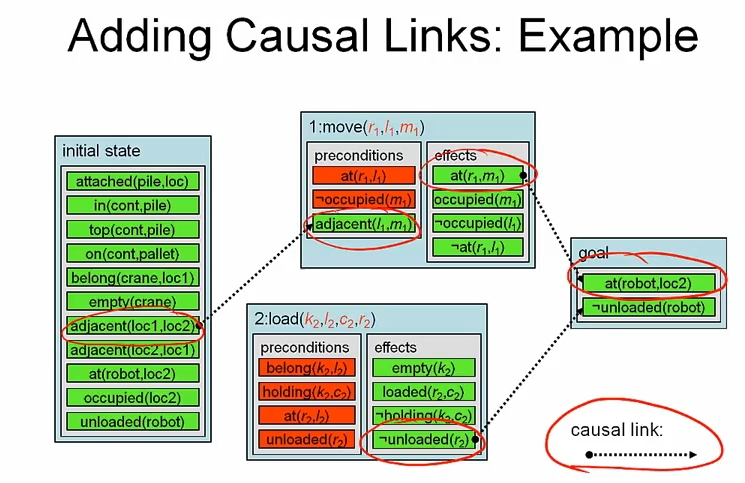
Adding Variable Bindng

• new operators introduce new (copies of) variables into the plan
• solution plan must contain actions
• varaible binding constraints keep track of possible values for varaibles and co-designation

새로운 operator 가 사용될때 마다, 새로운 varaible 이 plan 에 추가된다. 그런데 솔루션에는 action 이 있어야 하므로 possible value 를 테이블로 유지해야 한다. casual links 를 추가하면서 effect 와 pre-cond 를 연결했지만, variable 까지 고려하면 invalid 한 경우가 생길수도 있으므로 이를 막기 위해 varaible binding 이 필요하다. 예제를 보면

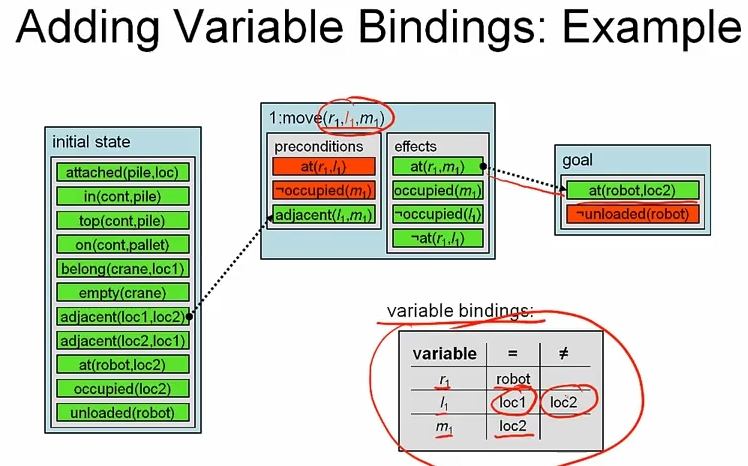
Adding Ordering Constraints

partial plan 은 ordering constraint 를 포함하고 있다.

• binary relation specifying the temporal order between actions in the plan

ordering constraints 를 추가해야 하는 이유는

• all actions must come after initial state
• all actions must come before goal
• casual link implies ordering constaint
• to avoid possible interference between actions

예제를 보자. 그림에서 variable binding 이 표시되어 있진 않지만, 있다고 보자.

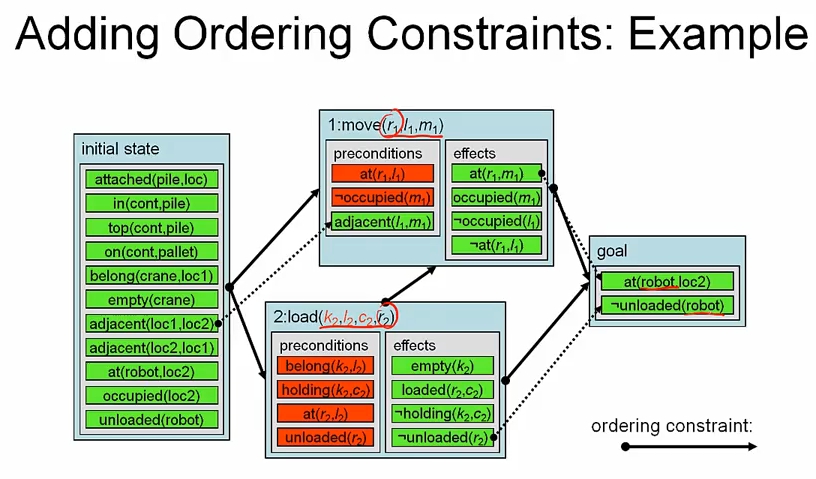
Plan-Space Search

지금까지 partial plan 을 구성하는 방법에 대해 배웠고, 이제 partial plan 을 노드로 삼는 plan-space search 에 대해 알아보자.

최초에는 두개의 더미 action 인 init, goal 을 가지고 init < goal 의 ordering constaint 를 가진다.

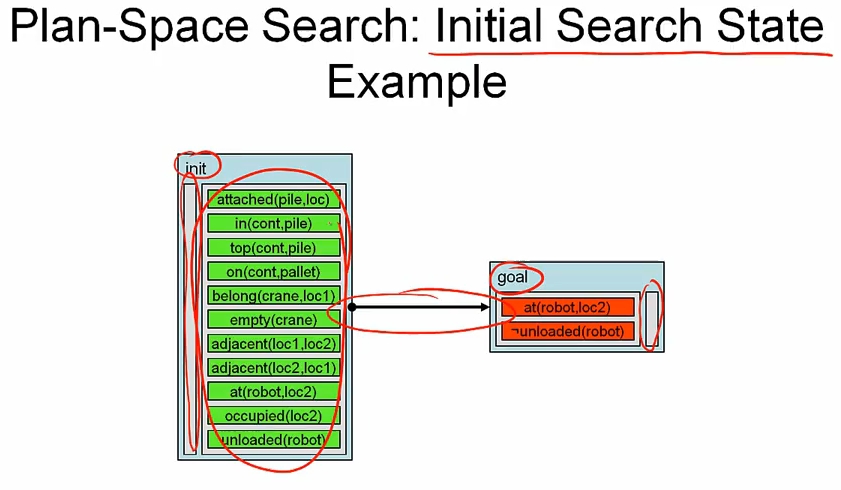
이제 plan refinement operators 를 적용해서 하나 이상의 successor 를 찾기 위한 successor function 을 정의해 보자.

• adding an action to A
• adding an ordering constaint to <
• adding a binding constaint to B
• adding a casual link to L

보면 알겠지만 plan-space search 는 두 가지 문제를 decoupling 한다.

(1) which actions to execute as part of our plan
(2) how to organize these actions?, what is the organizational structure that underlies our plan?

plan-space search 를 다른관점에서 볼 수도 있다. possible plan 을 partial plan 으로 줄여가는 것이다.

planning problem P 는 state transition system, initial state, goal 로 구성된다. 이때 plan ㅠ 에 대해 r(s_i, ㅠ) 가 g 를 만족시키면, ㅠ 는 솔루션이다.

r(s_i, ㅠ) 는 ground action 의 시퀀스로만 정의되는데

• partial order corresponds to total order in which all partial order constaints are respected
• partial instantiation corresponds to grounding in which variables are assigned values consistent with binding constraints

생각해보면 partially instantiated varaibles 을 fully ground plan 으로 바꿀 수 있는 경우의 수가 많기 때문에 어떤 것을 사용할지 결정해야 한다. 이를 위해 partial order solution 을 정의하면

위 슬라이드에서 볼 수 있듯이 두 가지 조건이 갖추어지면 plan ㅠ 가 (partial order) solution 이 될 수 있다.

• its ordering constaints < and binding constraints B are consistent and
• for every total order seq <a1, ... , ak> of all the actions in A - {init, goal} that is

(1) totally ordered and grounded and respects < and B
(2) r(s_i, <a1, ..., ak>) must satisfy g

흥미로운점은 casual links 가 아무런 역할도 하지 않는다는 것이다. 두번째는 위 과정을 goal test 로 쓰기 위해 computational procedure 로 바꾸면, 퍼포먼스가 별로라는 사실도 알 수 있다.

만약 우리가 모든 total order seq 를 테스트 해야하고, 수 많은 seq 가 있다면 goal 을 검증하기 위해 수 많은 작업을 해야한다.

물론 plan 을 만드는 과정에서 action 의 pre-cond 가 casual links 에 의해 지정되기 때문에, 우리가 만들고 있는 plan 이 goal 을 만족하는지, 아닌지 알 수 있다. 문제는 pre-cond 만으로는 goal 을 만족하는지 아닌지 충분하지 않다는 점이다.

Threats and Flaws

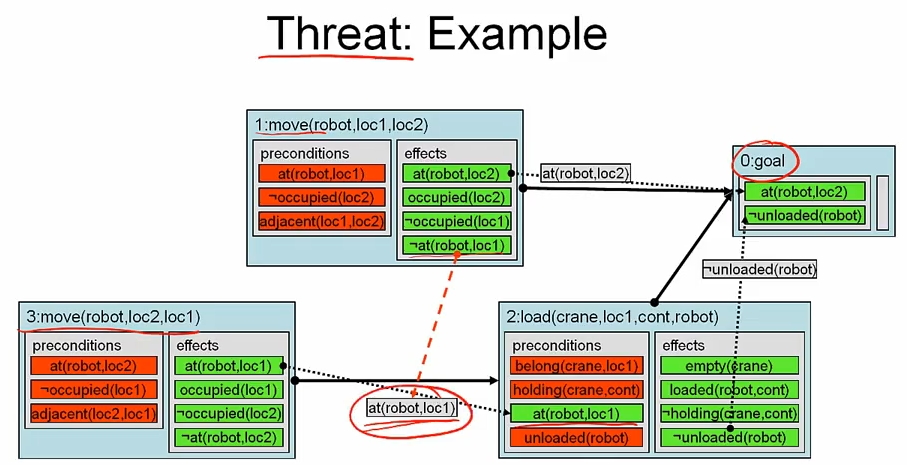
위 그림에서 action 3 과 1 은 at(robot, loc1) 을 서로 추가하고, 삭제한다. 따라서 병렬로 실행되면 dummy action 인 goal 이 실행되지 않을 수 있다. 이 경우를 threat 라고 부르며, 간단한 해결 방법으로 action 2 에서 1 로 ordering 을 추가할 수 있다. 정의를 보면

casual link a_i -> [p] -> a_j 에 에 대해 threat a_k 는 p 와 unifiable effect ~ q 를 가지고 있고, ordering constraint a_i < a_k, a_k < a_j 가 있다. 다시 말해 a_i 의 effect 를 상쇄할 수 있다는 말이다.

unsatisfied sub-goal 과 threat 같은 것들을 flaw 라 부른다.

만약 partial plan ㅠ = (A, <, B, L) 가

(1) ㅠ has no flaws
(2) the ordering constaints < are not circular
(3) the variable bindings B are consistent

이면 partial plan ㅠ 는 planning problem P 의 솔루션이다.

PSP algorithm

plan-space planning 을 잠깐 복습해보면,

operator, initial state goal 로 구성된 planning problem 이 주어졌을때, search problem 은 위 슬라이드처럼 정의할 수 있다.

PSP, Plan-Space Planner 의 기본적인 아이디어는 partial plan ㅠ 가 flaw 가 없을때 까지 <, B 를 valid 하게 유지하면서 refine 하는 것이다. 따라서 flaw 를 찾고, 이걸 해결할 수 있는 resolvers 를 구한 뒤 적절히 선택해 나아가면 된다. 알고리즘은

function PSP(plan)
  allFlaws <- plan.openGoals() + plan.threats()
  
  if allFlaws.empty() then return plan
  
  flaw <- allFlaws.selectOne()
  allResolvers <- flaw.getResolvers(plan)
  
  if allResolver.empty() then return failure
  
  resolver <- allResolvers.chooseOne()
  newPlan <- plan.refine(resolver)
  
  return PSP(newPlan)

여기서 chooseOne() 과 selectOne() 이라는 두개의 선택 함수를 볼 수 있는데

• chooseOne() is non-deterministic choice
• selectOne() is deterministic selection

chooseOne() 의 경우 non-deterministic 이기 때문에 실패할 경우 backtracking 할 수 있도록 해야 한다.

반면 selectOne() 은 deterministic 이기 때문에 backtracking 이 필요 없다. 대신 고려해야 할 것은

(1) order 가 effcientcy 에 영향을 미치기 때문에 어떤걸 선택하느냐가 중요하다. (order 는 completeness 와는 관련 없다)
(2) 모든 flaw 는 plan 이 solution 이 되기 전에 resolved 되야 한다.

PSP Implementation

function PSP(plan)
  allFlaws <- plan.openGoals() + plan.threats()
  
  if allFlaws.empty() then return plan
  
  flaw <- allFlaws.selectOne()
  allResolvers <- flaw.getResolvers(plan)
  
  if allResolver.empty() then return failure
  
  resolver <- allResolvers.chooseOne()
  newPlan <- plan.refine(resolver)
  
  return PSP(newPlan)

unachieved sub-goal 의 리스트는 action 을 추가하면서 precondition 때문에 늘어나고, casual link 을 추가할때는 protected proposition 때문에 감소한다.

threat 의 경우에는 새로운 액션 a_new 에 대해 기존의 링크 L 내에 있는 모든 a_i -> [p] -> a_j 에 대해 a_new < a_i, a_j < a_new 인지 검사하고, 참이면 패스한다. 참이 아닐경우 p 와 ~q 의 effect 가 상쇄되는지 검사하여 threat 인지 검사한다.

casual link a_i -> [p] -> a_j 를 추가할때는 기존의 action a_old 에 대해 threat 가 될 수 있는지 위처럼 검사한다.

먼저 unachieved precondition 을 제거하는 resolver 를 구하는 방법을 알아보자. 기존의 valid action 의 effect q 에 대해 unachieved precondition p 를 해겨할 수 있으면 resolver 를 추가한다. operator 로 부터 직접 action 을 만들어 casual link 까지 추가할 수도 있다.

threat 를 제거하는 resolver 는 위처럼 구할 수 있다. a_i -> [p] -> a_j 에 대한 threat a_t 에 대해 a_t < a_i, a_j < a_t 를 추가하거나, variable binding 을 추가하는 방법이 있다. v 의 substitution 이 v 와 다르면서, 동시에 B 와 consistent 해야만 resolver 다.

ordering 이나 binding constraints, casual links, new action 을 추가하면서 refinement 를 할 수 있다. 이 때 resolver 를 찾기 위한 unachieved precondition, threat 를 업데이트 해야 한다.

ordering constaints 는 질의하거나, 새로운 ordering 을 추가하기 위해 유지해야 한다. 이를 위한 표현 방법으로 위 슬라이드처럼 3가지 방법중 하나를 사용할 수 있다.

transitive closure 를 유지하는 방법의 경우, query (질의) 는 빠르나 새로운 연산의 추가가 느릴 수 있다. 그러나 planner 의 경우 query 가 더 자주사용되는 연산이므로 좋은 표현 방법이다.

unary constriants 와 equality 는 linear time 으로 구할 수 있다. inequality 의 경우에는 exponential time 이 필요하고, 일반적으로 NP-complete 문제라고 알려져 있다.

inequality 를 도입하는 것은 threat 를 풀 수 있는 resolver 이기 때문에 꼭 필요한데, 퍼포먼스가 문제가 될 수 있다.

sound 는, planner 가 리턴하는 것이 solution 이란 뜻이고 complete 하다는 것은 solution 이 있으면 planner 가 반드시 찾아낸다는 뜻이다.

The PoP Planner

Partial Order Planning

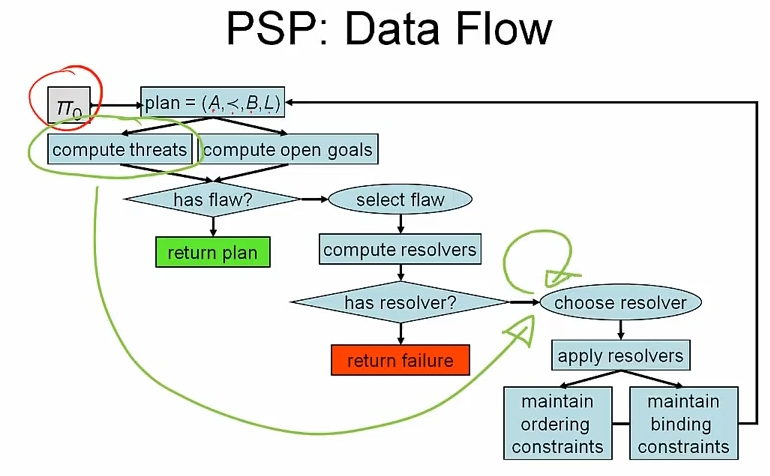
PoP 플래너는 모든 threat 를 위 슬라이드에 표시된 초록색 부분에서 루프로 다룬다.

action, precondition 을 하나의 set 으로 하여 agenda 라는 input 으로 취급한다. 그리고 flaw type 에 의해서 search control 이 진행된다. 코드로 보면

funciton PoP(plan, agenda)
  if agenda.empty then return plan
  
  (a_g, p_g) <- agenda.selectOne()
  agenda <- agenda - (a_g, p_g)
  relevant <- plan.getProviders(p_g)
  
  if relevant.empty() then return failure
  
  // non-deterministic, use backtracking
  (a_p, p_p, σ) <- relevant.chooseOne() 
  plan.L <- plan.L ∪ <a_p -> [σ(p_g)] -> a_g>
  plan.B <- plan.B ∪ σ
  
  if a_p is not in plan.A then
    plan.add(a_p)
    agenda <- agenda + a_p.preconditions
    
  newPlan <- plan
  
  for each threat on <a_p -> [p] -> a_g> or due to a_p do
    allResolvers <- threat.getResolvers(newPlan)
    
    // backtracking
    if allResolvers.empty() then return failure
    
    resolver <- allResolvers.chooseOne()
    newPlan <- newPlan.refine(resolver)
    
  return PoP(newPlan, agenda)

back-propagation 과 비슷하게 goal 부터 시작한다. plan 의 casual links, binding 을 추가해 가면서 진행한다.

State-Space vs Plan-Space

state-space 플래너와 plan-space 플래너를 비교하면,

(1) state-space 는 유한한 탐색 공간을 가진다. 매 스탭마다 유한한 수의 오브젝트와 릴레이션을 다루기 때문이다. 반면 plan-space 에선 탐색공간이 무한할 수 있다. 그러나 무한한 공간을 모두 다 탐색하는 것은 아니고, 솔루션을 찾기 위해 그 일부만 탐색한다.

(2) state-space 는 보통 graph 로 표현되고, 실제로는 tree 를 탐색한다. 반면 plan-space 에서는 어떤 intermediate representation 을 사용하는지 명확하지 않다. 이건 상당히 중요한데, 대부분의 모던 휴리스틱 기법들이 explicit representation of intermediate states 에 의존하기 때문이다.

(3) state-space 기법에선 action ordering 이 어떻게 탐색할지를 결정하는 반면 plan-space 에서 action 의 선택과 organization 은 독립적이다. 더 유연하다.

(4) state-space 에선 casual structure 가 implicit 한 반면 plan-space 에선 casual links 라는 explicit representation 으로 보여진다. 왜 이 action 을 사용하는지에 대한 명확한 기준이 있기 때문에 current plan 이 잘못되었을 때 수정하기 더 쉽다.

(5) state-space 에서는 search-node 가 더 간단하다. set of ground atoms 기 때문에 successor 를 계산하기도 더 쉽다. 반면 plan-space 에서는 constraint network 를 유지해야 하기 때문에 복잡하고, successor 를 계산하기도 쉽지 않다.

요즘에는 효율적인 휴리스틱 때문에 state-space 가 좀 더 많이 이용되는 편이라고 한다.

Refs

(1) Artificial Integelligence Planning, by Dr.Gerhard Wickler, Prof. Austin Tate
(2) brain image