AI Planning 2: A*. STRIPS

이번 시간에는 A* algorithm, heuristics, forward search 등을 배운다.

Heuristic Search Strategies

FIFO 나 LIFO 는 와 달리 heuristic algorithm 은 search space 에 대한 정보를 이용한다.

heuristic function h: state space -> R 은, problem-specific knowledge 를 problem-independent way 로 표현한다.

best-first search 알고리즘은 general tree search 알고리즘의 인스턴스로, 가장 낮은 f(n) 값을 가지는 노드를 선택해 탐색한다. 이를 위해 f(n) 값을 오름차순으로 정렬하는 priority queue 이용한다.

만약 f(n) = h(n) 이면, greedy best-first search 라 부른다.

optimal 이 아닐 수 있다는 점에 유의하자.

루마니아 투어 문제를 다시 보자.

heuristic function 으로 straight line distance 를 이용했는데, 실제 거리와는 차이가 있다. (꼬불꼬불하니까)

A* algorithm

greedy best-first search 알고리즘은 쉽지만, 항상 optmial solution 를 돌려주지 않는다는 단점이 있다. 여기서 배울 A* algorithm 은 항상 optimal solution 을 찾아낸다.

h(n) 은 휴리스틱 펑션이고, g(n) 은 n 에 도달하기 까지의 비용이다. 그리고 이 두 함수를 이용해 만든 evaluation function f(n) 을 best-first search 에 적용해 최적의 해를 찾아낸다.

A* search is optimal if h(n) is admissible

A* search 를 이용해 Touring Romania 문제를 풀어보면

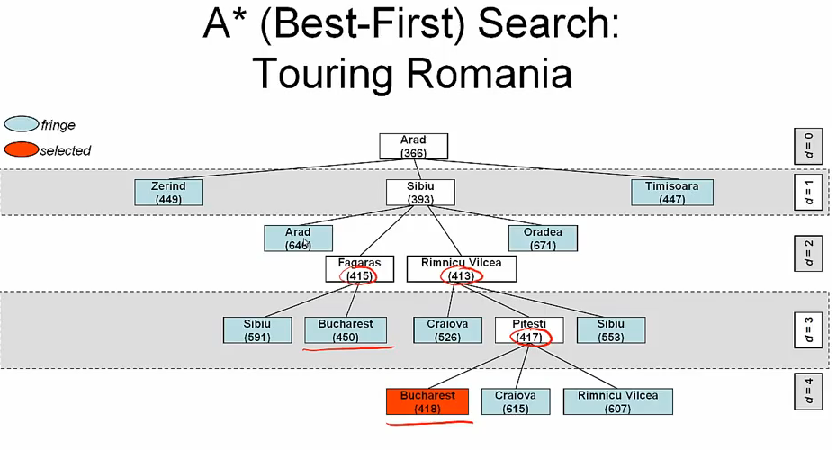
greedy best-first search 와 비교해보면 트리가 좀 더 큰데, 이건 A* search 가 일반적으로 좀 더 느리다는 사실을 보여준다.

8-puzzle 문제도 A* search 로 풀어보자. empty tile 을 옮긴다고 생각하고, cost function g(n) 은 모든 경우 1 로 볼 수 있다. 몇 가지 h(n) 을 생각해 볼 수 있는데,

Manhattan block distance 는 제 자리까지 얼마나 더 움직여야하는지를 의미한다.

Properties of A*

admissible 이란 말은, 항상 h(n) <= actual distance 임을 의미한다. f(n) = g(n) + h(n) 이므로, heuristic function 이 admissible 하면 가장 적은 f(n) 을 찾는 A* search 는 optimal solution 을 돌려준다.

A* search 는 complete 하다. 이는 탐색 과정에서 goal node 를 포함한 contour (윤곽, 등고선) 에 도달하기 때문이다. 여기서 contour 란 같은 비용으로 도달할 수 있는 sets of state 다. initial node 에서 시작해서 f-value 가 증가하는 방향으로 탐색이 이루어지므로 결국 꼭지점(goal) 에 도달한다. 사실 heuristics 이 없다면 A* search 는 다익스트라 알고리즘과 동일하다.

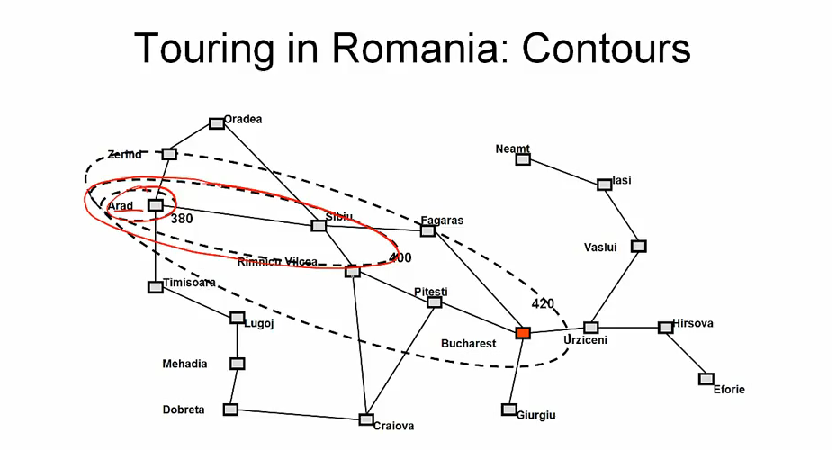
기하학적으로 보면 heuristic 이 더 정밀해질 수록 타원이 goal state 에 가깝게 넓어진다.

그리고 completeness 속성은, 거꾸로 말하면 optimal path 를 찾기 위해서 그보다 더 적은 cost 를 가지는 모든 path 를 탐색해야 함을 말한다.

A*star 알고리즘은 같은 heuristic 을 이용해, 가장 적은 수의 node 를 확장하면서 optimal solution 을 돌려준다. 만약 이보다 더 적은 node 를 확장하면서, optimal solution 을 돌려준다면 optmial solution 이 아닐 수 있다.

물론 효율성을 결정하는건 heuristic 의 연산 비용 등이 있겠지만, 적어도 node 수와 관련해서는 A* search 가 최적이다.

A* Graph Search

function aStarTreeSearch(problem, h)
  fringe <- priorityQueue(new searchNode(problem.initialState))
  allNodes <- hashTable(fringe)
  
  loop
    if empty(fringe) then return failure
    
    node <- selectFrom(fringe) // lowest f-value
    
    if problem.goalTest(node.state) then
      return pathTo(node)
      
    for successor in expand(problem, node)
      if not allNodes.contains(successor) then
        fringe <- fringe + successor @ f(successor) // g + h
        allNodes.add(successor)

여기서 fringe <- fringe + successor @ f(successor) 부분은 fringe 가 우선순위 큐이므로, 우선순위를 결정할 값으로 f-value 인 f(successor) 을 이용한다는 뜻이다.

그리고 if not allNodes.contains(successor) then 부분에서, 사실 노드를 두번째로 발견할 때 더 짧은 경로일 수 있으므로 비교하는 부분이 필요하다. 그러나 heuristic 이 admissible 하지 않으므로 A* search 가 최적해를 돌려주지 않을 수 있다.

최악의 경우 A* 알고리즘은 O(b) 의 time, space complexity 를 가진다. 여기서 b 는 branching factor 이란 뜻이다. 다시 말해서 exponential complexity 란 말이다.

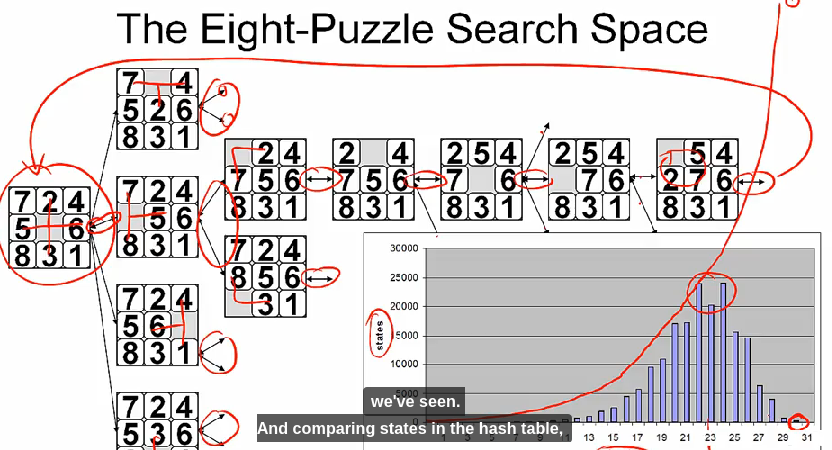
eight-puzzle 문제를 다시 보자.

그림에서 볼 수 있듯이, 빈 타일을 움직이다 보면 initial state 로 돌아올 수 있다. 만약 이 문제를 그래프로 표현하면 이미 방문한 노드를 다시 방문하고 있는지 해시테이블을 이용해 검사할 수 있다. 대신, 해시테이블을 만들고 사용하기 위한 비용이 든다.

반면 트리로 문제를 풀게되면, exponential 하게 search space 가 증가하기 때문에 worst case 에선 최적해를 찾기 위해 상당한 시간이 걸릴 수 있다.

한가지 더 생각해볼 문제는 permutation 이다.

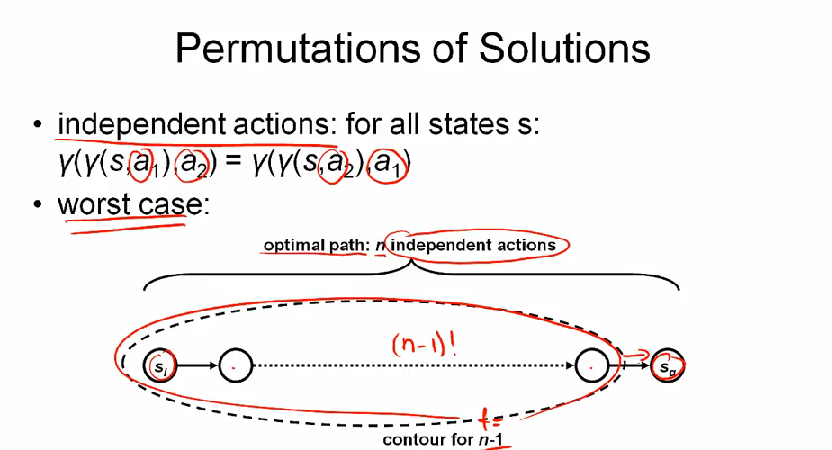
만약 모든 action 이 independent 하다면, solution 까지의 n action 중 n-1 contour 를 모두 방문해야 하므로 (n-1)! 의 성능이 나온다.

Good Heuristics

heuristics 이란 goal node 까지의 estimatied value 를 돌려주는 함수라고 기술적으로 정의할 수 있다.

• heuristics are criteria, methods, or principles for deciding which among several alternative courses of action promises to be the most effeictive in order to achieve some goal

그렇다면, 무엇이 good heuristics 일까?

평가해야할 state 를 줄이고, 적정 시간 내에 solution 을 찾을 수 있어야 한다. 간단할수록 정확도가 떨어지며, 정확할수록 복잡해진다. accuracy 와 관련해서는, 최적의 actions 을 찾아낸다는 보장은 없지만 good heuristics 이라면 그렇지 않은 것 보다 더 자주 best course of actions 를 찾을 수 있어야 한다.

• 문제가 주어졌을때, 어떻게 좋은 heuristics 을 찾아낼 수 있을까?
• 이 과정을 자동화 할 수 있을까?

heuristics 을 찾는 한 가지 방법은 relaxed problem 을 이용하는 것이다. original problem 에서 action 에 대한 restriction 을 좀 제거해서, 이에 대해 얻은 optimal solution 의 비용은 원본 문제에 대한 admissible and consistent heuristic 이다.

이는 restriction 이 제거되었기 때문에, 아무리 많아봐야 (at most) original problem 에 대한 cost 를 가지기 때문이다. 그러므로 admissible 하다. eight-puzzle 을 예로 들어보면 타일을 움직이는 action 에 대해 adjacent 또는 blank 조건을 버릴 수 있다.

지금까지 배운내용들을 좀 정리하면

• Heuristic funciton encodes problem specific knowledge in a problem-independent way by mapping a state to a real number. This information about search states can be used to make the search more efficient

• Greedy best-first search simply uses the heuristic function as the evaluation function. But better solution is provided by the A* algorithm. The evaluation function used by A* algorithm is simply the sum of the heuristic function for a node plus the cost of getting to thast node in the first place.

• A* is optimal. It does not expand more nodes than absolutely necessary. But A* is not the answer to all questions, specifically when it comes to graph search.

Summary

(1) heuristic function h: state space -> R 은 problem-specific knowledge 를 problem-independent way 로 표현한다. 여기서 h(n) 값은 노드 n 에서 goal 까지의 estimated cost 의 최소 값이다.

(2) best-first search 는 evaluation function 인 f 를 기준으로 f-value 를 정렬해 다음에 어떤 노드를 탐색할지 결정한다.

(3) 만약 f = h 이면 greedy best-first search 라 부른다.

(4) A* Search 는 evaluation function f(n) = h(n) + g(n) 을 이용한다. h(n) 은 heuristic function, g(n) 은 n 까지 도달하는 비용이다.

(5) 따라서 f(n) 은 n 을 통과하여 goal 까지 도달하는데 걸리는 cheapest solution 의 estimated cost 다.

(6) 만약 heuristic function h(n) 이 admissible 하면, 다시 말해 h(n) <= actual distance 이면 A* 는 optimal solution 을 돌려준다. 이는 f(n) = g(n) + h(n) 이기 때문이다.

(7) A* search 는 complete 하다. 이 말은 탐색과정에서 같은 비용으로 도달할 수 있는 모든 state 의 집합인 contour (등고선) 을 방문하면서 결국에는 goal node 를 찾는다는 뜻이다.

(8) 기하학적으로 보면 heuristic 이 정밀해질 수록 타원(등고선) 이 goal state 에 가깝게 넓어진다.

STRIPS

이제부터는 STRIPS 에 대해 알아보자. planning 의 본질은 원하는 goal 을 얻기 위한 action 을 결정하는 것이다. 즉, 시스템이 이런 결정을 내릴 수 있도록 해 주는 장치가 planner 인데, STRIPS 도 플래너다.

Wikipedia: STRIPS 에 의하면

In artificial intelligence, STRIPS (Stanford Research Institute Problem Solver) is an automated planner developed by Richard Fikes and Nils Nilsson in 1971 at SRI International. The same name was later used to refer to the formal language of the inputs to this planner. This language is the base for most of the languages for expressing automated planning problem instances in use today; such languages are commonly known as action languages.

STRIPS 는 어떤 action 을 사용할지를 결정하는 시스템이므로 representation 과 algorithm 이 필요하다.

Structured States

representation 의 일부인 state 에 대해 먼저 알아보자. state 에 access 할때는

• goal test
• applicable actions, successor states
• equality test, hash function
• heuristics estimate

이런 행동을 하려면 standardized 된 action state 의 표현 방법이 있어야 하는데, STRIPS repsentation 이 하는 일이 바로 이것이다.

먼저 object 를 정의하고, 이를 PDDL (Planning Domain Definition Language) 로 작성한다. robot 은 쉽게 오브젝트라 생각할 수 있지만 piles, pallet 은 떠오르지 않을 수 있다.

두 object 간 관계는 predicates 라 부른다.

여기서 ?l1, ?l2 등 물음표로 시작하는 것은 변수고 그 타입은 - location 처럼 뒤에 나온다. DWR-operators 링크에서 예제 PDDL 을 볼 수 있다.

우리가 작성한 language L 에는 많은 predicates, objects (constant symbols) 이 있지만, functional symbol 은 없다.

A state in a STRIPS planning domain is a set of ground atoms of L

여기서 atom 이란 a predicate 고, ground 하다는 것은 predicate 과 관련된 object 가 variable 이 아니고, 구체적인 인스턴스라는 뜻이다.

(1) ground atom p 가 state s 내에 있을때에만 p 가 참이다.

(2) literal 은 positive 일 수도 있고, negative 일 수도 있는 atom 이다. 이 때 ground literals g 내에 있는 모든 positive literal 이 s 내에 있고, g 내에 있는 모든 negative literal 이 s 내에 없으면 state s 는 ground literals g 를 만족시킨다.

Structured Operators

planning operators 는 name, pre-condition, effect 로 구성되는데, pre-cond 과 effect 는 literals 의 집합이다.

그리고 action 은 planning operator 의 ground instance 다.

쉽게 말해서 operator 는 variable 가 있는 predicate 의 집합이고, action 은 거기서 변수를 constant (실제 object) 로 치환한 것이다. operator 가 좀 더 generic 하다고 보면 이해하기 쉽다.

이 operator 를 PDDL 로 표현하면

이제까지 본 literals 를 이용해 applicable 한지, 그리고 어떻게 state transition 을 하는지 살펴보자.

L+, L- 를 각각 positive negative literals 이라고 하자.

action a state s 에 대해 a 의 pre-cond+ 가 s 에 있고, pre-cond- 가 s 에 없으면 applicable 하다.

그리고 applicable action 에 대해서 state transition r 는 state s 에서 a 의 effect- 를 빼고, 거기에 effect+ 를 합치는 것으로 정의한다.

• A 는 applicable actions 다. 초기에는 empty
• op 는 operator
• precs 는 remaining pre-cond
• 4번째 인자는 value 로 치환된 substitution 리스트다.
• s 는 state

먼저 precs+ 가 비었는지 검사하고, 무언가 있다면 pp positive pre-cond 를 뽑아내, propositions of state sp 에서 state s 를 하나씩 검사한다. 만약 substitution 이 valid 하면 재귀적으로 반복한다.

더 이상 precs+ 가 없으면 precs- 를 검사하면서, 만약 state 가 negative pre-cond np 를 만족하지 못하면, 리턴하고 모두 만족하면 variable 을 모두 치환하여 applicable action 리스트인 A 에 추가한다.

그림에서 왼쪽 케이스를 보면 로봇 r1 이 도착지점인 loc2 에 존재할 수 없기 때문에 not valid

Domains and Problems

classical planning 은 다음의 요소로 구성된다.

• task: find solution for planning prolem
• planning problem:

(1) initial state (atoms - relation, objects)
(2) planning domain (operators - name, prec, effects)
(3) goal

• solution (plan)

STRIPS 도 마찬가지로

따라서 STRIPS planning 문제는 planning domain, inital state, goal 로 구성된다.

DWR domain 간단예제를 좀 보자.

전체 문제는 여기로 DWR-pb1

지금까지 본 것은 planner 에게 주어야할 input 이었다. 이제 output 인 plan 이 무엇인지 보자.

State-Space Search

지금까지는 representation 에 대해 봤다. 지금부터는 STRIPS 에서 알고리즘을 어떻게 적용할지 알아보자. 기본적인 아이디어는

• search space is subset of state space
• nodes correspond to world states
• arcs correspond to state transitions
• path in the search space correspaonds to plan

따라서 standard search algorithm (e.g BFS, DFS, A*) 를 planning problem 에 적용할 수 있다. 좀 더 자세히 보자. state-space planning 을 search problem 으로 바꾸기 위해

initial state, goal, 을 정하고 path cost function 으로 action 의 길이를 사용한다. successor function 은

successor state 를 표시하기 위해 감마를 사용하고, 지수 위치에 있는 0, m 등은 몇번째 succssor 인지를 나타낸다. U 는 합집합, 유니온이다. 따라서 transitive closure 는 가능한 모든 합집합이다. (reachable states from initial state)

따라서 STRIPS planning problem 에서는 goal state S_g 와 reachable state 인 transitive closure 의 교집합이 empty 가 아니어야 솔루션이 존재한다.

Forward State-Space Search

function fwdSearch(O, s_i, g)
  state <- s_i
  plan <- <>
  
  loop
    if state.satisfies(g) then 
      return plan
    
    applicables <- {ground instance from O applicable in state}
    
    if applicable.isEmpty() then 
      return failure
    
    action <- applicable.chooseOne() ; non-deterministic
    state <- r(state, action)
    plan <- plan * <action> ; add action to plan

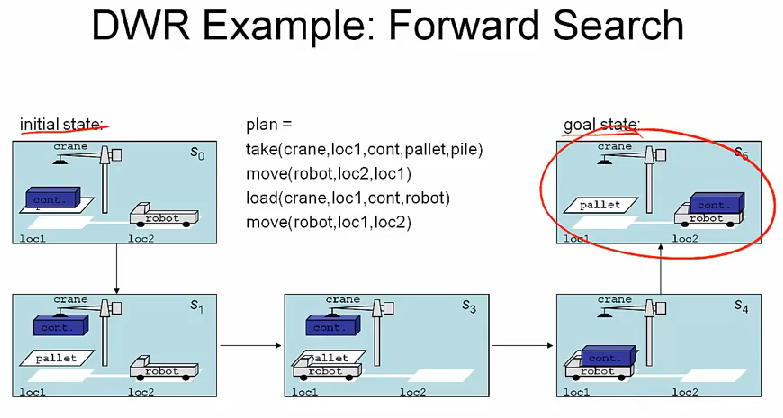
forward search 는 두가지 속성을 가지는데

• sound: if the function returns a plan as a solution then this plan is indeed a solution
• complete: if there exists solution plan then there is an execution trace of the function that will return this solution plan

Backward State-Space Search

backward search 는 intial state 부터 시작하는 것이 아니라 goal 부터 시작해서 거꾸로 진행하는 알고리즘이다. 먼저 relevant 와 regression set 의 개념부터 알아보자.

action a, goal state g 에 대해

• g 와 effect(a) 의 교집합이 empty 가 아니고
• g+ 와 effect-(a), g- 와 effect+(a) 의 교집합이 empty 이면

a is relevant for g

이 때 releavant action a 에 대해 g 의 regression set 은

r^(-1) (g, a) = (g - effect(a)) U precond(a) 로 정의한다. relavant action 의 effect 를 제거하고, 그의 pre-condition 을 넣으면 previous state 가 되기 때문이다. 예제를 좀 보면

(define (problem random-pbl1)
  (:domain random-domain)
  (:init
     (S B B) (S C B) (S A C)
     (R B B) (R C B))
  (:goal (and (S A A))))
  
(define (domain random-domain)
  (:requirements :strips)
  (:action op1
    :parameters (?x1 ?x2 ?x3)
    :precondition (and (S ?x1 ?x2) (R ?x3 ?x1))
    :effect (and (S ?x2 ?x1) (S ?x1 ?x3) (not (R ?x3 ?x1))))
  (:action op2
    :parameters (?x1 ?x2 ?x3)
    :precondition (and (S ?x3 ?x1) (R ?x2 ?x2))
    :effect (and (S ?x1 ?x3) (not (S ?x3 ?x1)))))  

여기서 relevant action 은 (op1 A A A), (op1 A A C), (op1 A B A) 다.

따라서 backward search 알고리즘을 이용하면, state-space planning 을 search problem 으로 바꿀때는

• initial state g
• goal test: s_i satisfies s
• path cost function: length of actions
• successor function: r^-1 (s)

예제를 좀 보자.

Summary

STRIPS 세션을 정리하면

• STRIPS representation provides a standardized way of representing the internal structure of states, namely a sets of ground atoms. So we have objects thar are related by some relations, and sets of these atoms describe what the world states look like.
• define interal structure of operators look like. negative effects, positive effects.
• define planning domains (initial, goal state), problem using PDDL
• to solve planning problem, we can use forward, backward search. Buy they are actually inefficient

따라서 다음시간엔 forward, backward 보다 더 효율적인 알고리즘을 배운다.

Refs

(1) Artificial Integelligence Planning, by Dr.Gerhard Wickler, Prof. Austin Tate
(2) xkcd image
(3) Wikipedia - STRIPS