AI Planning 1: Intro

planning 이란
- explicit deliberation process that chooses and organizes actions by anticipating their outcomes
- aims at acheving some pre-stated objecives
결국 AI planning 이란
computational study of this deliberation process
이런 관점에서 볼 때 AI planning 을 연구하는 이유는
scientific goal of AI: understand inteligence. planning is an important component of rational behaviour
engineering goal of AI: build intelligent entitie which are choosing and organizing actions for autonomous intelligent machines
planning 을 크게 domain-specific, domain-independent 로 분류할 수 있다.
- domain-specific planning: use specific representations and techniques adapted to each problem.
중요한 도메인으로 path and motion, perception, manipulation, commuication planning 등이 있다.
- domain-independent planning: use generic representations and techniques. exploit commonalities to all forms of planning. leads to general understanding of planning
domain-independent planning complements domain-specific planning
Conceptual Model for Planning
모델로 state-transition system 을 사용하는데, 이 시스템은 (S, A, E, r) 로 구성된다.
S = {s1, s2, ... }is a finite or recursively enumerable set of statesA = {a1, a2, ... }is a finite or recursively enumerable set of actionsE = {e1, e2, ... }is a finite or recursively enumerable set of eventsr: S x (A u E) -> 2^Sis a state trasition function- if
ainAandr(s, a)is not empty,ais applicable ins
state trasition function 은 상태 S 와 액션 A 또는 이벤트 E 를 받아, 가능한 모든 상태 2^S 를 만든다.
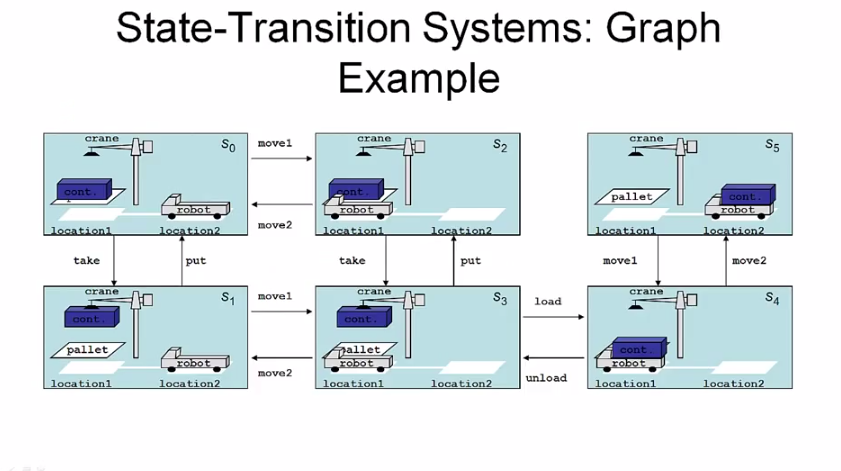
state trasition system 은 그래프를 이용해서 표현할 수 있다. G = (N, E) 에서 node N 은 상태를, edge E 는 state transition 을 나타낸다.
state trasition system 은 모든 가능한 상태를 표현하는 좋은 방법이다. 그러나 우리가 실제로 원하는건 plan 이다. 여기서 plan 이라 하면 주어진 특정 state 에서 시작해서, 원하는 objective 를 얻기까지의 action 을 말한다.
objective 는 조건을 만족하는 특정 상태 s 나, 상태의 집합이 될 수 있다.
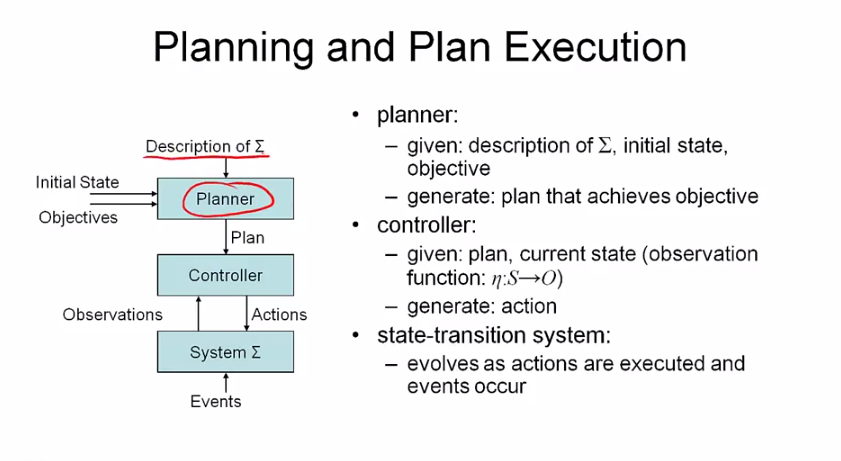
planning 문제를 풀기 위해 plan execution 을 이용하는 경우가 많다. planner 는 state transition system sigma 와 initial state, objectives 를 받아 plan 을 만들고, controller 가 이와 current state (observation) 을 받아 가능한 action 을 만든다. system 은 action 과 외부의 event 에 의해 변화한다.
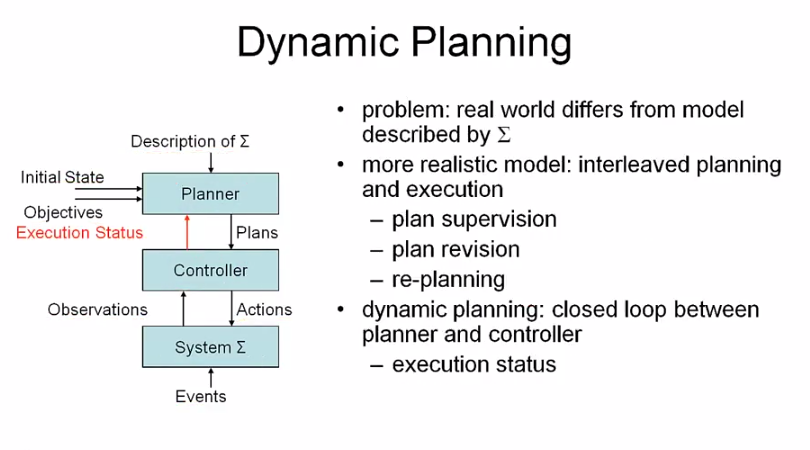
그러나 많은 경우 model 과 현실의 system 이 일치하지 않기 때문에, dynamic planning 이란 방법을 사용한다.
만약 controller 가 real system 과 model 이 다른 경우를 인식해서 planner 에게 execution status 를 넘겨주어 새로운 plan 을 만들도록 한다. 이걸 plan revision 이라 부른다.
Search Problem

search problem 의 4가지 요소는
- initial state
- successor function
- goal
- path cost

여기서 static 이란 말은 no-event 라는 뜻이다. implicit time 은 activity 의 duration 을 고려하지 않는다는 뜻이다.
Search Node

search problem 을 풀기 위한 알고리즘을 보기 전에, 어떻게 표현할 것인지를 먼저 이야기 하자. search node 의 구성 요소는
- state
- parent node
- action
- path cost
- depth
이제 general tree search algorithm 을 보면
function treeSearch(problem, strategy)
fringe <- { new searchNode(problem.initialState) }
loop
if empty(fringe) then return failure
node <- selectFrom(fringe, strategy)
if problem.goalTest(node.state) then
return pathTo(node)
fringe <- fringe + expand(problem, node)
여기서 problem 은 search problem 으로, 위에서 언급 했듯이 initial state, successor function, goal, path cost 를 포함한다.
fringe 는 아직 방문하지 않은 노드의 집합이고 마지막 부분에서 expand 함수는 successor function 을 적용해서 새로운 노드를 돌려준다. 이 과정을 fringe 가 비거나, 원하는 노드를 찾을때 까지 반복한다.
재밌는 사실은 search graph 가 유한하더라도 search tree 가 무한할 수 있다. 노드가 두개이면서 bi-directed 인 그래프를 생각해 보자.

위에서 본 strategy 는 successfor function 적용을 스케쥴링하는 요소다.
- selects the next node to be expanded from the fringe
- determines the order in which nodes are expanded
- aim: produce a goal state as quickly as possible
strategy 가 deterministic 이면, 알고리즘도 deterministic 이라 볼 수 있다. 반대로 strategy 가 없으면 non-deterministic 이다.
대부분의 search tree 는 상당히 크다. 요즘 나오는 컴퓨터 메모리에도 올리기 부담스러울 정도로. 따라서 strategy 가 메모리에 올라갈 tree 부분을 결정하고, 그에 따라 알고리즘이 실패할지, 성공할지를 결정하므로 매우 중요하다.
Example Problem
- Sliding-Block Puzzle (toy problem)
- N-Queens (toy problem)


Context

AI Planning, Coursera
그림의 윗 부분을 보면 AI planning 은 3가지 문제로부터 출발한 것을 볼 수 있다.
- Studies of Human Problem Solving
- Operations Research
- Theorem Proving



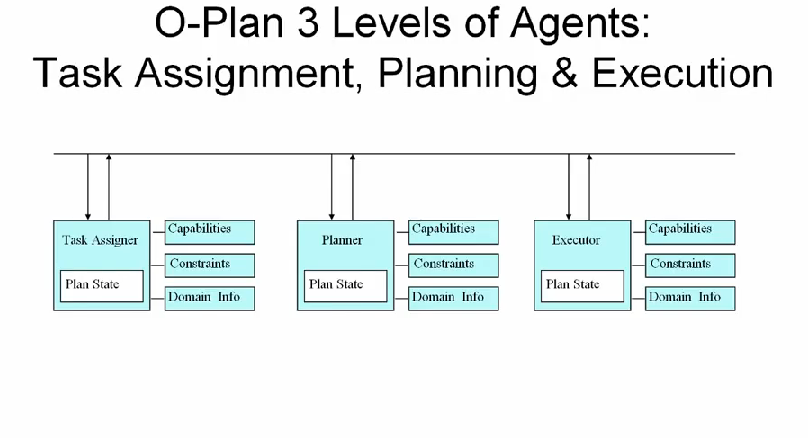
O-Plan 은 유닉스 시스템 어드민의 역할을 수행했다고 한다. 쉘 스크립트를 만들고, 볼륨을 삭제하거나 추가하는 등
practical AI planner 의 특징으로는
- hierarchical task network (HTN) planning
- partial order planning (POP)
- rich domain model
- detailed constraint mgmt, simuilations and analyses
- intergration with other systems (UI, DB, spreadsheets, etc)

Course Reading
(1) Review of AI Planners to 1990
Hendler, J.A., Tate, A. and Drummond, M. (1990) “AI Planning: Systems and Techniques”, AI Magazine Vol. 11, No. 2, pp.61-77, Summer 1990, AAAI Press.
(2) O-Plan Paper
Tate, A. and Dalton, J. (2003) “O-Plan: a Common Lisp Planning Web Service”, invited paper, in Proceedings of the International Lisp Conference 2003, October 12-25, 2003, New York, NY, USA, October 12-15, 2003. (4 pages)
Refs
(1) Planning Image
(2) AI Planning History Image
comments powered by Disqus