AI (CS188): Search
agent 가 good decision 을 내릴려면 planning 을 해야합니다. 그러기 위해선 어떤 action 이 좋을지 search (탐색) 해 보아야 하고 결국 풀어야 할 문제는 search problem 이 됩니다.
(1) reflex agent
- Choose action based on current percept (and maybe memory)
- May have memory or a model of the world’s current state
- Do not consider the future consequences of their action
- Consider how the world IS
자신이 인지하는 environment 에 기반하여 어떤 action 을 취할지 결정하나, action 의 결과를 고려하지 않고 결정을 내리기에 문제가 생길 수 있습니다. reflext agent 가 rational 할 수 있을까요?
Of course. Rationality is a function of the actions you take, not the computation. So if you had a big enough, good enough lookup table, and you’re taking the right actions. Rationality doesn’t care what process led to them. Reflex is a comment on the thought process
(2) planning agents
planning agent 는 reflex agent 와는 다르게 what if 를 질문합니다. 따라서
- Decisions based on (hypothesized) consequences of actions
- Must have a model of how the world evolves in response to actinos
- Must formulate a goal(test)
- Consider how the world WOULD BE
planning agent 는 action 을 선택할때 real world 에서 실제로 실행해보진 않습니다. 대신 model 을 이용해 simulation 을 해봅니다. 따라서 planning agent 에서는 real world 를 반드시 모델링 해야 합니다.
In order to have a planning agent, you must have a model of the world
그렇기 때문에 모델상에서 goal 인지 테스트 할 수 있는 방법도 필요합니다.
planning 과 관련해서 complete planning 과 optimal planning 이 있습니다. complete planning 은 solution 을 찾아내고, optimal planning 은 best solution 을 찾아냅니다.
또한 planning agent 는 한번에 plan 을 세워 실행할 수도 있지만, 매 실행 후 다시 re-planning 할 수도 있습니다.
Search Problem
search problem 은 다음처럼 구성됩니다.
- A state space: models how the world is
- A successor function (with actions, costs): models how it evolves in response to your actions
- A start state and a goal test
그리고 solution 은 start state 를 goal state 로 변환하는 a sequence of actions (a plan) 입니다.
다시 정리하자면, state 는 world 를 어떻게 모델링 하는지를 나타내고, successor function 은 action 에 world 가 어떻게 반응할지를 나타냅니다.

Search problems are just models
실제로 현실세계를 그대로 시뮬레이션하기엔 복잡하기때문에, 이를 계산하기 위해 rough 한 모델이 필요합니다. 이 model 적절하다면 search problem 의 결과도 정확합니다.
모델을 너무 추상화 해서 만들면 (abstract too much) 문제를 풀 수 없고, 그 반대라면 현실세계의 복잡함을 모두 다뤄야 하기 때문에 계산이 어려울 수 있습니다. 따라서 적절한 정도의 abstraction 이 필요합니다.
예를 들어 모든 dot 을 먹는 팩맨 에이전트를 만든다고 할때, state 에 문제를 풀기에 필요 이상의 정보를 넣으면 search space 가 너무 커져 계산이 어렵고, 너무 추상화해서 문제를 풀기에 필요한 정보가 부족하면 solution 을 찾는다 해도 올바른 solution 이 아닐 수 있습니다.
Search State Graph
state space graph 는 search problem 의 mathematical representation 입니다.
- Nodes are (abstracted) world configurations
- Arcs represent successors (action results)
- The goal test is a set of goal nodes (maybe only one)
- In a search graph, each state occurs only once
Search State Tree
search tree 는 plan 이 어떠할지를 나타내는 일종의 what if tree 입니다.
- The start state is the root node
- Children correspond to successors
- Nodes show states, but correspond to PLANS that achieve those states
- For most problems, we can never actually build the whole tree
general tree search 알고리즘은
function TREE-SEARCH(problem, strategy) returns a solution, or failure
initialize the search tree using the initial state of problem
loop do
if there are no candidates for expansion
then return failure
choose a leaf node for expansion according to strategy
if the node contains a goal state
then return the corresponding solution
else expand the node and
add the resulting nodes to the search tree
end
여기서 중요한 요소는 fringe (현재 고려중인 nodes), expansion, exploration strategy 다. 특히 어떤 fringe nodes 를 선택할 것인가가 중요한 질문이 됩니다.
널리 알려진 방법으로 Depth-First Serach, Breadth-First Search 등이 있습니다. 이들 search algorithm 의 성능을 평가하기 위해 다음 요소를 고려할 수 있습니다.
- complete: guaranteed to find a solution if one exists
- optimal: guaranteed to find the least cost path
- time complexity
- space complexity
그리고 DFS 은 branching factor b, depth m 이라 했을때
- At any given time during the search, the number of nodes on the fringe can be no larger than
b*m - The number of nodes expanded throughout the entire search can be as large as
b^m
BFS 알고리즘에서 branching factor b, depth s 라 했을때
- At any given time during the search, the number of nodes on the fringe can be large as
b^s - The number of nodes expanded throughout the entire search can be as large as
b^s
두 방법을 섞은 iterative deepening 이란 알고리즘도 있습니다. limit 1 까지는 DFS 를 돌려보고, 실패하면 limit2 까지 DFS 를 돌려보는 방식입니다.
Uniform Cost Search (UCS) 란 것도 있는데 priority queue 를 이용해서 더 낮은 cost 부터 탐색하는 방식입니다. UCS 는 complete, optimal search 입니다. 단점으로는
- Explores options in every direction
- No information about goal location
지금까지 배운 search algorithm 은 모두 uninformed search 입니다. 간단히 정리하면
- search operates over models of the world
- the agent doesn’t actually try all the plans out in the real world
- planning in all “in simulation”
- your search is only as good as your models
위에서 본 search algorithm 은 fringe strategies 만 다르고 모두 동일합니다. 개념상으로는 모든 fringes 는 priority queue 입니다. DFS 와 BFS 의 경우에는 각각 stack, queue 를 이용해서 priority queue 의 log(n) 오버헤드를 피할 수 있습니다.
Informed Search
이번시간에는 state 의 정보를 이용하는 informed search 와 graph search 를 배웁니다. informed search 의 기본적인 아이디어는 direction 을 결정할때, goal 에 가까운 방향인지를 알 수 있는 정보를 이용하는 것입니다.
(1) informed search
- heuristics
- greedy search
- A* search
(2) Graph Search
Search Heuristics
A heuristic is:
- A function that estimatees how close a state is to a goal
- Designed for a particular search problem
문제에 따라 heuristics 는 다릅니다. 루마니아 투어 문제의 경우 직선거리 가 될 수 있고, 팬케잌 문제(하노이탑) 의 경우 잘못 올려진 팬케잌의 수가 heuristic function 이 될 수 있습니다.
이런 heuristics 을 어떻게 알고리즘에 적용할까요? 하나는 DFS 처럼 같은 sibling 사이에서 더 낮은 heuristics 값을 가지는 fringe 를 선택하는 방법이 있습니다. 이걸 greedy search 라 부릅니다.
반면 BFS 처럼 같은 heuristics 값을 가지는 모든 fringe 를 탐색할 수도 있습니다. 이걸 A* search 라 부릅니다.
Greedy Search
greedy search 는 heuristic (estimate of distance to nearest goal for each state) 을 이용해서 fringe 를 선택하지만, DFS 처럼 badly-guided 될 수 있습니다. 항상 optimal 한 솔루션을 찾아주진 않는다는 이야기입니다.
A* Search
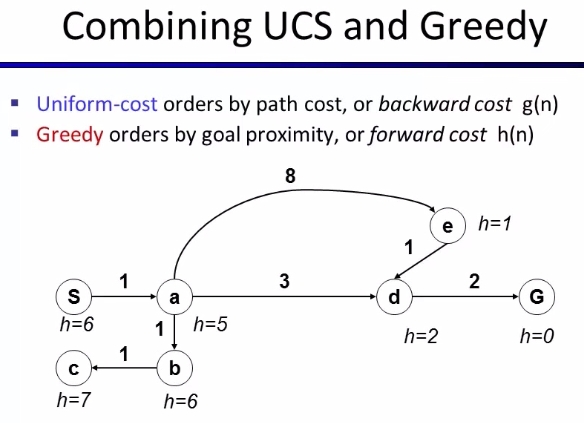
A* Search 는 f(n) = g(n) + h(n) 을 이용합니다. 즉, 지금까지 온 거리 g(n) 과 앞으로 남은 (예측) 거리 h(n) 을 더한 값을 이용해서 어떤 fringe 를 선택할지 결정합니다.
A* 와 관련해서 생각해 볼 한가지는 goal fringe 를 enqueue 할 때가 아니라 dequeue 할때 stop 해야한다는 것 입니다. 이는 현재 queue 에 있는 것중 goal 까지 더 작은 g(n) 을 가진 fringe 가 존재할 수 있기 때문이죠.
A* search 는 admissible 하면 optimal 입니다. 여기서 admissible (optimistic) 하다는 뜻은 heuristics 값 h(n)이 절대로 실제 cost h*(n) 보다 높지 않다는 뜻입니다. (always underestimate)
0 <= h(n) <= h*(n)
- Inadmissible (pessimistic) heuristics break optimality by trapping good plans on the fringe
- Admissible (optimistic) heuristics slow down bad plans but never outweigh true costs
uniform-cost search 와 A* search 를 기하학적으로 비교해보면, UCS 는 정원의 등고선을 그리며 goal 을 탐색하지만 A* 는 goal 쪽으로 기운 타원형태의 등고선이 만들어집니다.
정리하자면
- DFS, BFS: uninformed search, don’t consider cost
- UCS: uninformed search, only consider cost
- Greedy search: informed search, only consider heuristic
- A* search: informed search which uses both cost and heuristic
Admissible Heuristics
어려운 search problem 을 최적으로 풀어내려면 admissible heuristics 를 만들어야 하는데, 이 admissible heuristics 은 본래 문제에서 constaints 가 조금 줄어들어 새로운 action 을 사용할 수 있는 relaxed problem 의 솔루션이 될 수 있습니다.
그리고 inadmissible heuristic 도 때로는 유용할 수 있습니다. optimal solution 이 꼭 필요하지 않다면요.
그러나 이번에는 admissible heuristics 을 만드는 연습을 해보겠습니다. 8 puzzle 을 search problem 으로 해서요. 먼저 해야 할 질문은
- What are the states?
- How many states?
- What are actions?
- How many successor from the start state?
- What should the costs be?
(1) 만약 heuristic 을 number of tiles misplaced 로 한다면, 이건 admissible 일까요?
당연히 admissible heuristic 입니다. 왜냐하면 어느 action 도 한번에 1 개 이상의 타일을 옮길 수 없으니까요. 그런데 이건 relaxed problem heuristic 입니다. 최대 8 번만에 문제를 풀려면 타일을 직접 정확한 위치에 붙여야 합니다. 부직포 붙이듯이요.
(2) 만약 타일을 직접 목적지로 한번에 움직이진 않지만, 다른 타일을 무시하고 움직일 수 있다면 어떨까요? 아까보단 less relaxed 하다고 생각해봅시다. 이 경우 manhattan distance 를 이용할 수 있습니다. 이것도 마찬가지로 relaxed heuristic 이지만 아까보단 좀 덜 루즈합니다.
아까보다는 heuristic h 값이 더 커졌으니까, 가장 정확한 heuristic (actual cost) 값은 이것보다는 적어도 크다고 생각할 수 있습니다. 일종의 lower bound 라고 보면 쉽습니다.
그리고 heuristic 이 더 정확해졌기 때문에, expanded nodes 수도 이전보다 훨씬 줄어들게 됩니다.
(3) actual cost 를 heuristic 으로 사용하면 어떨까요? 이 값은 당연히 admissible 합니다. h(n) = h*(n) 이니까요. 게다가 expanded nodes 수도 가장 적습니다.
다만 문제는, 가장 정확한 heuristic 이기 때문에 매 턴마다 이 값을 계산하기 위한 연산 비용이 비쌉니다. 이것이 A* 알고리즘이 가진 trade-off 입니다. quality of estimate 와 work per node 를 적절히 조절해서 heuristic 을 만들어야 합니다.
As heuristics get closer to the true cost, you will expand fewer nodes but usually do more work per node to compute the heuristic itself
나침반을 보고 길을 찾을때, loose heuristic 은 좀 더 넓은 범위에서 맞다고 알려주어 이용하기 쉽다면, actual cost 의 경우에는 나침반이 제시하는 올바른 방향이 너무나 작기때문에 자세히 보고, 여러번봐야 하는것과 비슷합니다.
정리하자면 heuristic 이 actual cost 에 가깝다고 해서 반드시 좋은건 아닙니다. 연산시간을 고려하면 적정 수준의 loose heuristic 을 사용할 필요가 있습니다.

모든 heuristic 값이 더 크면 dominance 라고 말합니다. 다시 말해 더 정확한, actual cost 에 가깝다는 뜻입니다. 그리고 admissible 한 두 heuristics 에 대해 그 max 값도 당연히 admissible 합니다.
bottom lattice 를 zero heuristic, top 을 exact 라 부릅니다. 만약 zero heuristic 을 이용하면 uniform-cost search 와 동일합니다.
Graph Search
tree search 는 중복되는 부분에 대해 다시 탐색하므로 비효율적입니다. 이 부분을 개선하기 위해 모든 state 를 단 한번만 expand 할 수 있습니다. set of expanded states 를 유지하고, state 를 탐색하기 전에 이미 expanded 되었는지 검사하면 됩니다.
graph search 는 completeness 엔 문제가 없으나 not-optimal 일 수 있습니다. 아래 예제를 보면 sub-optimal solution 을 리턴합니다. admissible heuristic 임에도 불구하고요.
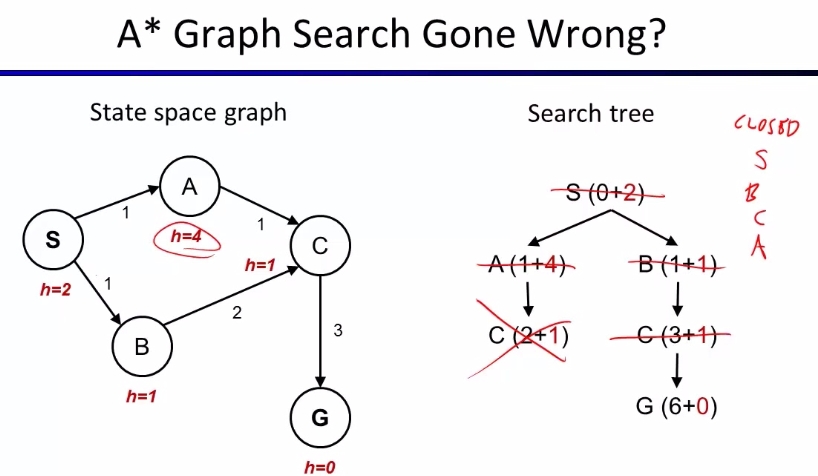

이건 consistency 속성이 만족되지 않아서 그렇습니다. goal 까지의 admissibility 뿐만 아니라, 각 arc 마다도 h <= actual cost 를 만족하면 consistent 하다고 말합니다. 만약 heuristic 이 consistent 하면 f value 가 절대로 줄지 않기 때문에 결과적으로 graph search 를 통한 결과도 optimal 이 됩니다.
- Fact 1: In tree search, A* expands nodes in increasing total f value (f-contours)
- Fact 2: For every state
s, nodes that reachsoptimally are expanded before nodes that reachssuboptimally
Optimality
(1) Tree Search
- 만약 heuristic 이 admissible 이면 A* 는 optimal 입니다
- UCS 는
h = 0인 special case 입니다
(2) Graph Search
- 만약 heuristic 이 consistent 이면, A* 는 optimal 입니다.
- UCS 도
h = 0이어서 consistent heuristic 이므로 optimal
Consistency implies admissibility
일반적으로 대부분의 natural admissible heuristic 는 consistent 합니다. 특히 relaxed problems 에서 나왔다면 더더욱요
Refs
(1) Artificial Integelligence (CS 188) by Dan Klein, Pieter Abbeel
(2) Title Image
comments powered by Disqus