Edit this page

Algorithm Algorithm: Union Find

Algorithm: Union Find

Union Find

Dynamic Connectivity

N 개의 오브젝트가 있을때,

Union command: connect two objects
Find/connected query: is there a path connecting the two objects?

이렇게 두 경로가 연결되어있는지 아닌지를 판별하는 알고리즘은 다양하게 활용될 수 있다.

Pixels in adigital photo
Computers in a network
Friends in a social network
Transistors in a computer chip

Modeling

connection 에서 몇개의 성질들을 뽑아낼 수 있는데,

Reflexive: p is connected to p
Symetric: if p is connected to q, then q is connected to p
Transitive: if p is connected to q and q is connected to r, then p is also connected to r
Connected Components: mamximum set of objects that are mutually connected

이제 연산들을 정의해 보면

Find query: Check if two objects are in the same component
Union command: Replace components containing two objects with their union

연산을 구현할때는 아래의 3가지 요소를 고려해야한다.

Number of objects N can be huge
Number of operations M can be huse
Find queries and union command may be intermixed

;; initialize union-find data structure with N objects (0 to N-1)
class UF(int N) 

;; add connection between p and q
void union(int p, int q)

;; are p and q in the same component?
boolean connected(int p, int q)

;; component identifier for p (0 to N-1)
int find(int p)

;; number of components
int count()

Quick-find

Dynamic Connectivity 를 푸는 한 방법으로 eager approache 를 사용하는 Quick-find 가 있다.

데이터 구조는 배열을 사용하며 int id[], 만약 p 와 q 가 연결되어있다면 똑같은 값을 가진다. 따라서

connected: p 와 q 가 같은 값을 가지는지 살핀다.
union: id[p] 와 같은 가지는 모든 인덱스의 값을 id[q] 로 바꾼다

구현은 다음과 같다.

// UnionFind.java
public interface UnionFind {
	public void union(int p, int q);
	public boolean connected(int p, int q);
}

// QuickFind.java
public class QuickFind implements UnionFind {
	
	private int[] id;
	
	public QuickFind(int N) {
		this.id = new int[N];
		
		for(int i = 0; i < this.id.length; i++) {
			this.id[i] = i;
		}
	}

	public void union(int p, int q) {
		if (!connected(p, q)) {
			int pValue = id[p];
			
			// replace id values same as p's into the value of q
			for(int i = 0; i < this.id.length; i++) {
				if (id[i] == pValue) {
					id[i] = id[q];
				}
			}
		}
	}

	public boolean connected(int p, int q) {
		return id[p] == id[q];
	}

}

// QuickFindTest.java
import static org.hamcrest.CoreMatchers.*;
import static org.junit.Assert.*;

import org.junit.Before;
import org.junit.Test;


public class QuickFindTest {
	
	private UnionFind uf;
	
	@Before
	public void setup() {
		uf = new QuickFind(10);
	}

	@Test
	public void testConnected() {
		assertThat(uf.connected(0, 1), is(false));
	}
	
	@Test
	public void testUnion() {
		assertThat(uf.connected(0, 1), is(not(true)));
		
		uf.union(0, 1);
		uf.union(0, 2);
		
		assertThat(uf.connected(0, 1), is(true));
		assertThat(uf.connected(1, 2), is(true));
	}
}

find(connected) 연산은 O(1), union 연산은 O(n) 의 복잡도를 가진다. 강좌에서는 각각 2 array accesses, at most 2N+1 array accesses 로 표현했다. 따라서 Quick-find 의 Cost Model 은 아래와 같다. (Order of growth of number of array accesses)

initialize: N
union: N
conncected: 1

이런 Quick-find 방법 문제점은 union 연산이 너무 비싸다는 것이다. N개의 오브젝트에 대해 N번의 Union 연산을 수행하면 N^2, 즉 Quadratic(제곱)의 비용이 드는데, 이건 큰 문제다.

Quadratic algorithms don’t scale with technology.

컴퓨터가 10배 빨라지고, 메모리도 10 배만큼 늘었다고 하자. quadratic algorithm 으로는 문제의 사이즈가 10배가 되면, 걸리는 시간은 100배가 된다. 연산 시간이 10배 빨라졌으므로 문제를 해결하려면 여전히 10배의 시간이 걸린다. 즉 기술이 10배나 발전해도, 문제의 사이즈에 해당하는 시간이 여전히 걸리는 것이다.

Quick-find 접근 법은, find 연산만 빠르다.

Quick-union

Quick-union 은 알고리즘 디자인적으로 lazy approach 라 볼 수 있다. Quick-find 와 같은 자료 구조(배열)을 사용하나 자료 구조에 대한 interpretation 이 다르다.

(http://www.timgittos.com/learning/princeton-algorithms-part-1/week-1/)

이 경우 연산은 각각 아래와 같이 생각할 수 있다.

find: Check if p and q have the same root
union: To mege components containing p and q, set the id of p’s root to the id of q’s root

구현은 아래와 같다.

// UnionFind.java
// same as above

// QuickUnion.java
public class QuickUnion implements UnionFind {
	
	private int[] id;
	
	public QuickUnion(int N) {
		this.id = new int[N];
		
		for(int i = 0; i < N; i++) {
			this.id[i] = i;
		}
	}
	
	public int getRoot(int n) {
		int root = id[n];
		
		while(root != id[root]) {
			root = id[root];
		}
		
		return root;
	}

	public void union(int p, int q) {
		if (!connected(p, q)) {
			int pRoot = this.getRoot(p);
			int qRoot = this.getRoot(q);
			id[pRoot] = qRoot;
		}
	}

	public boolean connected(int p, int q) {
		return getRoot(p) == getRoot(q);
	}
}

// QuickUnionTest.java
import static org.hamcrest.CoreMatchers.is;
import static org.hamcrest.CoreMatchers.not;
import static org.junit.Assert.assertThat;
import static org.mockito.Mockito.*;

import org.junit.Before;
import org.junit.Test;
import org.mockito.Mockito;

public class QuickUnionTest {
	
	UnionFind uf;

	@Before
	public void setup() {
		uf = new QuickFind(10);
	}
	
	@Test
	public void testGetRoot() {
		QuickUnion spy = Mockito.spy(new QuickUnion(5));
		
		assertThat(spy.getRoot(0), is(0));
		assertThat(spy.getRoot(1), is(1));
		assertThat(spy.getRoot(2), is(2));
		assertThat(spy.getRoot(3), is(3));
		assertThat(spy.getRoot(4), is(4));
		
		spy.union(0, 1);
		assertThat(spy.getRoot(0), is(1));
		assertThat(spy.getRoot(1), is(1));

		spy.union(2, 3);
		spy.union(4, 2);
		assertThat(spy.getRoot(2), is(3));
		assertThat(spy.getRoot(3), is(3));
		assertThat(spy.getRoot(4), is(3));
	}
	
	@Test
	public void testConnected() {
		// initial     : 0 1 2 3 4
		// union(0, 1) : 1 1 2 3 4
		// union(2, 3) : 1 1 3 3 4
		// union(3, 1) : 1 1 3 1 4
		
		//   1   4
		//  0 3
		//    2 
		
		QuickUnion spy = Mockito.spy(new QuickUnion(5)); 
		when(spy.getRoot(1)).thenReturn(1);
		when(spy.getRoot(0)).thenReturn(1);
		when(spy.getRoot(3)).thenReturn(1);
		when(spy.getRoot(2)).thenReturn(1);
		when(spy.getRoot(4)).thenReturn(4);
		
		assertThat(spy.connected(0, 4), is(not(true)));
		assertThat(spy.connected(1, 4), is(not(true)));
		assertThat(spy.connected(2, 4), is(not(true)));
		assertThat(spy.connected(3, 4), is(not(true)));
		
		assertThat(spy.connected(0, 1), is(true));
		assertThat(spy.connected(0, 2), is(true));
		assertThat(spy.connected(0, 3), is(true));
		assertThat(spy.connected(1, 2), is(true));
		assertThat(spy.connected(1, 3), is(true));
		assertThat(spy.connected(2, 3), is(true));
	}
	
	@Test
	public void testUnion() {
		QuickUnion spy = Mockito.spy(new QuickUnion(5));
		when(spy.getRoot(0)).thenReturn(0);
		when(spy.getRoot(1)).thenReturn(1);
		when(spy.getRoot(2)).thenReturn(2);
		when(spy.getRoot(3)).thenReturn(3);
		when(spy.getRoot(4)).thenReturn(4);
		
		spy.union(0, 1);
		when(spy.getRoot(0)).thenReturn(1);
		spy.union(2, 3);
		when(spy.getRoot(2)).thenReturn(3);
		spy.union(2, 0);
		when(spy.getRoot(2)).thenReturn(1);
		when(spy.getRoot(3)).thenReturn(1);
		
		verify(spy, times(1)).connected(0, 1);
		verify(spy, times(1)).connected(2, 3);
		Mockito.reset(spy);
		
		assertThat(spy.connected(0, 1), is(true));
		assertThat(spy.connected(2, 3), is(true));
		assertThat(spy.connected(2, 0), is(true));
		assertThat(spy.connected(1, 3), is(true));
		assertThat(spy.connected(0, 3), is(true));
	}	
}

이 경우 Cost Model 은 아래와 같다.

getRoot: depth of n array accesses. O(n) in worst case
connected: depth of q and p array accesses. O(n) in worst case
union: depth of q and p array accesses. O(n) in worse case

Quick-find 의 defect 는 - union is too expensive
- Trees are flat but too expensive keep them flat.

Quick-union 의 defect 는 - Trees can get tall
- find(connected) is too expensive (could be N array accesses)

Quick-union Improvement

1. Weighted Quick-union

기본 아이디어는 간단하다. union 연산을 수행할때 낮은 트리가 높은 트리에 속하게 함으로써 Worst case 를 방지하는 것이다. (마치 Balanced Tree 처럼)

(http://my.csdn.net/uploads/201206/12/1339479587_5986.png)

다른것은 모두 같지만, 트리의 크기를 비교해야 하기 때문에 트리의 크기를 저장할 배열이 필요하며, 이런 트리 크기를 비교하고 변경할 로직이 union 메소드에 추가되어야 한다.

// UnionFind.java is same as above
// QuickUnion.java is same as above
// WeightedQuickUnion.java

public class WeightedQuickUnion extends QuickUnion {
	
	int treeSize[];

	public WeightedQuickUnion(int N) {
		super(N);
		
		this.treeSize = new int[N];
		
		for(int i = 0; i < this.treeSize.length; i++)  {
			this.treeSize[i] = 1;
		}
	}
	
	// for debug
	public int getTreeSize(int index) {
		return treeSize[index];
	}
	
	@Override
	public void union(int p, int q) {
		if(!connected(p, q)) {
			int qRoot = getRoot(q);
			int pRoot = getRoot(p);
			
			if (treeSize[qRoot] >= treeSize[pRoot]) {
				id[pRoot] = qRoot;
				treeSize[qRoot] += treeSize[pRoot];
			} else {
				id[qRoot] = pRoot;
				treeSize[pRoot] += treeSize[qRoot];
			}
		
		}
	}
}

WeightedQuickUnionTest.java
import static org.hamcrest.CoreMatchers.*;
import static org.junit.Assert.*;

import org.junit.Test;
import org.mockito.Mockito;

public class WeightedQuickUnionTest {
	
	WeightedQuickUnionTest spy;

	@Test
	public void testUnion() {
		WeightedQuickUnion spy = Mockito.spy(new WeightedQuickUnion(5));
	
		assertThat(spy.connected(0, 1), is(not(true)));
		// 0 1 -> 1 1
		spy.union(0, 1);
		assertThat(spy.connected(1, 0), is(true));
		assertThat(spy.getTreeSize(0), is(1));
		assertThat(spy.getTreeSize(1), is(2));
		
		// 1 1 2 -> 1 1 1 
		spy.union(0, 2);
		assertThat(spy.connected(0, 1), is(true));
		assertThat(spy.connected(1, 2), is(true));
		assertThat(spy.connected(0, 2), is(true));
		
		assertThat(spy.getRoot(0), is(1));
		assertThat(spy.getRoot(1), is(1));
		assertThat(spy.getRoot(2), is(1));
		
		// 1 1 1 4 4
		spy.union(3, 4);
		assertThat(spy.connected(1, 3), is(false));
		assertThat(spy.connected(4, 3), is(true));
		
		// 1 1 1 4 1
		spy.union(2,  4);
		assertThat(spy.connected(4, 3), is(true));
		assertThat(spy.getRoot(4), is(1));
		assertThat(spy.getRoot(3), is(1));
	}
}

이 때 Cost Model 은

find: taks time proportional to depth of p and q O(logN)
union: take constant time, given roots (without roots O(logN))

같은 사이즈의 트리끼리 merged 도야 depth 가 1 깊어지므로 N개의 원소에 대해 Weighted Quick-union 이 구성하는 트리는 아무리 깊어봐야(at most) lg *N* 이다.

2. Path Compression

또 다른 Quick-union 개선 방안은, Path Compression 으로 루트를 탐색할때마다, 루트값을 새로 고쳐 써 다음번에 탐색할때 탐색 시간을 줄이는 방법이다.

// WeightedQuickUnion.java

...
...
	public int getRoot(int n) {
		
		int root = id[n];
		
		while(root != id[root]) {
			id[root] = id[id[root]];
			root = id[root];
		}
		
		return root;
	}
...
...

WQUPC(Weighted Quick-union with path compression) 은 iterated logarithm (lg**N*) 의 복잡도를 가진 다는 것이 증명 되었다. WQUPC 는 실제로 데이터를 읽어 들이는 비용도 있기 때문에 이론적으로는 linear 하지 않으나, 실제로는 linear 할 수 있다.

N 개의 오브젝트를 초기화 하고 여기에 대해 M 번의 union-find 연산을 수행한다면 Worst case 에 대해 복잡도를 정리해 보면

Quick-find: M * N
Quick-union: M * N
Weighted Quick-union: N + M logN (array 를 balanced 하게 만든다.)
Quick-union with path compression: N + M logN (array 를 flat 하게 만든다.)
WQUPC: N + M lg*N

이렇게 보면 알고리즘의 복잡도는 별거 없어보이는데, 사실 무지막지하게 큰 차이다. 10^9 개의 오브젝트에 대해서 10^9 연산을 할 경우 Quick-find 를 사용할때 30년이 걸린다면 WQUPC 는 6초만에 해결할 수 있다. 다시 말해, 알고리즘은 슈퍼컴퓨터도 별 도움이 되지 못하는 문제를 해결할 수 있다.

Applications of Union-find

Percolation
Dynmaic Connectivity
Lear common ancestor
Kruskal’s minimum spanning tree
and so on

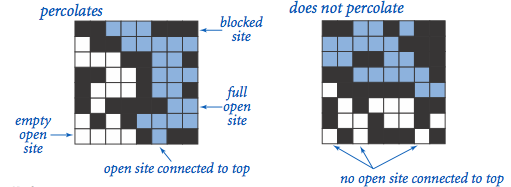
Percolation

(http://www.cs.princeton.edu/courses/archive/fall14/cos226/assignments/percolation.html)

Percolation 이란, N-by-N 의 Grid 에서 각 opened-site 는 확률 p blocked-site 는 1-p 의 확률을 가진다. 이 모델은 주로 물리 시스템을 모델링하기위해 사용된다.

이론상 N 이 충분히 크면

p > p* 인 지점에서는 almost certainly percolates 하고
p < p* 인 지점에서는 alomost certainly does not percolate 하다.

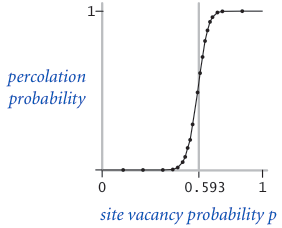(http://www.cs.princeton.edu/courses/archive/fall14/cos226/assignments/percolation.html)

문제는 그런 p* 값이 무엇이냐 하는건데, 수학적으로는 찾을 길이 없고, 컴퓨터 시뮬레이션으로는 Union-find algorithm 을 이용하면 구할 수 있다. 유명한 방법으로 Monte Carlo simulation 이 있는데, N-by-N Grid 를 blocked site 로 채우고, 랜덤하게 open site 를 만들면서 top 과 bottom 이 percolate 되는지 매번 확인한다. 연결되면, vacancy percentage 가 p* 에 대한 추정값이다.

구현 방법은 각 site 를 노드로 생각하고, top 과 bottom 을 그룹으로 묶어(virtual site) top 이 bottom 과 연결되는지 매번 체크하면 된다. 자세한 내용은 여기를 참조