Posted in Algorithm, coursera, intractability, P vs NP, NP completeness, search problem

Intractability

Thursday, January 01, 2015

Comment

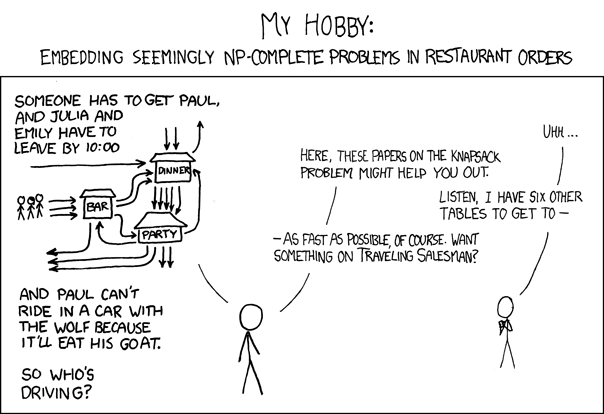
What is a general-purpose computer?
Are there limits on the power of digital computers?
Are there limits on the power of machines we can build?

컴퓨터 과학자들이 computation 에 관해 질문해 온 것들이다. 이 문제에 답하기 위해 computation model 을 좀 살펴보자.

긴 테이프가 있고, 기계는 테이프를 하나씩 읽어 0인지 1 인지 판별한다. 여기서 읽는것 뿐만 아니라 출력까지 가능하면 turing machine 이 된다. 일종의 universal computation model 이다.

(http://physics.kenyon.edu)

근데 놀랍게도 이것보다 더 진보한 연산 모델이 있느냐? 라는 질문에 대해 없음 이란 연구 결과가 나왔다고 한다.

Church-Turing thesis:

Turing machines can compute any function that can be computed by a physically harnessable process of the natural world.

여기서 thesis 인 이유는 증명이 아니기 때문이다. mathmatical theorem (정리) 가 아니다. 결국 이것이 의미하는 바는

No need to seek more powerful machines or languages
Enables rigorous study of computation (in this universe)
Turing machine is a simple and universal model of computation

Church-Turing thesis 에 대해 80 년동안이나 반례가 발견되지 않았다. 그리고 수 많은 computation model 이 발견되었지만 모두 turing machine 과 동일한 것으로 밝혀졌다. (lambda caculus, URM, SKI 등)

일반적으로 useful algorithm 이란 모든종류의 입력 에 대해 polynomial time aN^b 시간 내에 풀 수 있는 것을 useful algorithm 이라 말한다.

polynomial time 알고리즘은 대부분 작은 a, b 를 가지기 때문에 다양한 문제로 적용하는것도 가능하다. 그러나 a, b 가 큰 경우 풀수 없는것과 마찬가지 일때도 있다.

Exponential growth dwarfs technological change

유용하지 않은 알고리즘의 예로, N 지점에 대한 TSP 는 brute force 를 이용하면 N! 이다.

얼마나 유용하지 않은가를 좀 더 생각해보자. 만들 수 있는 가장 큰 병렬 슈퍼컴퓨터를 가정 해보면

Suppose you have a giant parallel computing device
With as many processors as eletron in the universe
And each processor has power of today's supercomputers
ANd each processor works for the life of the universe

1000 도시의 TSP 를 brute force 로 풀려면, 이 병렬 슈퍼컴퓨터를 우주의 일생동안 돌려도 불가능하다.

1000! > 10^1000 > 10^79 * 10^13 * 10^17

이런 이유에서 어떤 문제가 polynomial time 내에 풀 수 없으면 intractable 하다고 말한다.

결국 우리가 풀 수 있는 문제는 poly-time algorithm 이 있는 경우이며, 어떤 문제가 이런 poly-time algorithm 을 가질까? 그건 쉽지 않다. 연구중이라고 함.

연구된 바로는 두 종류의 문제가 exponential time 일 것으로 본다.

Given a constant-size program, does it half it at most K steps? (input size = c + lgK)
Given N-by-N checkers board position, can the first player foce a win?

Four fundamental problems

(1) LSOLVE: Given a system of linear equations, find a solution

가우시안 소거법으로 N-by-N 시스템에서 N^3 시간 안에 해결된다.

(2) LP: Given a system of linear inequalities, find a solution

Ellipsoid 알고리즘을 이용하면 poly-time

(3) ILP: Given a system of linear inequalties, find 0-1 solution

no poly-time algorithm known. 있을거 같긴 한데 모른다고 함

(4) SAT: Given a system of boolean equations, find a binary solution

no poly-time algorithm known 이것도 있을거 같긴 한데 모른다고 함

Search Problems

Given an instance I of a problem, find a solution S or report none exists

답이 있거나, 없음을 말해줘야 하는데 이를 위해서 효율적으로 (poly-time) S 가 정답인지 검사할 수 있어야 한다.

위에서 본 LSOLVE, LP, ILP, SAT 문제 같은 경우 정답이 있으면 대입해서 poly-time 내에 검증할 수 있으므로 search problem 이다.

factor problem 도 search problem 이다. 주어진 n 비트 정수에 대해서, nontrivial factor 인지 아닌지는 나눠보면 되니까.

즉 search problem 에서는 답을 누군가 제공할때 그것이 답인지 아닌지를 poly-time 으로 검사할수 있냐 없냐가 중요하다.

NP

NP: is the class of all search problems. (class definition limits NP to yes-no problem)

앞에서 본 LSOLVE, LP, ILP, SAT, FACTOR 모두 NP 다.

P: is the class of search problems solvable in poly-time

LSOLVE, LP, SORT, STCONN 의 문제는 모두 P 다.

즉 답을 poly-time 내에 검증이 가능하면 NP 고, 거기에 답을 poly-time 내에 찾는것이 가능하면 P 란 이야기. P 가 중요한 이유는, 현실적으로 계산 가능한 문제이기 때문이다.

이론적으로는 1010401 * N ^(10^23) 도 계산 가능하다고 본다. ~~음!?!~~

Nondeterminism

Nondeterministic machine can guess the desired solution

regex 의 패턴매칭을 구현할때 했었던 NFA 처럼 일종의 nondeterministic machine 이 있다 하고, 이 기계가 답을 찾아준다고 하자. 예를 들면 이런 느낌이다.

int[] a = new int[N];

자바에선 0 으로 초기화 되는데, nondeterministic machine 을 이용하면 답으로 초기화 해주는 것이다.

DFA 를 NFA 로 바꾸었듯이, 같은 입력에 대해 다수의 상태를 가지도록 함으로써 튜링 머신(이하 TM) 도 쉽게 nondeterministic 로 만들 수 있다.

그러면 이제 NP 가 의미하는 바를 확실히 이해할 수 있다. nondeterministic polynomial time, 다시 말해 search problem 이 nondeterministic TM 위에서 poly-time 내에 풀 수 있다는 것이다.

(1) nondeterministic TM 이 답을 제공한다
(2) search problem 은 poly-time 내에 답인지 아닌지 판별이 가능하다.

조금 더 이해를 위해 위키를 인용하면

P는 결정론적 튜링 기계를 사용해 다항 시간 내에 답을 구할 수 있는 문제의 집합이고, NP는 비결정론적 튜링 기계를 사용해 다항 시간 내에 답을 구할 수 있는 문제의 집합이다. 여기에서 결정론적 튜링 기계에 사용한 프로그램을 비결정론적 튜링 기계에 적용할 수 있으므로, P는 NP의 부분집합이 된다. 하지만 여기에서 P와 NP가 같은 집합인지, 아니면 P가 NP의 진부분집합인지는 아직 밝혀지지 않았다. 현재 2000년에 클레이 수학연구소가 100만 달러를 걸었다.

Extended Church-Turing Thesis

이제까지 나온바를 정리하면

NP: search problems solvable in poly-time on a nondetermimistic TM

그리고 extended Church-Turing thesis 에 의하면

P: search problems solvable in poly-time in the natural world

따라서

To make future computers more efficient, suffices to focus on impoving implementation of existing design

P vs NP

P = NP 일까? 이게 사실이라면, search problem 에서 exponential time 의 brute force 방법을 사용하지 않아도 된다. poly-time 알고리즘이 있다는 이야기니까.

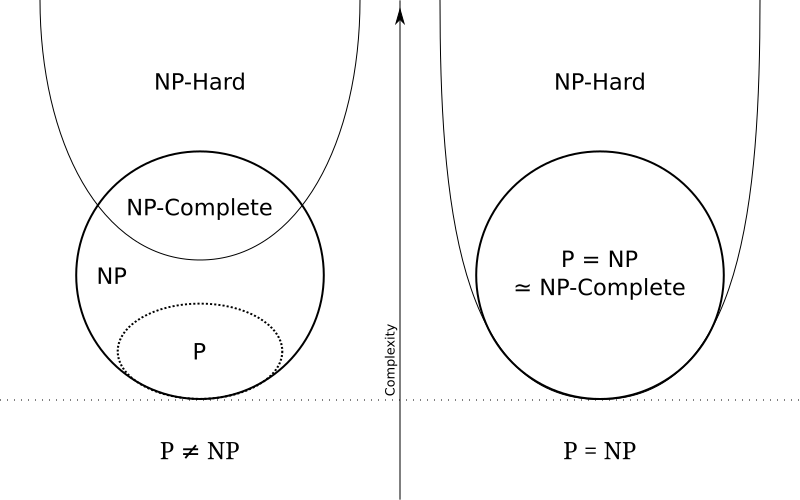
(http://commons.wikimedia.org/)

P = NP 일 경우 nondeterministic TM 이 별 도움이 안된단 이야기고, P != NP 일 경우,

If no, Would learn something fundamental about our universe

대부분의 학자들은 P != NP 라 믿는다. 이는 non-deterministic TM 이 이전까지 우리가 사용했던 머신보다 더 강력하기 때문이라고 한다. 즉, 문제를 해결하기 위해 필요한 머신의 성능이 훨씬 좋아야 하므로 NP 가 P 와 같진 않을거라는 이야기

Classifying Problems

SAT problem: Given a system fo boolean equations, find a solution

n 변수의 SAT 문제를 exhausitve search 로 풀면, 2^n 의 모든 경우를 다 시도 해봐야 한다. 더 빠른, poly-time 알고리즘으로 풀수는 없을까?

슬프게도 많은 학자들이 연구해 왔지만, 아직까지 발견되지 않았고 대부분의 학자들이 SAT 문제가 NP 라는 것에 동의한다. 증명되지 않았으므로 일종의 가정인데, 이 가정을 이용해 reduction 을 해 보자. 그럼 intractable 한 알고리즘을 찾아낼 수 있다.

Problem X poly-time reduces to problem Y If X can be solved with:

Polynomial number of standard computational steps

Polynomial number of calls to Y

따라서 SAT 를 문제 Y 로 poly-time reduction 가능하면, Y 는 (거의) intractable 이다.

If X cannot be solved in poly-time, then Y connot be solved in *poly-time
If Y can be solved in poly-time, then so can X

NP-Completeness

An NP problem is NP-complete if all problems in NP poly-time reduce to it

즉 모든 NP 문제가 어떤 문제 A 로 poly-time reduction 이 되면 A 는 NP-complete 라는건데, Cook, 1971 에 의해 SAT 가 NP-complete 임이 증명되었다.

증명을 간단히 요약하면

Convert non-deterministic TM notation to SAT notation
If you can solve SAT, you can solve any problem in NP

일종의 reduction 이다.SAT 인스턴스를 poly-time 으로 풀면 non-deterministic TM 문제로 풀 수 있는 NP 문제도 poly-time 으로 풀수 있게된다.

SAT 를 poly-time 으로 풀면 P = NP
NP 문제에 대해 poly-time 알고리즘이 없으면 SAT 에 대해서도 없다.

많은 문제가 NP-complete 다.

Coping With Intractability

암호학 같은 경우 intractability 가 널리 쓰인다. RSA 의 경우

To use: multiply two n-bit integers (poly-time)
To break: factor a 2 n-bit integer (unlikely poly-time)

근데 1994년에 양자 컴퓨터로는 n 비트 FACTOR 문제가 n^3 안에 풀릴 수 있다는 가설이 제기되었다. 그럼 실 세계에서는 P 만 poly-time 으로 풀린다는 extended Church-Turing thesis 는..

아무튼 intractability 를 해결하기 위해서 쓸 수 있는 몇 가지 테크닉이 있다.

(1) Solve arbitrary instances of the problem

specialc cases 는 tractable 일 수 있다. 예를 들어 2-SAT 은 linear time 이다.

(2) Solve the problem to optimality

heuristic 을 이용해 알고리즘을 만드는 방법도 있다. 최적은 아니지만 좋은 결과를 낼 수도 있기 때문이다. (TSP assigment heuristics)

그리고 대부분 좋은 결과를 돌려주는 approximation algorithm 을 이용할 수도 있다. MAX-3SAT 은 87.5% 는 보장한다고 함.

(3) Solve the problem in poly-time

Complexity theory deals with worst case behavior

Hamilton path

해밀턴 경로의 경우 모든 정점을 한번씩 방문해야 하는데, NP-complete 문제라고 한다. 오일러 경로(edge) 는 쉽다고 함.

exponential time 으로 구현할 수 있다. 일반 DFS 와 다른점은 clean up 부분.

public class HamiltonPath  
{
    private boolean[] marked; // vertices on current path
    private int count = 0; // number of Hamiltonian paths

    public HamiltonPath(Graph G)
    {
        marked = new boolean[G.V()];
        for (int v = 0; v < G.V(); v++)
            dfs(G, v, 1);
    }

    //depth is the length of current path (depth of recursion)
    private void dfs(Graph G, int v, int depth)
    {
        marked[v] = true;
        if (depth == G.V()) count++;
        for (int w : G.adj(v))
            if (!marked[w]) dfs(G, w, depth+1); //backtrack if w is already part of path
        marked[v] = false; // clean up
    }
}

Summary

P: Class of search problems solvable in poly-time
NP: Clas of all search problems, some of which seem wickedly hard
NP-complete: Hardest problems in NP
Intractable: Problem with no poly-time algorithm
A poly-time algorithm for an NP-complete problem would be a stunning breakthrough (a proof that P = NP)
You will confront NP-complete problems in your career
Safe yo assume that P != NP and that such problem are intractable
Identify these situations and proceed accordingly

References

(1) Algorithms: Part 2 by Robert Sedgewick
(2) http://introcs.cs.princeton.edu
(3) Lecture note: intractability
(4) xkcd image
(5) Turing machine image
(6) Wikipedia: P-NP 문제

Old Lisper

Functional Programming World