Null space of a matrix is a vector space

standard geneartor 를 이용해서 f(x) = M * x 에서의 M 의 컬럼을 알아낼 수 있다.

어떤 함수 f 가 M * x 형태로 정의되면, f 는 linear function 이다.

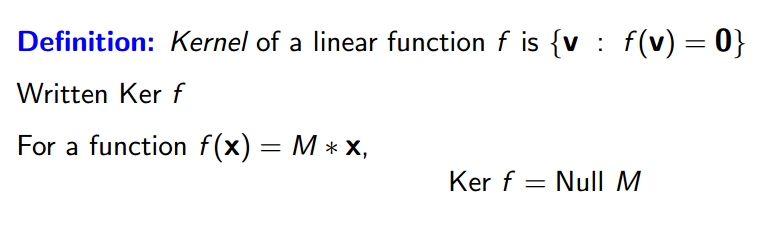
어떤 함수 f 의 kernel 은 image 를 0 으로 하는 집합이다. 다시 말해서 f(x) = M * x 에 대해 null matrix x 이 kernel

linear function f is one-to-one iff its kernel is a trivial vector space

위에 나온 속성은 상당히 중요하다. 왜냐하면 trivial kernel 이면, 다시 말해서 null matrix 가 trivial 이면, f 의 image b 는 아무리 많아봐야 하나이기 때문이다.

image 가 entire co-domain 과 같으면 onto 다.

두 matrix-vector function 의 composition 은 위처럼 쉽게 증명 가능하다. AB * x 로

이걸 이용하면 matrix-matrix multiplication 의 associativity 도 쉽게 증명 가능하다. (AB)C = A(BC)

Invertible

두 함수가 inverse 관계면 두 매트릭스도 inverse 관계다. 그리고 한 매트릭스의 inverse matrix 가 존재하면 invertible 또는 singular 라 부르며, 아무리 많아봐야 하나의 inverse 만 가진다.

invertible matrix 가 중요한 이유는, invertible matrix 가 존재하면 f 도 invertible 이고, 그 말은 f 가 one-to-one, onto 라는 소리다. 따라서 f(u) = b 에 대해 적어도 하나의 솔루션이 존재하고 (onto), 아무리 많아봐야 하나의 솔루션이 존재한다는 뜻이다 (one-to-one)

함수처럼 매트릭스도 A, B 가 invertible 일때만 AB 도 그러하다.

AB 에 대해 A, B 가 서로의 inverse 면 AB 는 identity matrix 지만 그 역은 성립하지 않는다.

위 그림의 A 에서 볼 수 있듯이 null space 가 trivial 하지 않기 때문에 one to one 이 아니어서 A 는 invertible 이 아니다.

AB, BA 가 모두 identity matrix 여야 A, B 가 서로 inverse 다.

매트릭스 M 이 one-to-one 인지는 trivial kernel 인지를 판별하면 된다. f(x) = M * x 는 linear function 이기 때문에 trivial kernel 이면 M 도 one-to-one 이다.

onto 인지는 어떻게 알 수 있을까?

Summary

지금 까지의 내용을 정리하면

1. u1 이 a * x = b 의 솔루션일때, V 를 a * x = 0 의 솔루션 셋이라 하면, u1 + V 는 a * x = b 의 솔루션 셋이다. 다시 말해서 V 는 null matrix
2. f(x) 가 M * x 형태로 나타낼 수 있으면 linear function 이다.
3. trivial kernel 이면 linear function f 는 one-to-one 이고, linear function f 가 one-to-one 이면 trivial kernel 을 가진다.

Refs

(1) Title image
(2) Coding the Matrix by Philip Klein