Linear Combinations

b 와 v1, ..., vn 이 주어졌을때

• a1, ..., an 을 찾을 수 있을까요?
• 있다면 unique solution 인지 어떻게 알 수 있을까요?

Span

• The set of all linear combinations of some vectors v1, ..., vn is called span of these vector

이브가 만약 위와 같은식을 만족한다는 사실을 알고 있다면, 패스워드의 모든 span {a1, ..., an} 에 대해서 적절한 response 를 추출할 수 있습니다. 증명은 위처럼 간단합니다.

Let V be a set of vectors if v1, ..., vn are vectors such that V = Span {v1, ..., vn} then

• we say {v1, ..., vn} is a generating set for V
• we refer to the vectors v1, ..., vn as generators for V

[x, y, z] = x[1,0,0] + y[0,1,0] + z[0,0,1] 을 R^3 의 standard generator 라 부릅니다.

Geometry of Sets of Vectors

• Span of the empty set: just the origin, Zero-dimensional
• Span {[1,2], [3,4]}: all points in the plane, Two-dimensional
• Span {[1,0,1.65], [0,1,1]} is a plain in three dimensions

k 벡터의 span 은 k-dimensional 일까요? 아닙니다.

• Span {[0, 0]} 은 zero-dimensional 입니다.
• Span {[1,3], [2,6]} 은 one-dimensional 입니다.
• Span {[1,0,0], [0,1,0], [1,1,0]} 은 two-dimensional 입니다.

그러면 어떤 벡터 v 가 있을때 dimensionality 를 어떻게 알아낼 수 있을까요?

위 그림에서 볼 수 있듯이 origin 을 포함하는 geometry object 를 표현하는 방법은 두가지 입니다. 각각은 나름의 쓰임새가 있습니다.

(1) span of some vectors
(2) 우변이 0 인 linear equation system 의 집합

field 의 서브셋은 3가지 속성을 만족합니다. field 를 R 이라 하면

• subset contains the zero vector
• if subset contains v then it contains av for every scala a
• if subset contains u and v then it contains u+v

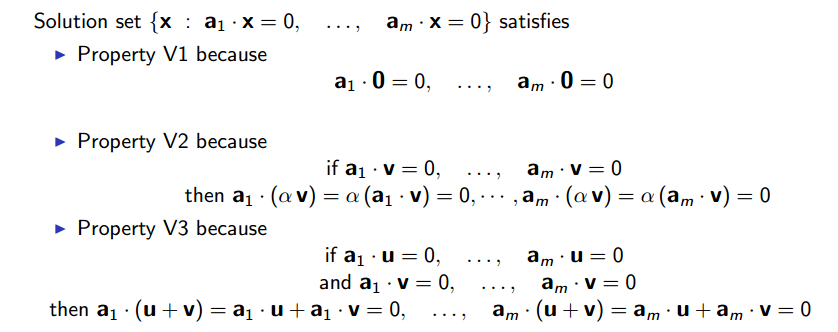
F^D 의 세가지 속성을 만족하는 subset 을 vector space 라 부릅니다. 그리고 U 가 vector space 고 vector space V 의 subset 일때, U 를 V 의 subspace 라 부릅니다.

뒤에서 배울테지만 모든 R^D 의 subspace 는 span {v1, ..., vn} 과 {x: a1 * x = 0, ..., an * x = 0} 의 형태로 쓸 수 있습니다.

우리는 벡터에 대해 sequence 나, function 을 정의하지 않았습니다. 단순한 operator 와 공리를 만족하는지, 그리고 property V1, V2, V3 정도만 따졌습니다. 벡터에 대한 이런 추상적 접근은 많은 장점이 있습니다. 그러나 이 수업에서는 사용하지 않겠습니다.

Vector Space

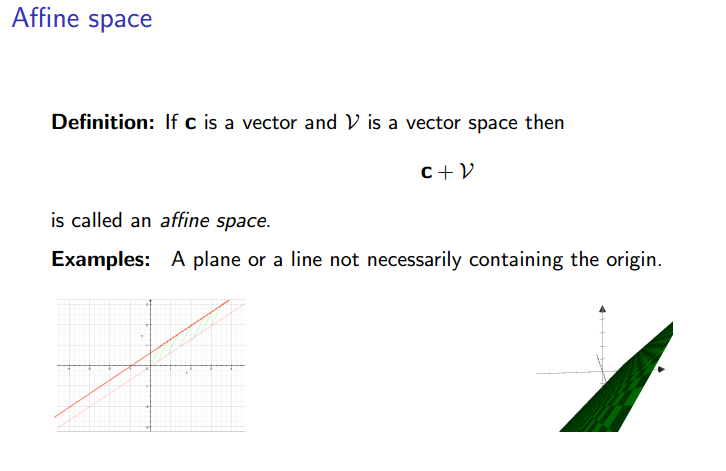
벡터 c 와 벡터 스페이스 V 에 대해 c + V 와 같은 형태를 affine space 라 부릅니다.

u1, u2, u3 를 담고있는 plain 을 u1 + V 형태로 표현하고 싶습니다. 어떻게 해야할까요?

V 를 span {a, b} 라 하고 a = u2 - u1, b = u3 - u1 라 하면 u1 + V 는 plain 의 변환이지만, 그 자체로서 plain 입니다

• span {a, b} 는 0 을 포함하므로 u1 + span {a, b} 는 u1 를
• span {a, b} 는 u2 - u1 도 을 포함하므로 u1 + span {a, b} 는 u2 를
• span {a, b} 는 u3 - u1 도 을 포함하므로 u1 + span {a, b} 는 u3 를 포함합니다.

따라서 u1 + span {a, b} 는 u1, u2, u3 를 모두 포함하는 평면입니다.

더 간단히 ru1 + au2 + bu3 (r + a + b = 1) 로 affine combination 을 표현할 수 있습니다. 그리고 더 formal 하게 정의하면,

affine space 를 a solution set of a system of linear equations 으로 표현할 수 있습니다. 그런데, 역으로 이 솔루션이 affine space 일까요?

반례를 하나 들어보면 1x = 1, 2x = 1 일때 솔루션은 없습니다. 그러나 벡터 스페이스 V 는 zero vector 를 가져야 하므로 affine space u + V 는 적어도 하나의 vector 는 가져아합니다. 모순이 발생합니다.

• Theorem: solution set of a linear system 은 empty 거나 affine space 입니다. 증명은 아래와 같습니다.

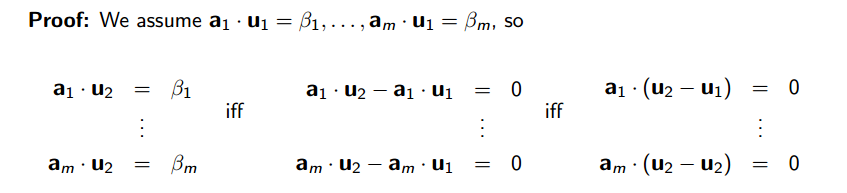
지금까지 증명한 것은, u1 이 linear system 의 솔루션일때, u1 + v (v in V) 도 솔루션이란 사실입니다. 여기서 V 는 homogeneous linear system 입니다. (우변이 0 인)

따라서

• unique solution 을 가질때는 V 가 0 을 해로 가질 때이고
• GF(2) 의 솔루션 수는 0 이거나, V 와 같습니다.

Checksum function

corrupted 파일이 올바른 파일로 인식될 경우는 오리지널 바이너리 p 에 대해 손상된 파일 p+e 가 위 슬라이드의 방정식을 만족할 경우입니다.

이 확률은 모든 가능한 n 벡터에 대해 존재하는 솔루션의 수 이므로 굉장히 낮습니다.

Refs

(1) Title image
(2) Coding the Matrix by Philip Klein