Algorithm Design and Analysis: Dijkstra, Heap, Red-Black Tree

Design and Analysis: Dijkstra, Heap, Red-Black Tree

Dijkstra’s Shortest-Path Algorithm

BFS 는 undirected graph 에서 최단 경로를 찾지만, 이건 모든 edge 의 길이가 1일때만 그렇다.

다익스트라(dijkstra, 데이크스트라) 알고리즘은 directed graph 에서 non-negative length 에 대한 최단 경로를 찾아낼 수 있다.

각 edge 가 음수라면, 모든 수에 특정 수를 더해 양수로 만들어도, 아니면 음수 그 자체로 다익스트라 알고리즘을 돌려도 최단 경로를 찾지 못한다. 다음의 그래프가 한 예다.

1 -> 2 // length: 1
2 -> 3 // length: -6
1 -> 3 // length: -2

금융거래를 보면 특정 거래를 edge 라 보고 대해 여기에 대하 이득과 손실을 각각 양수, 음수의 가중치를 가지는 그래프라 생각할 수 있는데, 여기엔 음수 가중치가 있으므로 다익스트라 알고리즘을 쓸 수 없다.

벨만 포드 알고리즘을 써야한다.

길이가 n 인 edge 를 길이가 1 인 n 개의 edge 로 늘려 BFS 를 쓸 수 없느냐 질문할 수도 있겠는데, 가중치가 상당히 크면 연산이 비효율적이 된다. (e.g 150000)

Algorithm

사실 다익스트라 알고리즘은 방문한 점 v 와 방문하지 않은 점 w 에 대해 edge (v -> w) 를 고르는 문제다. l_vw 를 v -> w 의 거리라 하고 A[v] 를 시작점 부터 v 까지의 최단거리라 하면 A[v] + l_vw 를 최소로 하는 edge 를 고르면 된다.

알고리즘은 이렇다. 시작점을 s 라 하면

X = {s} // vertices process so far
A = [s] // computed shortest path distances

// V is not visited vertices set  

while X != V
  // v in X, w not in X
  // select the edge minimizing [A]v + l_vw
  pick (v, w) 
  X + w
  A[w] = A[v] + l_vw

Correctness

다익스트라 알고리즘이 non-negative edge length 를 가진 directed graph 에 대해 최단경로를 찾아낸다는 것을 증명하자.

A 를 다익스트라 알고리즘이 찾아 낸 경로, L 을 실제 최단거리라 할 때 A[w*] = L[w*] 임을 보이면 된다.

귀납법을 이용해 먼저 가설을 세우면

Inductive hypothesis: all previous iterations correct

base case 인 시작점 s 에 대해 참임을 보이면 A[s] = L[s] = 0 이다.

현재 iteration 에서 찾아낸 edge 를 v* -> w* 라 하면, A[w*] = L[v*] + l_v*w* 이다.

이 때 그래프 안에 있는 모든 s -> w* 의 경로의 길이가 L[v*] + l_v*w* 보다 큼을 보이면 된다.

그래프 내에 있는 s -> w* 의 모든 경로 p 는 다음 형태를 가진다.

s -> y | -> z -> w*

여기서 s, y 는 방문한 점이고 z, w* 는 방문하지 않은 점이다.

s -> y | -> z -> w* 에 대해 p 의 길이는 다음 3개를 더한 것이다.

(1) l_sy >= A[y] = L[y] (by induction hypothesis)
(2) l_yz
(3) l_zw >= 0

즉, 모든 경로 p 의 길이 l_sy + l_yz + l_zw* 는 L[y] + l_yz 보다 크다.

그런데, 다익스트라 알고리즘으로 고른 경로 A[v*] + l_v*w* 는 L[y] + l_yz 보다 작거나 같다. 왜냐하면 A[v*], L[y], l_v*w* 는 최단경로인데, l_yz 는 최단경로일 수도, 아닐수도 있다.

따라서 우리 알고리즘으로 구한 거리가, 모든 경로 p 의 lower bound 보다 작거나 같다.

Running time

naive implementation 의 성능은 O(mn) 이다. n - 1 의 모든 vertex 를 살펴봐야 하고, 루프 내에서 러프하게 모든 edge 를 검사한다고 보면 된다.

다익스트라 알고리즘은 O(n) 정도까지 개선할 수 있다. 알고리즘의 변경이 아니라, 자료구조를 heap 으로 변경함으로써! heap 은 extract-min 연산에 대해 O(log n) 이다.

힙의 구조나 특성은 뒤에서 알아보기로 하고, 여기선 다익스트라 알고리즘에 어떻게 적용할지를 논의하자.

(1) heap 내부 원소들은 방문하지 않은 원소들의 집합 V - X 라 하자. X 는 방문한 원소들의 집합.
(2) V - X 내의 원소 v 에 대해서 key[v] 는 edge (u, v) 에 대한 다익스트라 알고리즘의 스코어다. (u 는 방문한 점)

따라서 v 의 키 값은 X 와 V - X 의 crossing edge u -> v 중에서 가장 작은 edge 길이다.

이때 X 내에 있지 않은 점 v 를 X 로 옮기면서 v -> w 로 새로운 crossing edge 가 생기고, 이로인해 w 의 key 값이 변할 수 있다. 이를 해결하기 위한 key 업데이트 로직은

// v is extracted from heap and added to X
for each edge (v, w)
  if w in heap
    delete w from heap
    recompute key[w] = min(key[w], A[v] + l_vw)
    reinsert w into heap

running time 은 heap operation 의 수로 결정되는데 각 연산 O(log n) 을

(1) n - 1 extract min -> n
(2) 그리고 edge 중심으로 보면, (v, w) 이 edge 가 재 계산될때는 v 가 X 에 추가될때다. 그 이후에는 (v, w) 는 crossing edge 가 되므로 delete, insertion 연산과 관련이 없어진다. 다시 말해 한 edge 당 at most one insertion and deletion 이 있다. -> m

따라서 heap operation 수는 O(n + m) 이다. 그런데, path 자체는 weakly connected undirected graph 이므로 m ~= n 이고 O(m + n) = O(m) 이라 볼 수 있다.

결국 힙을 이용한 다익스트라 알고리즘은 O(m log n) 이다. 이건 O(m * n) 보다 어마어마하게 빠르다.

What data structure should I use?

위 예제에서도 봤듯이, 적절한 데이터 구조의 사용은 알고리즘의 성능을 개선하는데 도움이 된다.

익히 아는 리스트, 큐 부터 시작해서 bloom filter, union find 등이 있는데, 이렇게 다양한 자료구조가 있는 이유는 우리가 하려는 task 가 다양하기 때문이다.

많은 데이터 구조중 무엇을 선택해야 할까? rule of thumb 는

Choose the “minimal” data structure that supports all the operations that need.

내게 필요한 것 이상의 과도한 연산을 제공하는 자료구조를 사용할 필욘 없다. 복잡한 연산이 있을수록, 자료구조는 더 복잡해지기 마련이다.

Heap

자료구조에서 가장 먼저 생각해야 할 것은 “어떤 operation 을 제공하는가?”, “running time 은 얼마인가?” 다.

Heap 은 key 를 가진 *object*를 위한 container 다. employer records, network edges, event manager 등에 이용할 수 있다.

힙의 기본 연산은 insert 와 extract-min (or max) 연산이다. 이 연산의 러닝타임은 O(log n) 이다. n 은 힙 내에 있는 오브젝트의 수다.

n 개의 batch insertion 에 대해 heapify 는 O(n), 임의의 원소를 제거하는 delete 는 O(log n) 이다. 정리하면

(1) insertion: O(log n)
(2) extract-min (or max): O(log n)
(3) heapify (batch): O(n)
(4) remove (arbitrary): O(n)

Application

힙을 어디에 쓸까? 먼저 생각해 볼 수 있는건 min value 가 연속적으로 필요한 작업에 쓸 수 있다.

(1) heap sort 는 힙에서 지속적으로 min-value 를 뽑아내서 정렬하는 방법이다. O(n logn) 의 성능을 보여준다. 이건 merge sort 나 randomized quick-sort 만큼 빠르다.

잠깐 생각해 볼 거리가 있다. quicksort 챕터에서 언급 했듯이 comparison-based sorting 은 O(n logn) 보다 더 빠를 수 없다. 힙 또한 비교를 이용해 정렬을 하므로 이보다 좋은 성능을 내기는 어렵다.

(2) 아까 힙을 event manager 에도 이용할 수 있고 했는데, priority queue 가 바로 그것이다. 각 게임 이벤트가 큐에 들어있다고 하면 여기서 key 는 각 event 의 발생시간이다. 다시 말해 발생시간이 먼저인 이벤트가 먼저 발생되도록 큐를 이용할 수 있다.

(3) median maintanence 에도 힙을 이용할 수 있다. x1, x2, ..., xn 의 배열에 대해 i 번째 스텝에서는 x1, ..., xi 의 중앙값을 돌려주는 문제다. O(i) 로 하면 정말 쉽지만, 조건이 하나 있다. 바로 O(log i) 의 퍼포먼스를 내야하는것. 어떻게 할까?

두개의 힙을 이용하면 쉽게 풀 수 있다. 데이터를 절반씩 나누어 max heap, min heap 각각에 나눠 담으면 된다. 그러면 각 힙의 루트가 중앙값이 될 수 있다.

(4) 마지막으로 힙은 다익스트라 알고리즘의 성능을 개선하는데 사용할 수 있다. 위에서 보았듯이 O(m logn) 의 퍼포먼스를 보여준다.

Implementation Details

힙을 배열 또는 트리로 보는 관점이 있는데, 여기선 쉬운 이해를 위해 트리로 설명한다. rooted, binary, as complete as possible tree 로 보면 된다.

(http://en.wikipedia.org/wiki/Binary_heap)

min heap 을 예로 들면, 부모는 항상 자식보다 작거나 같다. 따라서 루트는 모든 원소중 가장 작은 값을 가진다.

힙을 배열로 구현한다고 하자. 인덱스가 1부터 시작할때 parent(i) 는 i 가 짝수면 i/2, 홀수면 [i/2] 가 될 것이다. 자식을 구하는건 더 쉽다. i * 2 와 i * 2 + 1 이다.

insert 의 구현을 생각해 보자. 힙은 가능한 complete tree 기 때문에, 위 그림에서 새로운 숫자가 입력했을때 새로 생길 노드의 위치는 19 의 왼쪽 자식이다.

이렇게 완전 이진트리를 만드는 위치에 새로운 값을 삽입하고, 부모와 값을 비교해 가면서 값의 위치를 올려간다. 이 방법을 bubble-up 이라 부른다. 정리하면,

(1) stick k at end of last level
(2) bubble-up k until heap property is restored

extract-min 연산은 루트에 있는 수를 뽑아낸다. 이 위치에 마지막 노드를 넣고, bubble-down 함으로써 구현할 수 있다. 새롭게 루트가 된 노드를 내려가는 과정에서 왼쪽 자식, 오른쪽 자식과 모두 비교하여 가장 작은 수를 새로운 부모로 만들면 된다. 정리하면

(1) delete root
(2) move last leaf to be new root
(3) iterlatively bubble-down until heap property has been restored

이 두 연산은 이진트리의 n 번째 깊이까지 내려갈 수 있으므로 퍼포먼스는 O(log_2 n) 이다.

Balanced Search Tree

sorted array 에 대한 연산을 먼저 생각해 보자. 이로부터 balanced search tree 로 이끌어 낼 수 있는 연산들이 있을테다. 참고로 sorted array 는 static 이기 때문에 insertion, deletion 이 없다.

(1) Search: O(logn)
(2) Select: O(1) (given order statistic i)
(3) Min / Max: O(1)
(4) Predecessor / Successor: O(1)
(5) Rank: O(logn)
(6) Output in sorted order: O(n)

여기서 주어진 데이터가 몇 번째 데이터인지를 찾는 rank 는 search 와 똑같은 문제다. binary search 처럼 찾아가면서, 인덱스를 찾아내면 되기 때문이다.

이제 balanced search tree 를 생각해보자.

(1) Search: O(logn)
(2*) Select: O(logn)
(3*) Min / Max: O(logn)
(4*) Predecessor / Successor: O(logn)
(5) Rank: O(logn)
(6) Output in sorted order: O(n)
(7+) Insert: O(logn)
(8+) Delete: O(logn)

sorted array 에 비해 select, min or max, pred or succ 연산이 O(logn) 이 되었고 insert, delete 연산이 새롭게 추가됐다. 쉽게 기억하려면 sorted array + logarithmic insert, delete 라 생각하면 된다.

힙과 비교해보면, 두 자료구조 모두 insert, delete 를 O(logn) 이란 빠른 시간에 제공한다. 차이점은, 힙은 min or max 둘 중 하나만 매우 빠르게 제공한다는 것이다. 따라서 priority queue, scheduler 같은 기능을 구현한다면 balanced search tree 보단 힙이 더 좋은 선택이다.

Binary Search Tree

binary search tree 를 쉽게 기억하는 방법은 dynamic sorted array 라 기억하는 것이다. sorted array 가 제공하는 풍부하고 빠른 연산에 insert, delete 를 추가한 것이 바로 binary search tree, BST 다.

힙이 vertically sorted 라면 BST 는 horizontally sorted 다. 즉 왼쪽자식은 부모보다 항상 작고, 우측 자식은 부모보다 항상 크다.

(http://en.wikipedia.org/)

이런 구조적 특성때문에 search (탐색) 을 O(logn) 으로 빠른 시간 내에 해낼 수 있다. 근데, 최악의 경우 노드가 일렬로 주-욱 이어져 있다면 O(n) 의 퍼포먼스를 보여준다.

(http://epaperpress.com)

Implementation

이제 연산의 구현을 좀 생각해 보자.

(1) insert, search 는 비슷하다. 자신의 자리를 찾아 내려가다가, 해당 원소가 있으면 돌려주고 아니면 NULL 을 돌려주는 방법으로 search 를 구현할 수 있다. insert 도 값을 비교하면서 내려가다가 적절한 자리에 삽입하면 된다.

(2) max, min 연산은 가장 좌측 노드, 가장 우측 노드를 돌려줌으로써 쉽게 구할 수 있다.

(3) pred, succ 은 자신 다음으로 적거나, 자신 다음으로 큰 원소를 돌려주는 연산인데, 자신 기준으로 왼쪽 부트리에서 가장 우측에 있는 노드, 그리고 자신 기준으로 우측 부트리에서 가장 좌측에 있는 노드를 돌려주면 된다.

(4) in-order traversal 연산은 노드를 오름차순 순서로 방문하는 연산이다. 이것 역시 쉽게 구현할 수 있는데

let r = root of search tree

recurse left sub-tree
print current node
recurse right sub-tree

노드당 한번만 출력하므로, 퍼포먼스는 O(n) 이다

(5) delete 는 조금 복잡한데 3가지 경우를 고려해야 한다.

자식이 없을 경우
왼쪽 또는 오른쪽 자식만 있을 경우
양쪽 자식이 다 있을 경우

앞의 두 가지 경우는 어렵지 않은데, 양쪽 자식이 다 있을 경우는 조금 까다롭다. 이 경우는 지우려는 노드의 successor 나 predecessor 을 l 이라 하자. 지우려는 노드와 l 을 뒤 바꾸면, 이전 l 자리에 있던 노드는 left 또는 right 자식이 없으므로 하나의 자식만 있는 알고리즘을 이용해 제거하면 된다.

(http://commons.wikimedia.org/)

(6) select, rank 연산은 트리에 추가적인 정보를 기록함으로써 쉽게 구할 수 있다. 각 트리마다 자기를 포함한 자식들의 노드 수를 저장하면 된다.

(http://www.tcs.auckland.ac.nz/~georgy/)

매 삭제와 삽입 연산마다 각 트리의 사이즈를 변경해야 하는데 어렵지 않다. 삽입이나 삭제시 마지막 노드 혹은 predecessor, successor 를 찾아가면서 매번 노드를 방문해야 하므로 이 때 마다 새롭게 값을 변경하면 된다.

select, rank 알고리즘은

start at root x
let y = left sub-tree
let z = right sub-tree
let a = size of y

if a = i - 1 return x
if a >= i, recurse y, i'th statistic
if a < i, recurse z, (i - a - 1)'th statistic

러닝타임은 O(height) 다.

Red-Black Tree

이진트리는 운이 나쁠경우 O(n) 의 연산 성능이 나오기 나온다. 따라서 트리의 높이를 최대 O(logn) 으로 제한해 연산 성능을 개선할 수 있다.

이렇게 구조적인 제한을 이용해 성능을 개선하는 트리는 red-black tree 이외에도 AVL tree, splay tree, B tree 등이 있다.

Invariants

red-black tree 는 다음의 제약 조건을 제외하면 이진트리와 동일하다.

(1) each node is red or black
(2) root is black
(3) no 2 reds in a row -> red node has only black children
(4) every root - NULL path has same number of black nodes

여기서 (4) 는 unsuccessful search 를 생각하면 쉽다. 검색이 제대로 되지 않았을 경우 NULL 에서 중단하는데, 그때 까지의 모든 블랙 노드의 수가 다른 unsuccessful search 가 방문한 블랙 노드 수와 동일하다는 것이다.

(http://en.wikipedia.org)

예제를 통해 좀 살펴보자. 1 -> 2 -> 3 의 이진트리가 있을 때, 2 가 레드 노드라 하자. 그러면 규칙 (4) 를 위반한다. unsuccessful search 의 경우인 0 과 4 를 찾을때 블랙 노드의 개수가 다르다.

Height Guarantee

위에서 언급한 제약조건이 실제로는 트리의 높이를 height <= 2 log_2(n + 1) 로 보장한다.

우선 살펴봐야 할 것은, 모든 root-null 경로가 >= k 인 노드를 가지고 있다면, 그 트리는 k 깊이 까지는 완전 이진트리다.

If every root-null path has >= k nodes, then tree includes (at the top) a perfectly balanced search tree of depth k - 1

이 것은 레드블랙트리만이 아니라 모든 이진트리에 적용된다. 이제 전체 노드 n 과 관계를 살펴 보자.

이진트리이므로 노드의 수 n >= 2^k - 1 과 k 에 대해 k <= log_2 (n+1) 이다.

아까 k 는 root-null 경로의 노드의 수 라고 했었다. 그리고 레드블랙트리의 (3), (4) 조건을 다시 생각해보면

(3) no 2 reds in a row -> red node has only black children
(4) every root - NULL path has same number of black nodes

레드 블랙트리에서 모든 노드가 블랙이면, (4) 에 의해서 root-null 경로의 블랙 노드가 최대이므로 블랙 노드의 upper bound 는 <= log_2 (n+1) 이다. 그리고 레드 블랙 트리에서 root-null 경로의 노드수가 깊이가 되므로 이때의 높이는 log_2 (n+1) 이다.

다른 경우를 생각해 보자. 레드블랙트리의 root-null 경로에는 중간 중간 레드 노드가 낄 수 있는데, 레드 노드가 최대로 끼어있을때는 (3) 조건에 의해 블랙노드만큼이다. 이 때 블랙노드는 upper bound 에 의해 <= log_2 (n+1) 이므로, 레드노드도 최대 <= log_2 (n+1) 이다.

따라서 레드블랙트리의 깊이는 최대 <= 2 * log_2 (n + )1 이므로, 연산에 대해 O(log n) 을 보장한다.

Rotation

이진트리의 삽입, 삭제 연산은 레드블랙트리에서의 제약조건을 망가트릴 수 있다. 따라서 삭제와 삽입 연산에 부가적으로 구조를 유지하기 위한 작업이 필요하다.

레드블랙트리 뿐만 아니라 AVL tree 나 다른 balanced search tree 도 구조를 유지해야 하는데, 여기에 공통적으로 사용하는 연산이 rotation 이다. 한번 알아보자.

Idea: locally rebalance sub-trees at a node in O(1) time.

먼저 left roation 만 생각하자. 다음 그림에서 우측에 있는 트리를 좌측처럼 변경하는 것이다. P 가 Q 의 자식이 되도록 하는것이다.

(http://en.wikipedia.org/wiki/Tree_rotation)

여기서 B 의 원소는 P 보단 크고 Q 보다 작다. 따라서 Q 와 P 의 위치를 변경하면 B 는 P 의 오른쪽에 와야 한다. 이것이 left rotation 이다. 경로를 따라 왼쪽으로 한칸씩 밀려갔다고 생각하면 기억하기 쉽다.

right rotation 은 이것을 정확히 반대로 수행하면 된다. 좌측에 있는 트리에서 P, Q 를 경로를 따라 하나씩 우측으로 밀고, B 는 C 의 왼쪽으로 이동하면 된다.

모든 연산은 포인터 변경으로 끝나므로 O(1) 이다.

Insertion

이제 rotation 을 이용해 red-black tree 에서 삽입 연산을 구현해 보자. 삽입과 삭제의 기본적인 아이디어는

(1) 이진트리에서의 insert / remove 연산을 수행 한다.
(2) 레드, 블랙을 다시 색칠한다.
(3) rotation 을 수행한다.

여기 (2) 단계에서 레드블랙트리의 구조가 망가질 수 있다. 새로운 노드를 레드로 만들면, 한 로우 내에 2개의 레드가 있을 수 없다는 규칙을 위반할 수 있고, 블랙으로 칠하면 root-null 경로의 블랙 노드의 수가 같아야 한다는 제약조건에 위배될 수 있다.

두 가지 경우중, 레드로 칠하는 경우가 더 가벼운 작업일 것 같으니

새로운 노드가 들어오면 먼저 레드로 칠해본다.

부모가 블랙이면 문제가 없다.

부모가 레드면?

몇 가지 경우를 생각해봐야 한다. 우선 부모 B 가 레드면, 부모의 부모 C 는 블랙임이 확실하다. 이 때 만약,

(1) C 가 B 말고 다른 자식 D 가 있다면 B, C, D 의 색을 반전시키면 된다. 그리고 새롭게 색을 반전시켰을 때 C 의 부모도 레드일 수 있다. 마찬가지로 recoloring 을 반복하면 된다. 색을 반전시켜도 (3) 또는 (4) 의 규칙을 위반하지 않는다.

아주 만약에, 루트까지 반복해서 루트가 레드가 되었다면 루트를 블랙으로 다시 칠하면 된다. 루트는 모든것의 부모이므로 블랙이 되어도 root-null 경로 조건을 위반하지 않는다.

따라서 연산비용은 O(log n) 이다.

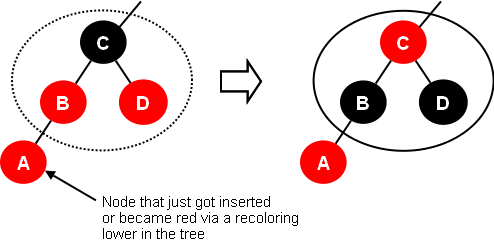
(http://cs.lmu.edu/~ray/notes/redblacktrees/)

그런데, 반복해서 이 방법을 사용하다가 C 가 다른 자식 D 를 가지고 있지 않거나, D 가 블랙일 수 있다. 그럴땐 다음 경우로 넘어가야 한다.

(2) C 가 B 말고 다른 자식이 없거나 블랙인 자식을 가지면 A 가 좌측이냐 우측이냐에 따라 right rotation, left-right rotation 으로 해결할 수 있다. 마찬가지로 (3) 또는 (4) 를 위반하지 않는다.

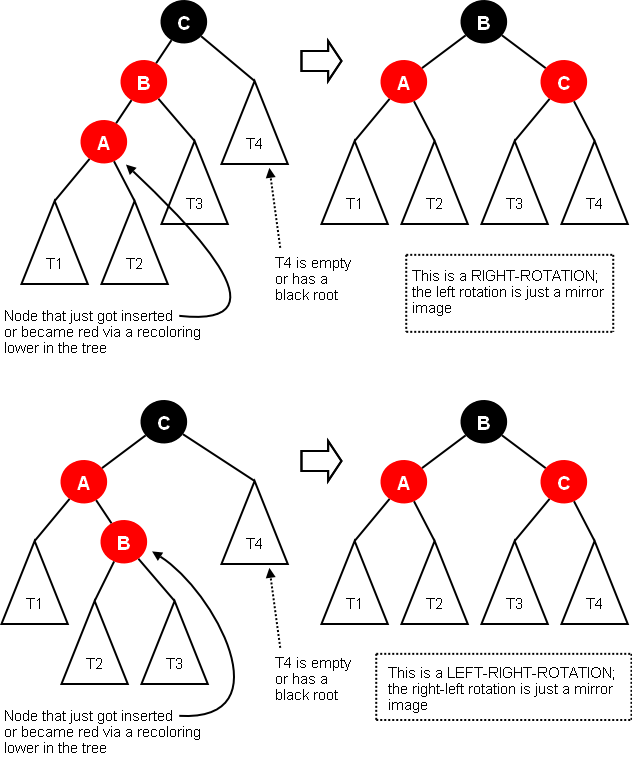
(http://cs.lmu.edu/~ray/notes/redblacktrees/)

이 경우는 몇번의 로테이션으로 해결할 수 있으므로 O(1) 이다.

References

(1) Algorithms: Design and Analysis, Part 1 by Tim Roughgarden
(2) Wiki - Binary heap
(3) Wiki - Binary search tree
(4) http://epaperpress.com
(5) http://commons.wikimedia.org/
(6) http://www.tcs.auckland.ac.nz/~georgy/
(7) Wiki - Red-black tree
(8) Wiki - Tree rotation