• linear programming: problem-solving model for optimal allocation of scarce resources, among a number of competing activities that encompasses

maxflow, MST, shortest paths, assigment, Ax = b, 2-person zero-sum games 등이 있다.

다시 말해서, constraints 를 지키면서 특정 값을 maximize 하는 문제다. 따라서 주어진 문제를 아래의 형태로 reduction 해야 한다.

(http://www.programering.com)

• fast commercial colvers available
• widely applicable problem-solving model
• key subroutine for integer programming solves

이므로 중요하다고 한다.

Brewer's Problem

양조장에서 맥주 ale, beer 를 생산하는데, 재료인 corn, hops malt 에 의해 생산량이 정해진다. 그리고 두 맥주는 들어가는 재료의 비율이 당연히 다르다.

이 때, 이익을 최대로 하는 각 맥주의 생산량을 구하는 문제다.

(http://www.programering.com)

위 그림처럼 contraints 를 그래프 문제로 변환할 수 있다. 이 때 이익을 최대로 하는 optimal solution 은 extreme point 에 위치하는데 이 점들은 2d 에선 2개의 constraints (선분) 이 교차하는 지점에 위치한다.

따라서

Goal maximize linear objective function of n nonnegative variables, subjet to m linear equations

문제를 standard form 으로 표시하면

• add variable Z and equation corresponding to objective function
• add slack variable to convert each inequality to an equality

Geometry

• Inequalities define halfspaces. feasible region is a convex polyhedron
• A set is convex if for any two points a and b in the set, so is 1/2(a+b)
• An extreme point of a set is a point in the set that can't be written as 1/2(a+b), where a and b are two distinct points in the set.

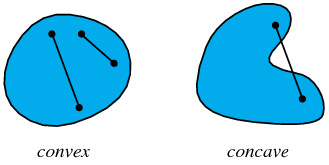
(http://mathworld.wolfram.com/Convex.html)

즉 두 점이 있을때 그 가운데 위치하는 점도 집합 안에 있으면 그 집합은 convex 라 부른다. extreme point 는 도형의 가장 바깥쪽 부분으로 그것보다 외부의 점이 없기 때문에 1/2(a+b) 로 바꿀 수 없다.

• Extreme point property:

If there exists an optimal solution to P (plane), then there exists one that is an extreme point

(1) Number of extreme points to consider is finite
(2) But number of extreme points can be exponential
(3) Extreme point optimal iff no better adjacent extreme point (greedy property)

특히 3번은 중요한데, global optimum 인지 알기 위해 인접부분만 검사하면 된다. 이는 objective function 이 선형이고, feasible region 이 convex 이기 때문이다.

Simplex Algorithm

1947년에 만들어진 알고리즘으로 20세기를 대표하는 탑 10 알고리즘중 하나라고 한다. generic algorithm 인데

• start at some extreme point
• Pivot from one extreme point to an adjacent one (never decreasing objective function)
• repeat until optimal

위에서 언급했던 greedy property 를 보면 이해가 쉽다. objective function 을 증가시키는 방향으로 extreme point 를 옮겨가다보면 global optimum을 찾을 수 있다.

Basic feasible solution

A basis is a subset of m of the n variables

• set n-m nonbasic variables to 0, solve for remaining m variables
• solve m equations in m unknowns
• if unique and feasible => BFS
• BFS <=> extream point

뭔소린가 한참을 쳐다봤는데, 그림으로 이해하는게 더 쉽다. n 개의 변수중 m 개를 제외한 것을 다 0 으로 하고, 방정식을 풀면 된다.

(http://www.programering.com)

slack variables 로 구성된 basis 부터 시작해서 pivot 연산을 해 나아가면 된다.

• use the variable whose coefficient in objective function is positive to replace some one in the basis (each unit increase in that variable from 0 increases objective value due to positive coefficient)

objective function 에서 계수가 양수인 수를 골라 치환하기 때문에 Z 값이 증가할수 밖에 없다.

• which variable to replace:

Preserves feasibility by ensuring RHS ≥ 0 and use minimum ratio rule: min { 480/15, 160/4, 1190/20 }

• when to stop: When no objective function coefficient is positive.

처음상태 basis = {SC, SH, SM} 에서 constraint B 를 B = (1/15)(450 - 5A - SC) 로 치환하면 B 가 SC 를 대신에 basis 에 들어간다.

(http://www.programering.com)

A 까지 치환하면 objective function 에 양수 계수를 가지는 변수가 없으므로 Z 가 더 증가할 여지가 없다.

Implementation

public class Simplex  
{
    private double[][] a; // simplex tableaux
    private int m, n; // M constraints, N variables

    public Simplex(double[][] A, double[] b, double[] c)
    {
        m = b.length;
        n = c.length;
        a = new double[m+1][m+n+1];
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                a[i][j] = A[i][j];
        for (int j = n; j < m + n; j++) a[j-n][j] = 1.0;
        for (int j = 0; j < n; j++) a[m][j] = c[j];
        for (int i = 0; i < m; i++) a[i][m+n] = b[i];
    }

    //Find entering column q using Bland's rule: index of first column whose objective function coefficient is positive.
    private int bland()
    {
        for (int q = 0; q < m + n; q++)
            if (a[M][q] > 0) return q;
                return -1;
    }

    //Find leaving row p using min ratio rule.
    private int minRatioRule(int q)
    {
        int p = -1;//leaving row
        for (int i = 0; i < m; i++)
        {
            if (a[i][q] <= 0) continue; //consider only positive entries
            else if (p == -1) p = i;
            else if (a[i][m+n] / a[i][q] < a[p][m+n] / a[p][q])
                p = i;
        }
        return p;
    }

    public void pivot(int p, int q)
    {
        for (int i = 0; i <= m; i++)
            for (int j = 0; j <= m+n; j++)
                if (i != p && j != q)
                    a[i][j] -= a[p][j] * a[i][q] / a[p][q];

        for (int i = 0; i <= m; i++)
            if (i != p) a[i][q] = 0.0;
        for (int j = 0; j <= m+n; j++)
            if (j != q) a[p][j] /= a[p][q];
        a[p][q] = 1.0;
    }

    public void solve()
    {
        while (true)
        {
            int q = bland();
            if (q == -1) break;//entering column q (optimal if -1)
            int p = minRatioRule(q);//leaving row p (unbounded if -1)
            if (p == -1) ...
            pivot(p, q);
        }
}

원본은 이리로 Simplex.java

메인 로직 자체는 간단하다.

(1) bland() 로 positive coefficient 인 변수를 찾고
(2) minRatioRule() 로 어떤 row 택할지 결정한다
(3) pivot

변수의 수를 N, 제약조건(= inequalities)의 수를 M 이라 했을때 M >= N 이면 러닝타임은 M^2 이다. 이는 pivot 연산이 대부분의 시간을 잡아먹기 때문.

근데 실제 돌려보면 2(M+N) pivot 내에 끝난다고 한다. 왜 그런지는 연구중이라고 함.

Pivoting rules: Carefully balance the cost of finding an entering variable with the number of pivots needed.

• No pivot rule is known that is guaranteed to be polynomial.

• Most pivot rules are known to be exponential (or worse) in worst-case.

Degeneracy

똑같은 extreme point 에 대해서 basis 만 바뀌는 것을 말하는데 위에서 본 bland's rule 이 작은 값부터 차례대로 사용 가능한 변수를 돌려주므로 유한한 수의 피벗이 일어남을 보장한다.

// Find entering column q using Bland's rule: 
// index of first column whose objective function coefficient is positive.
private int bland() {  
    for (int q = 0; q < m + n; q++)
        if (a[M][q] > 0) return q;
            return -1;
}

Implementation Issues

• Avoid stalling (degeneracy): requires artful engineering
• Maintain sparsity: requires fancy data structures
• Numerical stability: requires advances math
• Detect Infeasibility: run "phase i" simplex algorithm
• Detect unboundedness: no leaving row

그러므로 직접 구현하지 말자.. 사실 이해도 어렵다. 만드는 것은 둘째치고

Reductions

unrestricted variable B 가 있는 minimization 문제를 standard form 으로 reduction 하려면

(1) min(13A + 15B) 를 max(-13A - 15B) 로 변경
(2) 4A + 4B > 160 constraint 를 4A + 4B - S = 160 (S >= 0)
(3) B = B0 - B1 (B0 >= 0, B1 => 0)

Max Flow

capacity, flow 를 constraint 로 쉽게 바꿀 수 있다. 앞에서 본 max flow 알고리즘과 비교했을때의 장점은 문제가 더 복잡해지더라도 constraint 만 추가하면 간단하다는 점이다. (성능은 더 느릴수 있다고 함)

Bipartite Matching

여기서 X_ij 는 사람 i 에게 작업 j 가 할당되었는지의 여부다.

Summary

LP 가 범용적이긴 한데, 먼저 specialized algorithm 을 사용해 보고 안되면 LP 를 쓰자.

읽을거리: The real 10 algorithms that dominate our world

References

(1) Algorithms: Part 2 by Robert Sedgewick
(2) http://introcs.cs.princeton.edu
(3) getRandomNumber image
(4) Lecture note
(5) Mathword convex